Лекция 9. Современные технологии детекции изменений аналитических характеристик

М.И.Прищепа, кандидат технических наук, ЗАО «АНАЛИТИКА»

В настоящей лекции будут рассмотрены технологии мониторинга стабильности аналитических характеристик аналитических систем и методы детекции их изменений, которые были рекомендованы в последние десятилетия ведущими международными организациями и экспертами в области обеспечения качества лабораторных исследований. Главное внимание будет уделено аспектам надежности детекции этих изменений, а также вопросам их разграничения на существенные и несущественные.

В отличие от традиционных технологий, рассмотренных в Лекции 8, в современных подходах мониторинга стабильности аналитических характеристик (далее – АХ), используется понятие запаса по точности аналитической системы (далее – АС), а также показатели, характеризующие величину произошедших изменений ее АХ. Помимо этих понятий в современных технологиях получили широкое применение так называемые функции мощности детекции случаев изменения АХ, характеризующие вероятность отбраковки результатов исследований в проведенной серии в зависимости от величины изменения их аналитических ошибок. Использование перечисленных понятий и функций мощности дало возможность определять для конкретной АС оптимальную комбинацию из набора контрольных правил (далее – КП) и количества контрольных измерений (далее КИ) в серии, обеспечивающих заданную надежность детекции запредельных изменений АХ, а также разделять происходящие в них изменения на существенные и несущественные.

Итак, начнем с описания новых терминов, которые используются в современных технологиях мониторинга стабильности АХ. К таким терминам прежде всего относится вероятность отбраковки результатов аналитических серий, которую обычно обозначают как Р_r (r — от rejection). В узком смысле вероятность P_r определяют как вероятность того, что используемое КП при заданном числе КИ в серии выдаст сигнал на отбраковку проведенной аналитической серии [1]. Забегая вперед отметим, что при заданных КП и КИ в серии значение вероятности P_r зависит от величины изменения той или иной составляющей аналитической ошибки, то есть от величины изменения начальных значений систематического смещения или стандартной ошибки. При это следует также помнить, что КП, ввиду их статистической природы происхождения, могут выдавать сигналы на отбраковку серии не только в случаях изменения АХ, но и тогда, когда последние остаются стабильными в процессе эксплуатации АС.

Обычной реакцией на срабатывание КП является вполне естественное желание просто переделать текущую аналитическую серию еще раз. Как правило, так и поступают. Но такой вариант избавиться от возникшей проблемы ничего на самом деле не решает. И главным образом ввиду следующих двух причин. Так в случае, если серия была вполне удовлетворительной, а выдача сигнала на отбраковку серии является ложной из-за низких рабочих характеристик используемого КП, то тогда переделка текущей серии есть ненужное удвоение работы. Если же произошел реальный сбой в работе АС и она действительно вышла из-под контроля, то тогда тем более нецелесообразно повторно проводить серию, используя АС в таком ее состоянии, поскольку серия от этого лучше стать никак не сможет, а работа будет удвоена, не принося никакой пользы. Третьего тут не дано. Уместным решением этой проблемы является заблаговременный выбор для ведения оперативного контроля АС таких КП и КИ в серии, которые будут обеспечивать достаточно низкую вероятностью ложной отбраковки серий. Для таких случаев срабатывания КП алгоритм действий обычно следующий: приостановка эксплуатации АС, поиск неисправностей и их исправление, а также разработка по мере возможности превентивных мер по обеспечению бесперебойной работы АС. Повторять же серии по несколько раз в ожидании, что проблема сама собой рассосется, вряд ли имеет смысл.

Итак, в тех случаях, когда набор КП или используемое единичное правило срабатывает в отсутствие каких-либо изменений АХ, показатель Р_r по сути является вероятностью ложной отбраковки серии. Действительно, в таких случаях детектируется сбой в работе АС, которого на самом деле не было. Вероятность ложной отбраковки серий обычно обозначают как Р_fr (от false rejection). Значение показателя Р_fr дает оценку того, как часто при выбранных наборе КП и количестве КИ в серии будут отбраковываться аналитические серии при отсутствии изменений начальных значений АХ. То есть как часто будут подвергаться ложной отбраковке на самом деле очень хорошие аналитические серии. В идеале значение для вероятности Р_fr хотелось бы иметь равным 0%, но так не бывает. На практике для ведения оперативного контроля АС обычно выбирают такие наборы КП и такие количества КИ в серии, чтобы они могли обеспечивать вероятность Р_fr менее 5%. Как станет ясно дальше, вероятность ложной отбраковки Р_fr зависит не только от конкретного контрольного или предупредительного правила (далее – ПП), но и от количества КИ в серии. В Таблице 9.1 представлены значения показателя Р_fr для ряда КП и ПП при единичном КИ в серии. В Таблице 9.2 представлены значения показателя Р_fr для правила 1-2s при разном количестве КИ в серии. Как видно из первой таблицы, величину вероятности ложной отбраковки серий действительно можно значительно снижать, выбирая те или иные КП. Порой возникает потребность повысить эффективность детекции изменений АХ при использовании того же самого правила. Как станет ясно из дальнейшего, для этого необходимо увеличивать количество КИ в серии. В свою очередь, как это видно из Таблицы 9.2, увеличение КИ в серии приводит к увеличению показателя Р_fr для одного и того же правила.

Таблица 9.1. Вероятность ложной отбраковки Р_fr для разных контрольных правил при единичном контрольном измерении.

Контрольное/предупредительное правило	Вероятность ложной отбраковки Рfr,%
1-2s	4,55
1-2,5s	1,24
1-3s	0,27
1-3,5s	0,05
1-4s	0,01

Таблица 9.2. Вероятность ложной отбраковки Р_fr для предупредительного правила 1-2s в зависимости от числа контрольных измерений в аналитической серии.

Количество контрольных измерений	Вероятность ложной отбраковки Рfr для правила 1-2s, %
1	4,55
2	8,89
3	13,04
5	20,78
10	37,24
15	50,27
20	60,60

В тех случаях, когда КП срабатывает вследствие фактически произошедших изменений АХ, вероятность отбраковки Р_r называют вероятностью детекции ошибок и обозначают ее как Р_ed (от error detection). Значения показателя Р_ed показывают, как часто в процессе эксплуатации АС будут отбраковываться аналитические серии в зависимости от величины изменения АХ. В идеале значение показателя Р_ed хотелось бы иметь равным 100% для всех случаев запредельных изменений АХ, по крайней мере для случаев клинически значимых их изменений. Но так тоже не бывает. На практике для ведения оперативного контроля АС обычно подбирают такие КП и такие количества КИ в серии, чтобы показатель Р_ed имел значения не менее 90% для детекции случаев запредельных изменений АХ. Как станет видно из поведения функций мощности, о которых речь пойдет далее в этой лекции, значения показателя Р_ed, то есть вероятности детекции ошибок, для одного и того же КП зависят существенно от величины самого изменения АХ, то есть от величины изменения начальных значений смещения или стандартной ошибки АС.

Как показывает опыт, в процессе эксплуатации АС ее правильность и прецизионность обычно не изменяются одновременно. Обычно их изменения происходят с существенно разной частотой. Наиболее часто изменяется величина систематического смещения, главным образом из-за дрейфа калибровки. В любом случае изменения правильности и прецизионности АС в процессе ее эксплуатации можно разделить на существенные и несущественные. Если после произошедших изменений величины смещения и/или стандартной ошибки полная ошибка не превышает своего предельно допустимого значения (далее – ПДЗ), то такие изменения значений АХ следует считать несущественными. В том смысле, что такие изменения не требуют отбраковки результатов текущей серии. Действительно, если изменение значений АХ является несущественным, то есть оно не приводит к превышению полной ошибкой своего ПДЗ, тогда вполне логично полагать, что АС продолжает находиться под контролем и после произошедших изменений АХ. Поэтому важно уметь определять заранее предельно допустимые величины изменений отдельно для систематического смещения и отдельно для стандартной ошибки, еще не приводящие к превышению полной ошибкой своего ПДЗ. При условии, что соответственно прецизионность или правильность АС остаются стабильными. В этой связи в современных технологиях мониторинга стабильности АХ используют меру изменения и показатель запаса как для прецизионности, так и для правильности АС.

В качестве меры изменения случайной составляющей полной ошибки, то есть начального значения стандартной ошибки, обычно используют безразмерный показатель ∆RE, который показывает во сколько раз к настоящему моменту времени изменилось начальное значение стандартной ошибки S_ас. Так, если показатель ∆RE в какой-то момент эксплуатации АС оказывается равным 2, то это будет означать, что текущее значение стандартной ошибки S удвоилось по сравнению с ee начальным значением S_ac. Текущие значения показателя ∆RE вычисляют по формуле:

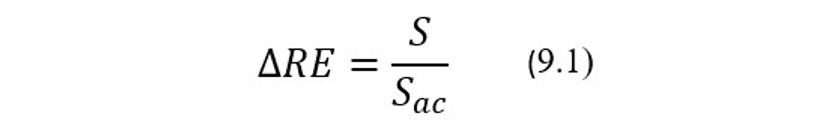
В качестве меры изменения систематической составляющей полной ошибки, т.е. начального значения систематического смещения, обычно используют безразмерный показатель ∆SE, который показывает на сколько начальных значений стандартной ошибки S_ас изменилось начальное значение систематического смещения В_ас. Так, если показатель ∆SE в какой-то момент эксплуатации АС оказывается равным 2, это будет означать, что текущее значение систематического смещения увеличилось на два S_ас по сравнению со своим начальным значением. Текущие значения показателя ∆SE вычисляются по формуле:

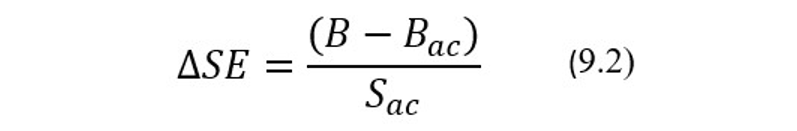
где B – текущее значение систематического смещения, а В_ас и S_ас – соответственно начальные значения систематического смещения и стандартной ошибки исследуемой АС.

Величину запаса по прецизионности принято оценивать безразмерным показателем критического изменения стандартной ошибки ∆RЕ_crit, который представляет собой максимально допустимое изменение текущей стандартной ошибки S в единицах ее начального значения S_ac, в условиях, когда начальное значение систематического смещения В_ас остается неизменным. Для таких условий максимальное допустимое значение стандартной ошибки S_crit = ∆RЕ_crit*S_ac (что следует из определения показателя ∆SЕ_crit) будет вычисляться по формуле:

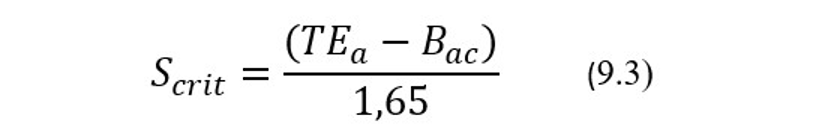
где ТЕ_а = B_ac+1,65*S_crit – предельно допускаемое значение для полной ошибки ТЕ_ас исследуемой АС в условиях стабильности ее правильности. Эксплуатационные значения ТЕ_ас вычисляют по известной формуле ТЕ_ас = В_ас+1,65*S_ас.

Исходя из вышесказанного, значения для показателя ∆RЕ_crit будут рассчитываться по формуле:

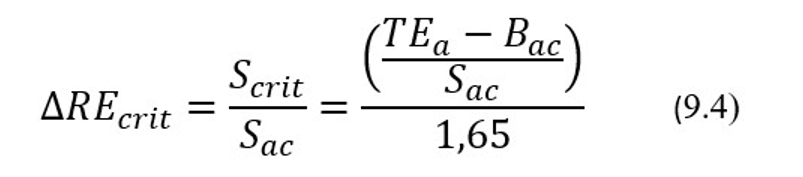
Так, например, если АС для определения содержания глюкозы в сыворотке вблизи 6 ммоль/л имеет начальные значения В_ас = 0,07 ммоль/л и S_ac = 0,08 ммоль /л, то тогда при TE_a = 0,36 ммоль/л [2] получим для ∆RЕ_crit следующее значение: ∆RЕ_crit = [(0,36-0,07)/0,08]/1,65 = 2,20. При округлении до целых значение ∆RЕ_crit будет равно 2. Таким образом для рассматриваемой АС в процессе ее эксплуатации допускается изменение начального значения показателя S_ac до 2 раз, т.е. вплоть до 0,16 ммоль/л. Соответственно в предположении стабильности начального значения В_ас систематического смещения АС. Тогда при достижении стандартной ошибкой своего предельно допускаемого значения, равного S_crit = 0,16 ммоль/л, значение полной ошибки ТЕ_ас будет равно 0,33 ммоль/л, что, из-за округления, оказалось чуть меньше ее предельно допускаемого значения ТЕ_а, равного 0,36 ммоль/л.

Величину запаса по правильности АС принято оценивать безразмерным показателем критического изменения систематического смещения ∆SЕ_crit, который представляет собой максимально допустимое изменение систематического смещения В_ас в единицах S_ac, в условиях, когда начальная прецизионность АС остается неизменной. Для таких условий максимальное допустимое значение систематического смещения будет равно B_crit = В_ac+∆SЕ_crit*S_ac, и, согласно определения показателя ∆SЕ_crit, будет вычисляться по формуле:

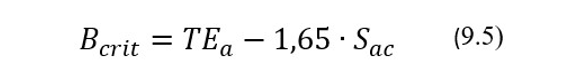
где ТЕ_а = B_crit+1,65*S_ac – предельно допускаемое значение для полной ошибки исследуемой АС в условиях стабильности ее прецизионности. Исходя из вышесказанного, значения показателя критического изменения смещения ∆SЕ_crit = (В_crit–B_ac)/S_ас с учетом формулы (9.5) будут рассчитываться по формуле:

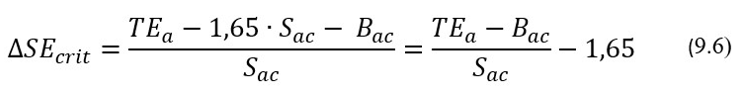
Так, например, если АС для определения содержания глюкозы в сыворотке вблизи 6 ммоль/л имеет изначальные значения В_ас = 0,07 ммоль/л и S_ac = 0,08 ммоль /л, то тогда при значении TE_a = 0,36 ммоль/л [2] получим для ∆SЕ_crit следующее значение: ∆SЕ_crit=[(0,36–0,07)/0,08]–1,65 = 1,98. При округлении до целых значение ∆SЕ_crit будет равно 2. Таким образом для такой АС в процессе ее эксплуатации допускается изменение начального значения смещения вплоть до двух начальных значений стандартной ошибки S_ас, то есть вплоть до 0,16 ммоль/л. При этом для предельного случая систематическое смещение B_crit будет равно 0,23 ммоль/л, а значение полной ошибки будет равно ТЕ_ас = (0,23+1,65*0,08) ммоль/л = 0,36 ммоль/л, то есть оно будет равно своему предельно допускаемому значению.

Теперь перейдем к рассмотрению понятия функции мощности. Оно имеет отношение к способу графического представления информации о рабочих характеристиках КП в виде значений вероятности отбраковки P_r, которые откладывают по оси ординат, в зависимости от величины изменения систематического смещения или стандартной ошибки, то есть в зависимости от показателей ∆SE или ∆RЕ, значения которых откладываются по оси абсцисс. Происхождение названия функции мощности имеет отношение к понятию статистической мощности в математической статистике. Из этого понятия следует, что чем больше мощность статистического теста, тем меньше вероятность совершить ошибку. В нашем случае, чем больше будет значение функции мощности, тем меньше будет вероятность пропустить произошедшее изменение АХ. Следует заметить, что значение вероятности ложной отбраковки P_fr определяется значением функции мощности, то есть значением вероятности отбраковки серий Р_r, при значении абсциссы ∆SЕ или ∆RЕ, равной нулю. Отметим также, что функции мощности зависят не только от конкретных КП или их набора, но и от количества КИ в серии.

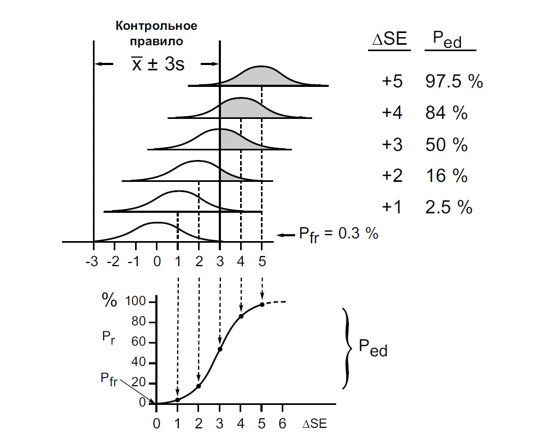
Рис. 9.1. Функция мощности детекции изменений систематического смещения для контрольного правила 1-3s. Ордината P_r соответствует вероятности P_ed, т.е. P_r = P_ed, везде, где абсцисса ∆SЕ>0, кроме точки ∆SЕ = 0, где P_r = P_fr.

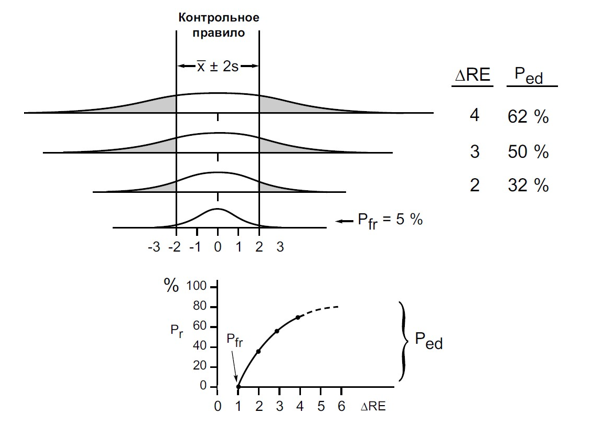
Рис. 9.2. Функция мощности детекции изменений стандартной ошибки для правила 1-2s. Ордината P_r соответствует вероятности P_ed, т.е. P_r = P_ed, везде, где абсцисса ∆SЕ>0, кроме точки ∆SЕ = 0, где P_r = P_fr.

Далее будет представлено в деталях построение графиков функции мощности детекции изменений соответственно систематического смещения и стандартной ошибки АС при использовании традиционных КП и ПП. Сначала рассмотрим самый простой случай, когда в аналитической серии проводится только одно КИ, пользуясь графическим подходом и пояснениями, изложенными в документе [3].

На Рис 9.1 проиллюстрирована зависимость функции мощности от положительного изменения систематического смещения для КП 1-3s. Предполагается, что величина стандартной ошибки в процессе эксплуатации АС сохраняется равной ее начальному значению S_ac. Отметим сразу же, что аналогичная ситуация будет наблюдаться и при отрицательных изменениях систематического смещения. Затемненные области указывают на величину вероятности отбраковки P_r, значения которой проецируются на расположенный ниже график функции мощности. Начальное значение показателя P_r, когда никаких изменений АХ нет и абсцисса в виде показателя ∆SЕ = 0, соответствует вероятности ложной отбраковки P_fr, в то время как вся остальная кривая описывает поведение вероятности детекции ошибки P_ed. Когда изменение начального значения систематического смещения превысит в 5 раз значение S_ac, т.е. когда показатель ∆SЕ станет равным 5 и более, тогда вероятность детекции ошибки P_ed превысит значение 97,5%. Это будет означать, что такое изменение систематического смещения вряд ли будет пропущено при использовании КП 1-3s с одним КИ в серии. А если и будет пропущено, то не чаще одного раза из 40 случаев. Другое дело, если потребуется надежно определять изменения систематического смещения меньшего размера, например в случаях, когда показатель ∆SЕ_crit для используемой АС оказывается равным 3 или даже меньше, что очень часто бывает на практике. Вероятность детекции ошибки в таких случаях будет меньше 50%. Т.е. каждое второе такое существенное изменение уже не будет определяться. В таких случаях, о чем речь пойдет далее, используют КП других типов и/или увеличивают число КИ в серии.

На Рис. 9.2 представлено поведение функции мощности в зависимости от изменения стандартной ошибки ∆RЕ для правила 1-2s. Как видно из рисунка, мощность детекции изменений стандартной ошибки при использовании данного правила значительно слабее в сравнении с предыдущим случаем детекции изменений систематического смещения. Даже в случае значительного изменения стандартной ошибки вероятность Р_ed весьма далека от 100%.

Таким образом видно, что мощности детектирования изменений смещения и стандартной ошибки существенно различаются, когда используется только одно КП и только одно КИ в серии. Причем величина вероятности ложной отбраковки P_fr определяется используемым контрольным или предупредительным правилом.

Для наглядного сравнения эффективности детекции изменений систематического смещения на Рис. 9.3, идея которого взята из документа [3], представлено несколько функций мощности соответственно для контрольных правил 1-2s, 1-3s и 1-4s. Для всех правил показатель предельно допустимого изменения систематического смещения ∆SЕ_crit предполагается равным 4. Как видно из этого рисунка, правила имеют вероятности ложной отбраковки P_fr, равные соответственно 5%, 0,3% и 0,01%, и вероятности детекции ошибки P_ed ри предельном значении изменении показателя ∆SЕ, равные соответственно 97,5%, 84% и 50%. Очевидно, что ни одно из представленных на рисунке правил не сочетает в себе обе вероятности оптимальным образом при значениях показателя ∆SЕ_crit, меньших 4.

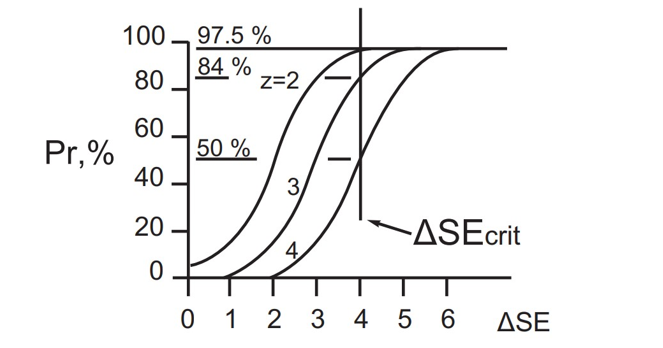
Рис. 9.3. Функции мощности детекции изменений систематического смещения для правил 1-2s, 1-3s и 1-4s в зависимости от величины изменения смещения ∆SЕ. Показатель предельно допустимого изменения систематического смещения ∆SЕ_crit предполагается равным 4 для всех правил. Соответствующие значения для вероятности ложной отбраковки Р_fr взяты из Таблицы 9.1.

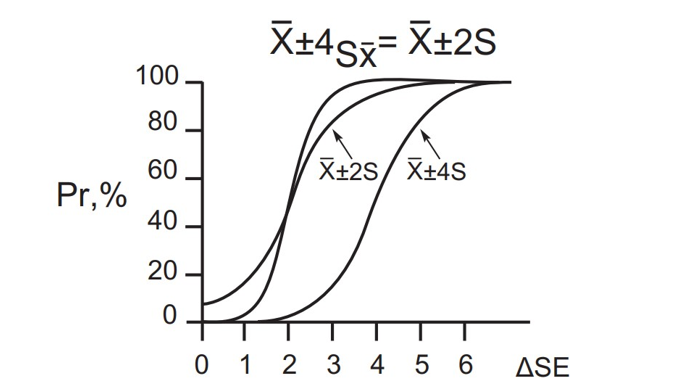
Рис. 9.4. Функции мощности детектирования изменений систематического смещения для КП 1-4s_х (4 репликаты) и для традиционных правил 1-2s, 1-4s в зависимости от величины изменения смещения ∆SЕ. Правило 1-4s_х построено на базе четырех репликат, сочетая в себе вероятность P_ed от правила 1-2s и вероятность P_fr от правила 1-4s.

Например, в случае АС, для которой показатель ∆SЕ_crit будет равен 3, вероятности P_fr для тех же правил будут оставаться прежними, а вот вероятности детекции ошибки P_ed будут ниже 90% и равны соответственно 84%, 50% и 16%. В случае АС, для которой показатель ∆SЕ_crit будет равен 2, вероятности P_ed для тех же правил окажутся еще меньше и составят только 50%, 16% и 2,5%. По этой причине современные технологии оперативного контроля АС не рекомендуют использовать традиционные КП в обособленном виде при одном КИ в серии. В таких случаях, как упоминалось выше, обычно рекомендуют либо увеличивать количество КИ в серии, либо использовать наборы традиционных КП, которые подбираются специальным образом, либо использовать КП на базе других статистик, например на базе средних по нескольким репликатам в серии или на базе экспоненциально взвешенных скользящих средних.

В качестве примера влияния на мощность детекции ошибок увеличенного количества КИ в серии на Рис. 9.4, идея которого взята также из документа [3], показана функция мощности для правила 1-4s_х, построенного на базе средних по четырем репликатам. В этом правиле в качестве контрольного результата (далее — КР) и его стандартной ошибки S_x используется соответственно среднее значение этих четырех репликат и стандартная ошибка этого среднего, которая будет в два раза меньше стандартной ошибки результата однократного измерения S, то есть S_x = S/2. Это обусловлено тем, что стандартная ошибка среднего значения по репликатам меньше стандартной ошибки результатов однократных измерений, то есть отдельных репликат, в корень квадратный из их числа. В данном случае в корень квадратный из 4, поскольку среднее значение вычисляется по четырем репликатам. Использование результатов четырех контрольных измерений позволяет при ∆SЕ_crit = 4 скомбинировать в правиле 1-4s_х низкое значение для P_fr, равное 0,01%, что во много раз меньше 5%, и высокое значение для P_ed, равное 97,5%, что значительно больше 90%. Однако использование этого правила в случаях, когда показатель ∆SЕ_crit = 2, позволяет обеспечивать значение для P_ed, равное только 50%, что явно меньше обычно требуемых 90%. Поэтому для тех случаев, когда показатель ∆SЕ_crit = 2 или около того, необходимо искать другие решения. Современные технологии в таких случаях обычно рекомендуют не только увеличивать число КИ в серии, но также использовать либо наборы традиционных КП, либо КП на базе других статистик.

Помимо традиционных КП и правил на основе средних по репликатам, в современных технологиях мониторинга стабильности АХ широко начали использоваться КП на основе так называемых экспоненциально взвешенных скользящих средних [4]. В англоязычном варианте эта статистика имеет название Exponentially Weighted Moving Average (далее – EWMA). Впервые ее понятие ввел Робертс [5] еще в 1959 году. Текущее значение EWMA получают усреднением двух его предыдущих значений, причем усреднение проводится таким образом, чтобы последнее из усредняемых значений оказывало все меньшее и меньшее влияние на последующие результаты усреднения. Статистика на основе экспоненциально взвешенной скользящей средней (далее – статистика EWMA) обычно используется для мониторинга стабильности процессов, где важно отслеживать небольшие или постепенные изменения контролируемого параметра, обусловленные медленным уходом его последующих значений от первоначального. Например, медленное изменение начального значения систематического смещения АС вследствие дрейфа калибровочной зависимости. Отметим, что в отличие от статистики EWMA при использовании традиционных КП решение о состоянии стабильности АХ в любой момент времени зависит только от самых последних результатов КИ, от точности определения первоначальных значений АХ и от устанавливаемых контрольных границ. В статистике на основе EWMA такое решение зависит от экспоненциально взвешенного скользящего среднего, которое, как станет ясно дальше, определяется на основе всех результатов КИ, полученных в процессе ведения мониторинга (включая результаты самых последних измерений). Как будет показано далее, путем подбора соответствующего значения для так называемой сглаживающей константы λ оперативный контроль АС на основе статистики EWMA может быть сделан весьма чувствительным к небольшим изменениям систематического смещения, в то время как традиционные КП срабатывают только в случае выхода последнего КР за установленные границы.

Чтобы лучше понимать за счет чего можно регулировать чувствительность КП на основе статистики EWMA к величине изменения систематического смещения, рассмотрим, каким образом строятся и работают эти правила. Значение экспоненциально взвешенного скользящего среднего Y_i, соответствующего контрольному результату X_i рассчитывают по следующей формуле:

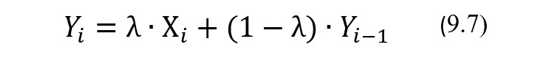
где индекс i принимает значения i =1, 2,…, n, а значение Y₀ = Х_ср, то есть представляет собой среднее значение результатов контрольных измерений, полученных в установочной серии, X_i – i-тый по счету КР, полученный в процессе ведения оперативного контроля, n – число КР, полученных при ведении оперативного контроля, включая Y_0, λ – сглаживающая константа, которая может принимать значения от 0 и до 1, точнее 0<λ≤1.

По своей сути сглаживающая константа λ определяет статистический вес вклада предыдущих значений в текущее вычисляемое значение экспоненциально взвешенного скользящего среднего. Как видно из формулы (9.7), чем ближе ее значение к 0, тем сильнее влияние «более старых» значений экспоненциально взвешенного скользящего среднего на последующие. И наоборот. Например, если выбрать для λ значение, равное 1, то это будет приводить к тому, что текущее значение экспоненциально взвешенного скользящего среднего будет целиком определяться только самым последним КР. Фактически это будет означать, что статистика EWMA при значении λ = 1 вырождается в статистику, используемую в традиционных КП. Таким образом, значения λ, близкие к 1, будут давать больше веса последним данным и меньше веса «более старым». Соответственно, значения λ, близкие к 0, будут давать больше веса более «старым данным». Обычно принято, как это следует из работы [6], для константы λ выбирать значения между 0,2 и 0,3, хотя в таком выборе есть доля некоторого произвола. Поэтому достаточно часто рекомендуют обращаться к работе [7], в которой приводятся таблицы, предоставляющие возможность выбирать значения для λ более обоснованно.

Для построения контрольных карт в статистике EWMA помимо начального значения экспоненциально взвешенного скользящего среднего Y₀ необходимо также уметь вычислять его дисперсию. Для контрольных результатов с индексом i свыше 7 дисперсию экспоненциально взвешенного скользящего среднего (S_Y)² можно приблизительно вычислять по нижеследующей достаточно простой формуле [8]:

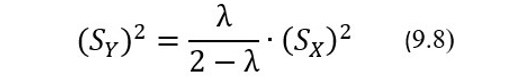
где (S_Y)² – дисперсия экспоненциально взвешенного скользящего среднего, (S_Х)² – дисперсиярезультатов КИ, а S_X – их стандартное отклонение, λ – сглаживающая константа, принимающая значения от 0 и до 1. Соответственно верхняя Y_ВКГ и нижняя Y_НКГ контрольные границы для контрольных карт статистики EWMA для экспоненциально взвешенного скользящего средних с индексом i≥7 можно вычислять по формулам:

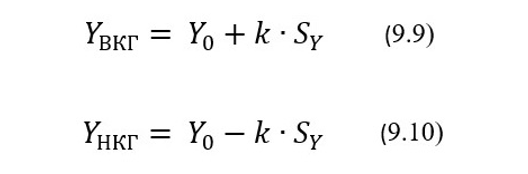
где k – коэффициент, значение которого зависит от используемого контрольного правила. Так при использовании контрольного правила EWMA2S_Y, которое срабатывает в случае отклонения значения Y_i от Y₀ свыше двух S_y, коэффициент k выбирают равным 2, и соответственно при использовании контрольного правила EWMA3S_Y, которое срабатывает в случае отклонения значения Y_i от Y₀ свыше трех S_y, коэффициент k выбирают равным 3.

В качестве примера предположим, что по итогам проведения установочной серии на гемоглобинометре, вводимом в эксплуатацию, были получены следующие оценочные значения, используемые обычно для построения контрольных карт: Хср = 140 г/л и S_X = 2 г/л. Тогда для начального значения экспоненциально взвешенного скользящего среднего будем иметь Y₀ = Хср =140 г/л. Также положим коэффициент k равным 3, а константу λ равной 0,3. Воспользуемся формулами (9.8) – (9.10) и получим значение для стандартного отклонения в статистике EWMA S_Y = 0,84 г/л и соответственно значения для верхней границы Y_ВКГ = 142,52 г/л и для нижней границы Y_НКГ = 137,48 г/л. Контрольные карты в статистике EWMA строят по тому же алгоритму, что и в статистике Шухарта/Леви-Дженнингса: проводят горизонтальную линию Y₀ и параллельно ей линии Y₀±1*S_Y, Y₀±2*S_Y и Y₀ ±3*S_Y, по оси ординат откладываются значения Y_i, а по оси абсцисс – значения индекса i в качестве номеров контрольных результатов.

Как станет ясно из дальнейшего сравнения различных КП, правила на основе статистики EWMA обладают, по сравнению с традиционными правилами, существенно большей мощностью детекции «поломок» АС с низким запасом прочности по систематическому смещению. Здесь же отметим, что величина показателя P_fr для правил на основе статистики EWMA, как это видно из Рис. 9.5, зависит от величины сглаживающей константы λ.

Рис. 9.5. Зависимость показателя P_fr для КП на основе статистики EWMA от величины сглаживающей константы λ. Для правила, обозначенного как EWMA2S-0,3, предполагается, что коэффициент k=2 (см. формулы (9.9) и (9.10)), а сглаживающая константа λ=0,3. Показатель ∆SE_min определяет величину изменения начального систематического смещения, при котором P_ed = 90%.

Помимо КП на основе статистики EWMA повышенной чувствительностью к небольшим изменениям систематического смещения АС обладает также КП на основе критерия Колмогорова, предложенное в 2018 году сотрудником ЗАО «АНАЛИТИКА» Иваном Васильевым. Алгоритм работы КП на основе критерия согласия Колмогорова в принципе такой же, как и у других КП. Он состоит в проверке на выбираемом уровне значимости нулевой гипотезы о принадлежности выборки КР закону их распределения в генеральной совокупности, то есть по сути в проверке того, что эмпирическое распределение соответствует его предполагаемой модели. Распределение КР в генеральной совокупности предполагается нормальным с параметрами, которые рассчитываются на основе данных установочной серии. И если этот критерий согласия не выполняется, то нулевая гипотеза и КП считаются нарушенными. Проверка нулевой гипотезы на основе критерия Колмогорова проводится путем сравнения статистики D_n Колмогорова с ее предельно допустимым значением D_n(α), которое в свою очередь зависит от объема выборки n и выбираемого уровня значимости α, соответствующего вероятности ложноположительных результатов. Уровень значимости α обычно выбирают равным 5%. Значения статистики D_n Колмогорова рассчитывают по формуле:

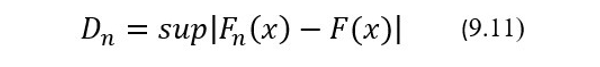
Здесь понятие супремума sup (сокращенно от supremum) означает точную верхнюю границу множества соответствующих разностей |F_n(x)–F(x)|. Соответственно, F_n(x) – это эмпирическая функция распределения, описанная Колмогоровым, а F(x) – это теоретическая функция распределения случайной величины х. Если окажется, что D_n>D_n(α), это будет означать, что произошло практически невероятное событие. В таком случае нулевая гипотеза отклоняется, а КП считается нарушенным на уровне значимости α. При этом вероятность ошибочного отклонения на самом деле верной гипотезы не превышает принятый уровень значимости α. Поскольку в рассматриваемом случае теоретическое распределение КР предполагается нормальным, то значения теоретической функции распределения F(x) случайной величины x c математическим ожиданием µ и дисперсией σ² вычисляют по формуле:

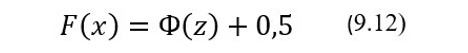
где Ф(z) = Ф[(х-µ)/σ] – известная интегральная функция Лапласа, некоторые значения которой приведены в Таблице 9.3. Что касается эмпирической функции распределения F_n(x) случайной величины х, представленной выборкой х₁, х₂,…, х_n, то ее значения рассчитываются по формуле:

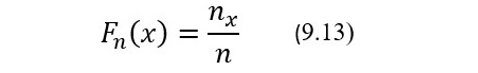
где n_x – количество элементов выборки, значения которых меньше значения х, а n – объем выборки. Как видно из формулы (9.13), эмпирическая функция распределения F_n(x) определяет для каждого х частоту появления элементов выборки, значения которых меньше или равны х. Отличие эмпирической функции распределения от теоретической состоит в том, что последняя определяет не частоту, а вероятность появления значений случайной величины х, меньших или равных х. Если элементы полученной выборки проранжировать так, чтобы выполнялось условие х_1≤х_2≤…≤x_n-1≤х_n, то тогда очевидно, что для всех х<х₁ значения F_n(x) будут равны 0, поскольку n_x = 0, а для всех х≥х_n значения F_n(x) будут равны 1, поскольку n_x = n. Также очевидно, что по мере увеличения числа элементов (то есть числа КР) в получаемых выборках, разница |F_n(x)–F(x)| будет стремиться к 0, если элементы полученных выборок будут принадлежать одной и той же генеральной совокупности. Если этого не будет происходить, то это будет означать, что параметры распределения КР в их генеральной совокупности изменились в какой-то момент времени наблюдения за стабильностью АХ АС.

Для приближенного расчета значений D_n = sup |F_n(x)–F(x)| на практике обычно используют формулу (9.14), вытекающую из формул (9.11) и (9.13):

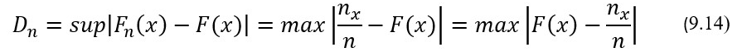
Как упоминалось выше, критические значения D_n(α) зависят от объема выборки n и выбираемого уровня доверия α. Эти критические значения для статистики Колмогорова либо вычисляют самостоятельно, либо берут из соответствующих справочников, наиболее известным из которых является справочник [9]. Некоторые критические значения для статистики Колмогорова из этого справочника приведены в Таблице 9.4, где n – объем рассматриваемой выборки контрольных результатов, а α – уровень значимости. В случае необходимости при n≥10 и выборе уровня значимости α от 1% до 20% критические значения D_n(α) c достаточно высокой точностью можно рассчитывать по следующей формуле:

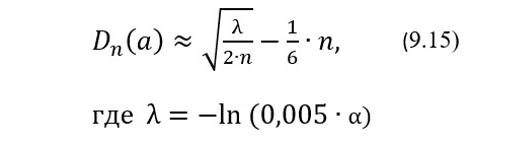
Таблица 9.3. Таблица значений интегральной функции Лапласа Ф(z).

z            Ф(z)          z           Ф(z)         z          Ф(z)          z           Ф(z)          z            Ф(z)        z          Ф(z)   .        0,00      0,0000      0,50      0,1915      1,00      0,3413     1,50      0,4332     2,00      0,4772     3,00     0,498650   0,01      0,0040      0,51      0,1950      1,01      0,3438     1,51      0,4345     2,02      0,4783     3,20     0,499310 0,02      0,0080      0,52      0,1985      1,02      0,3461     1,52      0,4357     2,04      0,4793     3,40     0,499660 0,03      0,0120      0,53      0,2019      1,03      0,3485     1,53      0,4370     2,06      0,4803     3,60     0,499841 0,04      0,0160      0,54      0,2054      1,04      0,3508     1,54      0,4382     2,08      0,4812     3,80     0,499928 0,05      0,0199      0,55      0,2088      1,05      0,3531     1,55      0,4394     2,10      0,4821     4,00     0,499968 0,06      0,0239      0,56      0,2123      1,06      0,3554     1,56      0,4406     2,12      0,4830     4,50     0,499997 0,07      0,0279      0,57      0,2157      1,07      0,3577     1,57      0,4418     2,14      0,4838     5,00     0,499997 0,08      0,0319      0,58      0,2190      1,08      0,3599     1,58      0,4429     2,16      0,4846                               . 0,09      0,0359      0,59      0,2224      1,09      0,3621     1,59      0,4441     2,18      0,4854                               .                          0,10      0,0398      0,60      0,2257      1,10      0,3643     1,60      0,4452     2,20      0,4861                               . 0,11      0,0438      0,61      0,2291      1,11      0,3665     1,61      0,4463     2,22      0,4868                               . 0,12      0,0478      0,62      0,2324      1,12      0,3686     1,62      0,4474     2,24      0,4875                               . 0,13      0,0517      0,63      0,2357      1,13      0,3708     1,63      0,4484     2,26      0,4881                               . 0,14      0,0557      0,64      0,2389      1,14      0,3729     1,64      0,4495     2,28      0,4887                               . 0,15      0,0596      0,65      0,2422      1,15      0,3749     1,65      0,4505     2,30      0,4893                               . 0,16      0,0636      0,66      0,2454      1,16      0,3770     1,66      0,4515     2,32      0,4898                               . 0,17      0,0675      0,67      0,2486      1,17      0,3790     1,67      0,4525     2,34      0,4904                               . 0,18      0,0714      0,68      0,2517      1,18      0,3810     1,68      0,4535     2,36      0,4909                               . 0,19      0,0753      0,69      0,2549      1,19      0,3830     1,69      0,4545     2,38      0,4913                               . 0,20      0,0793      0,70      0,2580      1,20      0,3849     1,70      0,4554     2,40      0,4918                               . 0,21      0,0832      0,71      0,2611      1,21      0,3869     1,71      0,4564     2,42      0,4922                            . 0,22      0,0871      0,72      0,2642      1,22      0,3883     1,72      0,4573     2,44      0,4927                               . 0,23      0,0910      0,73      0,2673      1,23      0,3907     1,73      0,4582     2,46      0,4931                               . 0,24      0,0948      0,74      0,2703      1,24      0,3925     1,74      0,4591     2,48      0,4934                               . 0,25      0,0987      0,75      0,2734      1,25      0,3944     1,75      0,4599     2,50      0,4938                               . 0,26      0,1026      0,76      0,2764      1,26      0,3962     1,76      0,4608     2,52      0,4941                               . 0,27      0,1064      0,77      0,2794      1,27      0,3980     1,77      0,4616     2,54      0,4945                               . 0,28      0,1103      0,78      0,2823      1,28      0,3997     1,78      0,4625     2,56      0,4948                               . 0,29      0,1141      0,79      0,2852      1,29      0,4015     1,79      0,4633     2,58      0,4951                               . 0,30      0,1179      0,80      0,2881      1,30      0,4032     1,80      0,4641     2,60      0,4953                                . 0,31      0,1217      0,81      0,2910      1,31      0,4049     1,81      0,4649     2,62      0,4956                               . 0,32      0,1255      0,82      0,2939      1,32      0,4066     1,82      0,4656     2,64      0,4959                               . 0,33      0,1293      0,83      0,2967      1,33      0,4082     1,83      0,4664     2,66      0,4961                               . 0,34      0,1331      0,84      0,2995      1,34      0,4099     1,84      0,4671     2,68      0,4963                                . 0,35      0,1368      0,85      0,3023      1,35      0,4115     1,85      0,4678     2,70      0,4965                               .  0,36      0,1406      0,86      0,3051      1,36      0,4131     1,86      0,4686     2,72      0,4967                               .    0,37      0,1443      0,87      0,3078      1,37      0,4147     1,87      0,4693     2,74      0,4969                               .      0,38      0,1480      0,88      0,3106      1,38      0,4162     1,88      0,4699    2,76      0,4971                               .    0,39      0,1517      0,89      0,3133      1,39      0,4177     1,89      0,4706     2,78      0,4973                               .        0,40      0,1554      0,90      0,3159      1,40      0,4192     1,90      0,4713     2,80      0,4974                                .          0,41      0,1591      0,91      0,3186      1,41      0,4207     1,91      0,4719     2,82      0,4976                                .                     0,42      0,1628      0,92      0,3212      1,42      0,4222     1,92      0,4726     2,84      0,4977                                .                         0,43      0,1664      0,93      0,3238      1,43      0,4236     1,93      0,4732     2,86      0,4979                               . 0,44      0,1700      0,94      0,3264      1,44      0,4251     1,94      0,4738     2,88      0,4980                               . 0,45      0,1736      0,95      0,3289      1,45      0,4265     1,95      0,4744     2,90      0,4981                               . 0,46      0,1772      0,96      0,3315      1,46      0,4279     1,96      0,4750     2,92      0,4982                               .    0,47      0,1808      0,97      0,3340      1,47      0,4292     1,97      0,4756     2,94      0,4984                               .  0,48      0,1844      0,98      0,3365      1,48      0,4306     1,98      0,4761     2,96      0,4985                               . 0,49      0,1879      0,99      0,3389      1,49      0,4319     1,99      0,4767     2,98      0,4986                               .

Таблица 9.4. Критические значения для наибольших отклонений эмпирического распределения от теоретического (критерий Колмогорова).

n/a	10%	5%	1%	n/a	10%	5%	1%
1	0,95000	0,97500	0,99500	41	0,18687	0,20760	0,24904
2	0,77639	0,84189	0,92929	42	0,18468	0,20517	0,24613
3	0,63604	0,70760	0,82900	43	0,18257	0,20283	0,24332
4	0,56522	0,62394	0,73424	44	0,18053	0,20056	0,24060
5	0,50945	0,56328	0,66853	45	0,17856	0,19837	0,23798
6	0,46799	0,51926	0,61661	46	0,17665	0,19625	0,23544
7	0,43607	0,48342	0,57581	47	0,17481	0,19420	0,23298
8	0.40962	0,45427	0,54179	48	0,17302	0,19221	0,23059
9	0,38746	0,43001	0,51332	49	0,17128	0,19028	0,22828
10	0,36866	0,40925	0,48893	50	0,16959	0,18841	0,22604
11	0,35242	0,39122	0,46770	51	0,16796	0,18659	0,22386
12	0,33815	0,37543	0,44905	52	0,16637	0,18482	0,22174
13	0,32549	0,36143	0,43247	53	0,16483	0,18311	0,21968
14	0,31417	0,34890	0,41762	54	0,16332	0,18144	0,21768
15	0,30397	0,33760	0,40420	55	0,16186	0,17981	0,21574
16	0,29472	0,32733	0,39201	56	0,16044	0,17823	0,21384
17	0,28627	0,31796	0,38086	57	0,15906	0,17669	0,21199
18	0,27851	0,30936	0,37062	58	0,15771	0,17519	0,21019
19	0,27136	0,30143	0,36117	59	0,15639	0,17373	0,20844
20	0,26473	0,29408	0,35241	60	0,15511	0,17231	0,20673
21	0,25858	0,28724	0,34427	61	0,15385	0,17091	0,20506
22	0,25283	0,28087	0,33666	62	0,15263	0,16956	0,20343
23	0,24746	0,27490	0,32954	63	0,15144	0,16823	0,20184
24	0,24242	0,26931	0,32286	64	0,15027	0,16693	0,20029
25	0,23768	0,26404	0,31657	65	0,14913	0,16567	0,19877
26	0,23320	0,25907	0,31064	66	0,14802	0,16443	0,19729
27	0,22898	0,25438	0,30502	67	0,14693	0,16322	0,19584
28	0,22497	0,24993	0,29971	68	0,14587	0,16204	0,19442
29	0,22117	0,24571	0,29466	69	0,14483	0,16088	0,19303
30	0,21756	0,24170	0,28987	70	0,14381	0,15975	0,19167
31	0,21412	0,23788	0,28530	71	0,14281	0,15864	0,19034
32	0,21085	0,23424	0,28094	72	0,14183	0,15755	0,18903
33	0,20771	0,23076	0,27677	73	0,14087	0,15649	0,18776
34	0,20472	0,22473	0,27279	74	0,13993	0,15544	0,18650
35	0,20185	0,22425	0,26897	75	0,13901	0,15442	0,18528
36	0,19910	0,22119	0,26532	76	0,13811	0,15342	0,18408
37	0,19646	0,21826	0,26180	77	0,13723	0,15244	0,18290
38	0,19392	0,21544	0,25843	78	0,13636	0,15147	0,18174
39	0,19148	0,21273	0,25518	79	0,13551	0,15052	0,18060
40	0,18913	0,21012	0,25205	80	0,13467	0,14960	0,17949

В качестве примера использования критерия Колмогорова проверим на уровне значимости α = 5% нулевую гипотезу о принадлежности выборки КР нормальному закону их распределения в генеральной совокупности с параметрами µ = 100 г/л, σ = 3 г/л. В качестве выборки КР возьмем, например, 10 проранжированных результатов КИ уровня аналита в аликвотах одного и того же контрольного материала, которые были получены в нескольких последовательно проведенных аналитических сериях и которые обозначим как х_i (i = 1, 2,…, n): 93, 95, 97, 98,100, 101, 102, 104, 106 и 109 г/л. Результаты расчетов сведем в Таблицу 9.5. Поскольку интегральная функция Лапласа нечетная, будем иметь ввиду, что Ф(–z) = –Ф(z). Значения для Ф(z) и D_n(α) будем выбирать из Таблиц 9.3 и 9.4. Значения для D_n будем вычислять по формуле (9.14).

Таблица 9.5. Пример использования критерия Колмогорова.

Номер КР, i	Значе-ние КР(xi)	Fn(x) =nx/n	z(x-µ)/σ	Ф(z)	F(x) = Ф(z) +0,5	|Fn(x)–F(x)|	D10	D10(α)
1	94	0,1	–2,000	–0,477	0,023	0,077
2	97	0,2	–1,000	–0,341	0,159	0,041
3	99	0,3	–0,333	–0,131	0,369	0,069
4	105	0,4	1,667	0,452	0,952	0,552
5	106	0,5	2,000	0,477	0,977	0,477
6	107	0,6	2,333	0,490	0,990	0,390
7	108	0,7	2,667	0,496	0,996	0,296
8	109	0,8	3,000	0,499	0,999	0,199
9	110	0,9	3,333	0,499	0,999	0,099
10	112	1,0	4,000	0,500	1,000	0,000
							0,552	0,409

Так как D₁₀ = 0,552, что больше его критического значения D₁₀(α) = 0,409, то соответственно на 5% уровне значимости нулевая гипотезы о принадлежности выборки КР закону их теоретического распределения в генеральной совокупности отвергается. Это обуславливает срабатывание КП на основе критерия Колмогорова, что подтверждает, что исследуемая АС вышла из под контроля при проведении одной из рассматриваемых серий, скорее всего в той из них, в которой был получен КР с индексом i = 4 или КР с индексом i = 5.

На Рис. 9.6 и 9.7 представлены графики функций мощности детекции изменений систематического смещения типовой АС, предназначенной для определения концентрации эритроцитов в крови, различными наборами КП, в том числе на основе статистики EWMA и статистики Колмогорова. По своей сути, как упоминалось выше, такие графики функций мощности от систематического смещения определяют вероятности отбраковки аналитических серий различными наборами КП в зависимости от величины изменения ∆SЕ начального систематического смещения. На каждом из двух рисунков рассматривается типовая АС для определения концентрации эритроцитов в крови, для которой после проведения установочной серии были получены следующие значения: Х_ср = 4,48·10¹²/л, относительное систематическое смещение В_ас,% = 0,08%, коэффициент вариации CV_ас = 0,96%. Согласно [2] для такого аналита предельно допускаемые значения для коэффициента вариации CV_а = 1,6%, для относительного смещения В_а,% = 1,7%, для полной ошибки ТЕ_а(%) = В_а,%+1,65*CVа = 4,34%. Тогда, используя в формуле (9.6) перечисленные выше значения, получим для ∆SЕ_crit = [(4,34–0,08)/0,96]–1,65 = 2,79.

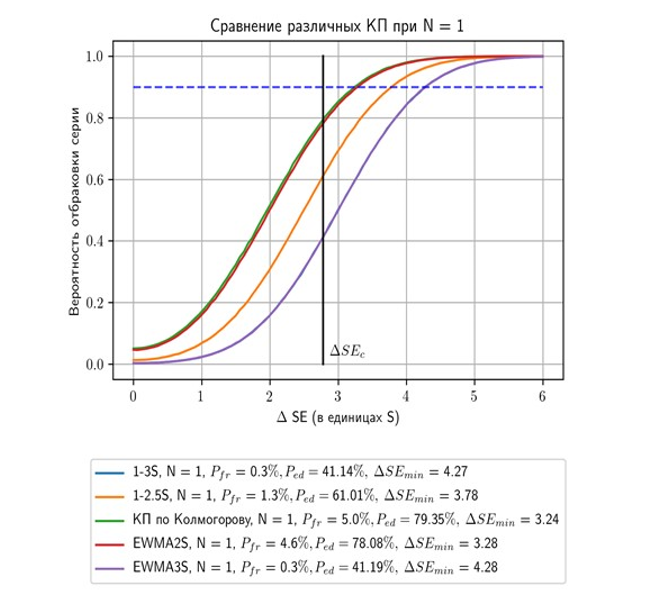
Рис. 9.6. Сравнение функций мощности детекции изменений систематического смещения АС, предназначенной для определения концентрации эритроцитов в крови, с использованием различных КП. Графики функций мощности для правил 1-3s и EWMA3S практически совпадают. Сглаживающая константа λ = 0,5 для всех КП на основе статистики EWMA. Количество КИ в каждой аналитической серии N = 1. Показатель критического изменения систематического смещения ∆SЕ_crit(∆SЕ_c) равен 2,79. Показатель ∆SЕ_min – это изменение систематического смещения АС в единицах начальной стандартной ошибки S, вероятность детекции которого равна 90%.

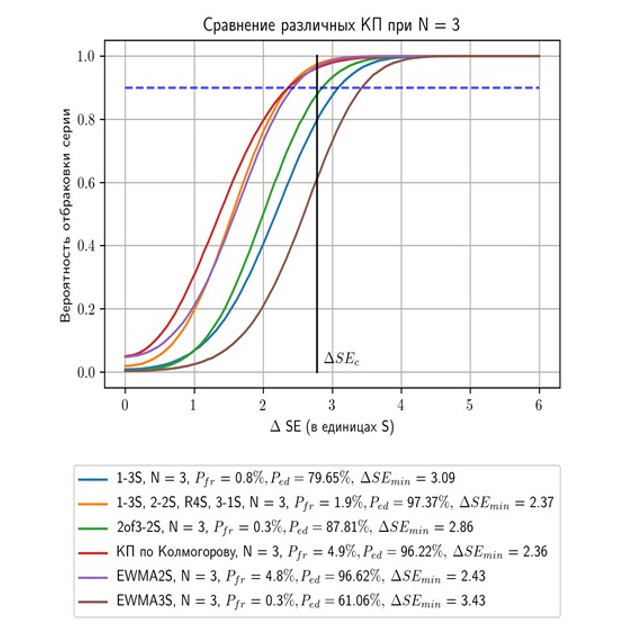
Рис. 9.7. Сравнение функций мощности детекции изменений систематического смещения АС, предназначенной для определения концентрации эритроцитов в крови, с использованием различных КП. Сглаживающая константа λ=0,5 для всех КП на основе статистики EWMA. Количество КИ в каждой аналитической серии N=3. Показатель критического изменения систематического смещения ∆SЕ_crit(∆SЕ_c) равен 2,79. Показатель ∆SЕ_min – это изменение систематического смещения АС в единицах начальной стандартной ошибки S, вероятность детекции которого равна 90%.

Напомним, что для того, чтобы тот или иной набор КП соответствовал международным требованиям к качеству детекции случаев выхода АС из-под контроля, достаточно выполнения следующих условий: показатель P_fr≤5%, а показатель P_ed≥90% при величине изменения начального смещения ∆SЕ = ∆SЕ_crit. Как видно из рисунков выше, для всех наборов КП вероятность отбраковки аналитической серии увеличивается при увеличении показателя ∆SЕ, т.е. по мере возрастания систематического смещения АС. Значит для того, чтобы тот или иной набор КП соответствовал международным требованиям, достаточно выполнения следующих условий: P_fr≤5% и ∆SЕ_min≤∆SЕ_crit. Показатель ∆SЕ_min – это изменение систематического смещения АС в единицах начальной стандартной ошибки S_ac, вероятность детекции которого конкретным набором КП равна 90%. Величина ∆SЕ_min для конкретного набора КП на графиках определяется точкой пересечения искомой функции мощности с горизонтальной прямой, соответствующей уровню вероятности отбраковки серии, равному 0,9 (или 90%, что тоже самое).

Как видно из Рис. 9.6, если количество КИ в каждой аналитической серии N только одно (N = 1), то ни один из рассматриваемых наборов КП не может с требуемой вероятностью выявлять случаи предельного изменения систематического смещения, так как ни для одного из рассматриваемых наборов КП условие ∆SЕ_min≤∆SЕ_crit не выполняется. Это означает, что с одним КИ в серии с помощью рассматриваемых наборов КП требуемого уровня качества детекции предельных изменений смещения рассматриваемой АС достичь нельзя, что вынуждает увеличивать количество КИ в серии.

На Рис. 9.7 рассматривается вариант с увеличением количества КИ в каждой аналитической серии до трех (N = 3). Как видно из этого рисунка, при использовании некоторых наборов КП из одного правила, таких как 1-3s, 2of3_2s (два из трех подряд КР выходят за Х_ср+2S или за Х_ср–2S) и EWMA3s даже с тремя КИ в серии не обеспечивают нужных требований, так как для них условие ∆SЕ_min≤∆SЕ_crit не выполняется. В тоже время КП по Колмогорову, КП на основе EWMA2s и набор из 4 КП, включающий правила 1-3s, 2-2s, R-4s и 3-1s, обладают достаточной мощностью детекции предельных изменений величины систематического смещения. Для них в соответствии с международными требованиями выполняются условия: P_fr≤5% и ∆SЕ_min≤∆SЕ_crit. Можно использовать любое их этих правил для надежной детекции случаев выхода АС из-под контроля, которая имеет показатель ∆SЕ_crit = 2,79 или близкой к нему. В качестве случаев выхода АС из-под контроля понимаются случаи изменений начальной величины систематического смещения АС свыше установленной нормы.

Расчеты, проведенные Дж. Вестгардом и другими известными специалистами в области статистических методов лабораторной медицины, показали что традиционные наборы КП при изменениях значений показателя ΔSE от 0 до 1,5 имеют низкую эффективность: вероятность отбраковки аналитических серий при таких изменениях начального смещения не превышает 50% даже при количестве КИ в серии N>4. Отдельно следует отметить, что если число КИ в одной аналитической серии будет равно 1, то вероятность отбраковки серий при изменениях ΔSE от 0 до 1,5 не будет превышать 10%. Отсюда вытекает, что при достаточно малых значениях ΔSE_crit не представляется возможным вести оперативный контроль АС наборами из традиционных КП в соответствии с международными требованиями к его качеству даже при увеличении КИ в серии до четырех. Напомним еще раз, что в международных стандартах рекомендуется использовать такие наборы КП и такое количество КИ в аналитической серии, чтобы вероятность ложной отбраковки «хороших» серий P_fr была ниже 5%, а вероятность P_ed отбраковки «плохих» серий при ΔSE = ΔSE_crit была не ниже 90%.

Стоит отметить, что если для выбранного набора КП показатель ΔSE_min<ΔSE_cri, то можно с уверенностью утверждать, что вероятность детекции случаев выхода АС из-под контроля будет больше 90%. Величина показателя ΔSE_min зависит только от набора КП и количества КИ в серии, а величина показателя ΔSE_crit зависит только от измерительных свойств самой AC. Поэтому для любой АС с АХ в пределах установленных требований можно в принципе всегда подобрать соответствующие набор КП и количество КИ в серии, которые будут обеспечивать выполнение требуемых условий: P_fr≤5% и ∆SЕ_min≤∆SЕ_crit.

Как уже упоминалось выше, при достаточно небольшой величине показателя ΔSE_crit практически любые наборы из одиночных КП крайне неэффективны при малых количествах КИ в серии. Из Рис. 9.6 видно, что такие КП при количестве КИ в серии N = 1 могут быть эффективными, только если ΔSE_crit не меньше 3,5. Поэтому нужно либо подбирать специальный набор из нескольких КП, одновременно несколько увеличивая и показатель N, либо значительно увеличивать для одиночных КП количество КИ в серии. В противном случае произошедшие выходы АС из-под контроля могут быть обнаружены с требуемой вероятностью только лишь по прошествии нескольких аналитических серий. Также отметим, что чрезмерно большое количество КИ в серии приводит, в свою очередь, к увеличению вероятности ложной отбраковки P_fr. Поэтому международные руководства рекомендуют при подборе КП для ведения оперативного контроля конкретной АС с минимально возможным количеством КИ в серии помимо наборов из традиционных КП также использовать правила на основе EWMA с различными контрольными границами. Аналогичной мощностью детектирования «поломок» АС с небольшими по величине показателями ΔSE_crit обладает также рассмотренное выше КП на основе критерия Колмогорова. Расчеты показывают, что КП по Колмогорову при допускаемом значении P_fr и не очень большом количестве КИ в серии  обеспечивает нужную эффективность детекции предельных изменений смещения у АС с низкими значениями показателя ΔSE_min, которую многие другие наборы КП могут обеспечивать только при величине P_fr порядка 8-9%. Это связано с тем, что по мере увеличения количества КИ в серии вероятность P_fr дляКП по Колмогорову будет стремиться к 5% снизу, а показатель ΔSE_min будет стремиться к нулю. Т.е., если большого количества КИ в серии не избежать, то КП по Колмогорову будет предпочтительнее, чем использование любого из традиционных наборов КП.

Как упоминалось выше, руководство [10] по ведению оперативного контроля качества результатов количественных тестов, разработанное CLSI в 2006 году, и проект руководства по ведению ВКК аналитических результатов в медицинской лаборатории [3], разработанный в 1996 году европейской рабочей группой экспертов по лабораторной медицине, рекомендуют использовать именно вероятности P_fr и P_ed в качестве основных критериев правильности выбора соответствующих набора КП и количества КИ в серии. Для ведения оперативного контроля АС оба руководства рекомендуют использовать такие наборы КП и такое количество КИ в серии, чтобы вероятность P_fr ложной отбраковки на самом деле «хорошей» серии была ниже 5%, а вероятность отбраковки P_ed действительно «плохой» серии была бы не меньше 90% при ΔSE = ΔSE_crit. Таким образом оба руководства рекомендуют, чтобы лаборатория, подбирая для ведения оперативного контроля АС набор КП и количество КИ в серии, была уверена, что их сочетание будет адекватно ее аналитическим характеристикам. Т.е., что они будут обеспечивать при ведении оперативного контроля АС поддержание вероятности P_fr на уровне не более 5%, а вероятности детекции P_ed на уровне не менее 90%.

Следует отметить, что правила [11] и другие руководства [12, 13] по проведению процедур ВКК, используемые в настоящее время отечественными лабораториями, в принципе не предусматривают использование критериев качества для ведения процедур оперативного контроля АС, например в виде вероятностей P_fr и P_ed. В этих документах также не предусматриваются принципы адекватного выбора наборов КП и количеств КИ в аналитической серии. Во всех этих документах для ведения оперативного контроля любой АС рекомендуется один и тот же набор КП в виде 7 мультиправил Вестгарда. Количество КИ в серии тоже жестко регламентируется: для ведения оперативного контроля АС лаборатория должна использовать два аттестованных контрольных материала в двух диапазонах определяемых показателей, проводя в каждой аналитической серии однократное измерение показателя в контрольных материалах и образцах пациентов, причем число измерений в аналитической серии не ограничивается. Стабильность АХ АС оценивается по результатам исследования контрольных материалов в каждой аналитической серии, для чего полученные в серии КР проверяются последовательно по каждому из 7 мультиправил. Так как некоторые КП из этого набора, такие как правила 4-1s и 10Хср, требуют для проверки стабильности АХ АС больше, чем 2 КР, то даже при условии их эффективности, о которой в действующих руководствах никакой информации нет, сигнал о выходе АС из под контроля, произошедшем в процессе проведения текущей серии, можно получить только с задержкой в несколько серий. То есть не в режиме реального времени, как хотелось бы. Например, проверка стабильности АХ АС на основе правила 10Хср требует наличия 10 КР подряд. Допустим, что в каждой серии проводится по одному КИ. Тогда, если в процессе проведения какой-либо серии произойдет выход АХ АС за пределы установленной нормы, что в конце концов приведет к нарушению правила 10Хср, то лаборатория узнает об этом только через 9 серий после случившейся «поломки». Как показывает опыт, при ведении оперативного контроля АС, у которых ΔSE_crit<2,5, обнаружить «поломку» непосредственно после проведения серии крайне сложно. Единственное КП, которое может сработать сразу же, – это правило 1-3s. Причем, если у АС показатель ΔSE_crit<2,5, то вероятность срабатывания правила 1-3s при одном КР в серии будет не больше 31%, что нельзя считать эффективным определением «поломок» АС.

Для сравнения эффективности детекции случаев недопустимых изменений систематики АС на Рис 9.8 представлены функции мощности отбраковки «плохих» серий как набором из 7 традиционных мультиправил Вестгарда, так и более современными наборами КП на основе статистик EWMA и Колмогорова. Предполагается, что в каждой серии проводится по одному КИ. Как видно из графиков и таблицы, представленных на этом рисунке, вероятность P_fr для всех рассматриваемых наборов КП не превышает 5%. В то же время вероятность P_ed, которая увеличивается по мере роста величины изменения систематического смещения АС, для набора из 7 традиционных мультиправил Вестгарда достигает значения в 90% только для таких АС, которые имеют показатель ΔSE_crit≥4,5, что соответствует АС с крайне высокими по точности характеристиками. Заметим, что такие аналитические характеристики пока еще практически не достижимы.

Отсутствие в традиционных технологиях ведения оперативного контроля АС механизмов оценки эффективности детекции случаев выхода АС из-под контроля при использовании любого набора КП, в том числе традиционного набора из 7 мультиправил Вестгарда, со временем потребовало их доработки.

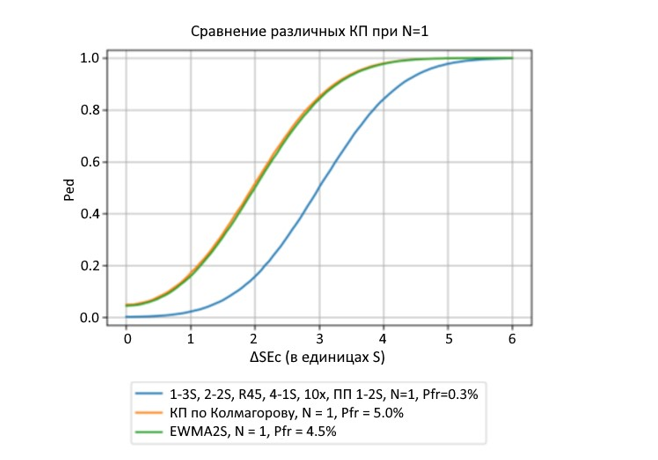
Рис. 9.8. Сравнение функций мощности детекции изменений систематического смещения с использованием наборов традиционных и современных КП на базе статистик EWMA и Колмогорова. Для КП на основе статистики EWMA сглаживающая константа λ = 0,5.

Современные международные руководства по ведению ВКК, например руководства [10, 3, 16], уже содержат новые показатели качества отбраковки аналитических серий в виде вероятностей P_fr и P_ed и механизмы адекватного подбора КП и количества КИ в серии с оптимальным их сочетанием, в зависимости от запаса прочности по точности аналитических характеристик АС, вводимой в эксплуатацию.

Для «персонального» подбора набора КП и количества КИ в серии, учитывающего эксплуатационные значения аналитических характеристик АС, используются графики так называемых функций мощности детекции наборами КП случаев изменения АХ в процессе эксплуатации АС, которые, в свою очередь, зависят от количества КИ в серии. Базовый алгоритм подбора адекватных АС набора КП и количества КИ в серии, рекомендуемый в руководстве [10], был заимствован из известной технологии сигма-метрик, разработанной компанией Моторола, и адаптирован для ведения оперативного контроля АС [15].

Технология сигма-метрик позволяет подбирать для каждой конкретной АС такой набор КП, который будет обеспечивать заданный уровень для вероятности обнаружения случаев запредельных изменений АХ АС при минимально возможном количестве КИ в серии. Цель, которая преследуется в технологии сигма-метрик, состоит в подборе для конкретной АС такого набора КП и такого количества КИ в серии, чтобы они обеспечивали не менее, чем 90% вероятность отбраковки P_ed фактически «плохих» аналитических серий при условии, что вероятность их ложной отбраковки P_fr не будет превышать 5%. В любом случае следует иметь ввиду, что если значения АХ АС, установленные по результатам проведения установочной серии, окажутся близкими к своим предельно допустимым значениям, то невозможно обеспечить должный уровень контроля качества результатов без значительного увеличения количества КИ в аналитической серии.

В технологии сигма-метрик обычно используют следующие параметры:

• B_ac и S_ас – систематическое смещение и стандартная ошибка (среднеквадратичное отклонение) искомой АС, определенные по результатам установочной серии;
• N – количество КИ в одной аналитической серии;
• ∆SE – безразмерный показатель меры изменения систематического смещения, который показывает на сколько значений стандартной ошибки S_ас изменилось начальное значение систематического смещения В_ас АС в процессе ее эксплуатации; текущие значения показателя ∆SE рассчитываются по формуле (9.2);
• ΔSE_crit – безразмерный показатель запаса по правильности, который характеризует критическое изменение систематического смещения и представляет собой максимально допустимое изменение в единицах S_ac начального систематического смещения В_ас; значения показателя ΔSE_crit рассчитываются по формуле (9.6);
• ΔSE_min – минимальное значение показателя ∆SE, при котором вероятность отбраковки серии конкретным набором КП будет равна 90%;
• P_fr – вероятность ложной отбраковки на самом деле «хороших» аналитических серий;
• P_ed – вероятность отбраковки серии на самом деле «плохих» аналитических серий.

Сразу отметим, что для практической реализации механизма технологии сигма-метрик требуются данные о функциях мощности различных наборов КП, то есть о вероятностях отбраковки аналитических серий в зависимости от изменения той или иной аналитической характеристики АС в процессе ее эксплуатации. Например, от изменения систематического смещения АС, которое в технологии сигма-метрик характеризуется показателем ∆SE, измеряемым в единицах стандартной ошибки S_ac. Графики функций мощности для достаточно большого количества различных наборов КП представлены, например, в руководстве [10] и в статье Дж. Вестгарда [1].

Последовательность шагов, которые необходимо предпринять для реализации адекватного выбора КП и количества КИ в серии для ведения оперативного контроля АС с должным качеством, изложена в руководстве [10] и состоит в следующем:

— выбирают конкретные значения для вероятностей P_fr и P_ed, как основных показателей качества процедуры отбраковки серий при ведении оперативного контроля АС, полагая, что значение для P_fr не должно быть более 5%, а значение для P_ed должно быть не менее 90% при существенных изменениях АХ;

— определяют предельно допускаемое абсолютное или относительное значение для полной ошибки TE_a для исследуемого аналита, используя, например, данные, приведенные в таблице на сайте Дж. Вестгарда [2];

— оценивают начальные эксплуатационные значения для систематического смещения В_ас и стандартной ошибки S_ac по данным установочной серии;

— определяют для исследуемого аналита значение его уровня, наиболее важного для принятия клинических решений;

— на основе клинически важного значения уровня аналита и абсолютных значений для ТЕ_а, В_ас и S_ac рассчитывают их относительные значения в процентах;

— определяются с типом и видом КП (традиционные, на основе статистики EWMA или других статистик), которые предполагается использовать в качестве кандидатов для ведения оперативного контроля конкретной АС;

— оценивают предполагаемую эффективность отбраковки серий в процессе эксплуатации АС в терминах вероятности отбраковки серий, включая вероятность ложной отбраковки «хороших» серий, используя для этого имеющиеся в литературе или рассчитанные самостоятельно графики функций мощности детекции существенных изменений АХ наборами КП, выбранными в качестве кандидатов для ведения оперативного контроля АС;

— устанавливают требования к качеству детекции случаев запредельных изменений АХ АС, полагая вероятность отбраковки «плохих» серий, равной 90% или более, а вероятность ложной отбраковки «хороших» серий, равной 5% или менее процентов;

— и, наконец, выбирают конкретный набор КП и конкретное количество КИ в серии, которые будут обеспечивать с заданной вероятностью детекцию случаев критического изменения рассматриваемой АХ АС, используя графики функций мощности для выбранных в качестве кандидатов наборов КП при различных количествах КИ в серии.

Последний шаг в этой технологии предусматривает вычисление критической величины изменения для АХ, обычно для систематического смещения ΔSE_crit. Именно такое изменение начального систематического смещения должно детектироваться с вероятностью не менее 90%. Значения этого показателя, как упоминалось выше, рассчитывают по формуле (9.6), а именно:

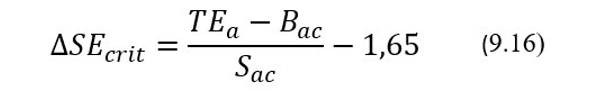
где начальные значения для B_ac и S_ac, а также предельно допускаемое значение для полной ошибки TЕ_a, обычно берутся в процентах, т.е. вместо, например, стандартной ошибки S_ac используется коэффициент вариации CV_ас.

Выражение [(TE_a,%–B_ac,%)/CV_ac)] получило название Sigma-metric. Собственно, отсюда и происходит название технологии сигма-метрик. Показатели ∆SЕ_crit и Sigma-metric связаны между собой следующим образом:

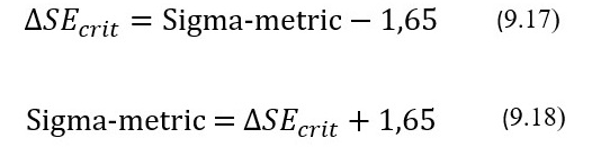
В результате алгоритм выбора процедуры для оперативного контроля АС, рекомендуемый в руководстве [10], включает вкратце следующую последовательность действий:

а) вычисление по результатам установочной серии начальных эксплуатационных значений В_ас и S_ac соответственно для систематического смещения и стандартной ошибки АС;

б) уточнение наименования аналита, исследуемого на АС, с целью определения максимально допускаемого значения ТЕ_а для полной ошибки ТЕ_а = В_а+1,65*S_a, где В_а и S_a – предельно допускаемые значения смещения и стандартной ошибки АС для измерений уровней искомого аналита в пробах пациентов;

б) установление уровня аналита, важного для принятия клинических решений;

в) вычисление c использованием клинически важного уровня аналита относительных значений в процентах для показателей ТЕ_а, В_ас и S_ac, т.е. значенийдля ТЕ_а,%, В_ас,% и CV_ac;

г) вычисление значения для показателя Sigma-metric = (TE_a,%–B_ac,%)/СV_ac;

д) вычисление значения для показателя ∆SE_crit = [(TE_a,%–B_ac,%)/СV_ac]–1,65;

е) установление значений вероятностей P_fr и P_ed, как основных показателей качества отбраковки серий;

ж) определение с помощью графиков функций мощности и установленных значений для вероятностей P_fr и P_ed соответствующей комбинации из набора КП и количества КИ в серии.

Практическое применение алгоритма выбора набора КП и количества КИ в серии для процедуры ведения адекватного оперативного контроля продемонстрируем с помощью примера, приведенного в руководстве [10] для набора из традиционных КП. В качестве аналита в примере используется холестерин, для которого в соответствии с [2] относительное предельно допустимое значение для полной ошибки ТЕ_а = 9%. Предполагается также, что для уровня принятия клинических решений, соответствующего концентрации 200 мг/дл, для смещения и коэффициента вариации АС по данным установочной серии были получены значения В_ас,% = 1,0% и CV_ас = 2,0%. Таким образом показатель ∆SЕ_crit для рассматриваемой АС составит величину: ∆SЕ_crit = {[TЕ_a,% – B_ac,%]/CV_ac)}–1,65 = 2,35.

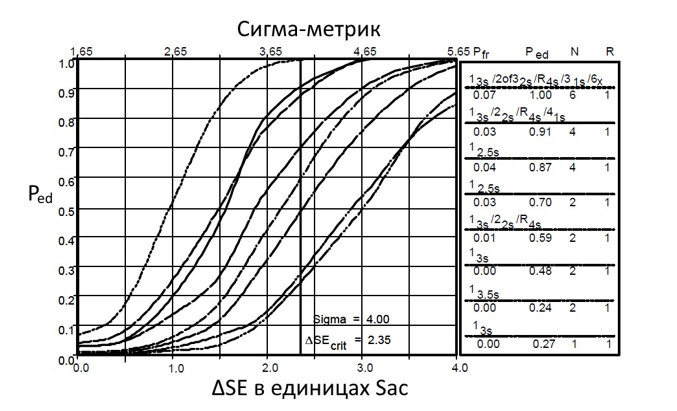
Рис. 9.9. Функции мощности детекции изменений систематического смещения типовой АС для измерения уровней холестерина традиционными КП. Показатель ∆SЕ_crit = 2,35, N – количество КИ в серии, R – количество серий.

На Рис. 9.9 показаны графики функций мощности детекции случаев изменения систематического смещения АС, предназначенной для измерения уровней холестерина, с использованием традиционных КП в том же виде, как они представлены в руководстве [10]. Как видно из этого рисунка, первый набор КП оказывается очень эффективным для детекции запредельного изменения смещения, если количество КИ в серии N = 6. Хотя при такой комбинации первого из наборов КП и N = 6 обеспечивается вероятность отбраковки P_ed, равная почти 100%, но в то же время вероятность ложной отбраковки P_fr оказывается вблизи 7%, т.е. существенно выше максимально допускаемого для нее значения в 5%. Оптимальными для ведения оперативного контроля данной АС следует признать вторую и третью комбинации наборов КП и количества КИ в серии N = 4. Обе эти комбинации имеют вероятность P_ed для критического изменения смещения вблизи 90% и вероятность P_fr меньше 5%.

При подборе КП и количества КИ с серии следует иметь ввиду, что увеличение для одного и того же КП количества КИ в серии приводит, с одной стороны, к увеличению вероятности P_ed, как это следует из данных для правила 1-3s, приведенных на Рис. 9.6 и 9.7, но, с другой стороны, как видно из Таблицы 9.2, это приводит и к увеличению вероятности Р_fr. Заметим также, что, как следует из формулы 9.16, при одном и том же начальном значении стандартной ошибки S_ac значения показателей ∆SЕ_crit и Sigma-metric будут увеличиваться по мере уменьшения начального значения систематического смещения В_ас. Иными словами, чем меньше будет начальное значение систематического смещения, тем больше будет величина ∆SЕ_crit и тем эффективнее будет детекция «поломок» АС одним и тем же набором КП с одним и тем же числом КИ в серии, поскольку по мере роста показателя ∆SЕ увеличиваются и значения функций мощности.

Краткие выводы по Лекции 9.

1. В современных технологиях ВКК для оценки качества процедуры ведения оперативного контроля АС используются два показателя: вероятность P_fr ложной отбраковки на самом деле «хороших» аналитических серий и вероятность P_ed отбраковки на самом деле «плохих» аналитических серий.
2. Хорошими считаются аналитические серии, если полная ошибка ТЕ_ас, полученных в них результатов, не превышает своего предельно допустимого значения TЕ_a или если результаты были получены в условиях, когда начальная прецизионность АС остается стабильной в процессе ее эксплуатации, а величина изменения начального систематического смещения не превышают своего предельно допустимого значения.
3. Предельно допустимое изменение ∆SE_crit начального эксплуатационного значения систематического смещения В_ас определяется в единицах начального значения стандартной ошибки S_ac и вычисляется по формуле ∆SE_crit = [(TE_a–B_ac)/S_ac)]–1,65.
4. Приемлемыми для ведения оперативного контроля АС считаются такие процедуры, при выполнении которых вероятность ложной отбраковки хороших серий P_fr не превышает 5% в условиях стабильности аналитических характеристик АС, а вероятность отбраковки плохих серий P_ed равна или превышает 90% при изменении систематического смещения, равного или свыше ∆SE_crit.
5. Основными параметрами процедуры оперативного контроля АС, обуславливающими ее качество, являются набор КП и количество КИ в аналитической серии.
6. Соответствующую комбинацию, состоящую из набора КП и количества КИ в серии, которая способна обеспечить требуемое качество процедуры оперативного контроля исследуемой АС, подбирают по результатам анализа эффективности детекции изменений аналитических характеристик АС различными комбинациями этих параметров, предлагаемыми в качестве кандидатов. С этой целью для каждой комбинации строят так называемый график функции мощности, представляющий собой вероятность отбраковки серий в зависимости от величины изменения аналитической характеристики, обычно от величины изменения систематического смещения АС. Для ведения оперативного контроля АС выбирают такую комбинацию набора КП и количества контрольных измерений в серии, которая обеспечивает вероятность отбраковки плохих серий P_ed не менее 90% и вероятность ложной отбраковки хороших серий P_fr менее 5%.

Литература к Лекции 9.

1. J.Westgard, T.Groth. Power Functions for Statistical Control Rules. Clinical Chemistry, Vol.25, №6, 1979, p.p. 863-869.
2. https://www.westgard.com/biodatabase1.htm
3. P.Petersen, C.Ricos, D.Stoeckl, J.Libeer, H.Baadenhuijsen, C.Fraser, L.Thienpont. Proposed Guidelines for Internal Quality Control of Analytical Results in the Medical Laboratory. Eur J Clin Chem Biochem, Vol.34, 1996, p.p. 983-999.
4. Kristian Linnet. The Exponentially Weighted Moving Average (EWMA) Rule Compared With Traditionally Used Quality Control Rules. Clinical Chemistry and Laboratory Medicine, Vol.44, Issue 4, 2006, pp. 396-399.
5. S.W.Roberts. Control Chart Tests Based on Geometric Moving Averages. Technometrics, Vol.1, №3, 1959, pp. 239-250.
6. J.S.Hunter. «Exponentially weighted moving average». Journal of Quality Technology, Vol.18, Issue 4, 1986.
7. J.M.Lucas, M.S.Saccucci «Exponentially weighted moving average control schemes: Properties and enhancements», Technometrics, Vol.32, №1, 1990, pp. 1-29.
8. EWMA Control Charts. NIST/Sematech Engineering Statistics Handbook. National Institute of Standards and Technology, https://doi.org/10.18434/M32189
9. Большев Л.Н, Смирнов Н.В. Таблицы математической статистики. Издание третье. Главная редакция физ-мат литературы, М: Наука, 1983. Стр. 347.
10. Clinical and Laboratory Standard Institute Guideline C24-A3. Statistical Quality Control for Quantitative Measurement Procedures: Principles and Definitions; Approved Guideline – 3d Edition, June 2006.
11. Приказ МЗ РФ от 07.02.2000 №45 «О системе мер по повышению качества клинических лабораторных исследований в учреждениях здравоохранения РФ».
12. Приказ МЗ РФ от 26.05.2003 №220 «Об утверждении отраслевого стандарта «Правила проведения внутрилабораторного контроля качества количественных методов клинических лабораторных исследований с использованием контрольных материалов». Приложение. «ОСТ 91500.13.0001-2003».
13. ГОСТ Р 53133.2-2008. Национальный стандарт РФ. «Технологии лабораторные клинические. Контроль качества клинических лабораторных исследований. Часть 2. Правила проведения ВКК качества количественных методов клинических лабораторных исследований с использованием КМ».
14. https://www.westgard.com/six-sigma-calculators.htm
15. Westgard J.O. Six Sigma Quality Design and Control: Desirable Precision and Requisite QC for Laboratory Measurement Processes. Madison, WI: Westgard QC, Inc., 2001.
16.  Jean-Marc Giannoli, Stephanie Albarede, Thierry Avellan, Jean-Pierre Bouilloux, Regine Cartier, Richard Cohen, Nathalie Colard, Luc Essemilaire, Jean-Louis Galinier, Mathieu Kuentz, Mickael Paris, Henri Portugal, Florian Scherrer, Jean-Pascal Siest, Anne Vassault, Jean-Michel Vialle. Recommendations for the application and follow-up of quality controls in medical laboratories (in France). Biochem Med (Zagreb) 2021; 31(2).
17. J.O.Westgard. Internal quality control: planning and implementation strategies. Annals of Clinical Biochemistry, 2003; 40: pp. 593–611.

---

Скачать Лекцию 9