М.И.Прищепа, кандидат технических наук, ЗАО «АНАЛИТИКА»
Настоящая лекция будет посвящена вопросам традиционных технологий мониторинга стабильности аналитических характеристик аналитических систем в процессе их эксплуатации. Наряду с общим описанием алгоритмов детекции случаев изменения аналитических характеристик особое внимание в лекции будет уделено ее теоретическим основам.
Работы по мониторингу стабильности аналитических характеристик в лабораторной медицине принято называть либо оперативным, либо статистическим контролем качества. Вне зависимости от названия важность этого контроля для обеспечения качества лабораторных результатов трудно переоценить. Прежде всего потому, что стабильность аналитических характеристик в процессе эксплуатации аналитических систем (далее – АС) не столь продолжительна как хотелось бы. У многих АС эксплуатационные значения аналитических характеристик (далее – АХ) сохраняются в стабильном состоянии в течение одной или нескольких недель, и даже дольше. Но есть и такие, у которые они сохраняются в течение только одного или нескольких дней. Кроме того, и для тех, и для других АС характерно, что ни момент, ни величина изменений их АХ заранее не известны. Такая неизвестность, по понятным причинам, требует от лабораторий внедрения мер, направленных на обеспечение регулярного контроля стабильности АХ эксплуатируемых АС. Ибо любые изменения АХ, происходящие в процессе эксплуатации АС, будут, в свою очередь, влиять на текущую точность получаемых результатов. Очевидно, что начинать вести контроль стабильности АХ надо сразу же после запуска АС в эксплуатацию, то есть начиная с первого же их определения.
Напомним причины определения изначальных значений АХ АС, а также вкратце опишем последовательность процедур определения этих значений и критерий оценки их приемлемости. Главная причина определения заключается в том, что значения АХ, ввиду их зависимости от конкретных условий эксплуатации АС, заранее не могут быть известны. Отсутствие же такой информации не позволяет лаборатории принять решение о запуске АС в эксплуатацию. Очевидно, что для того, чтобы лаборатория смогла принять такое решение, она прежде должна определить значения АХ для конкретных условий предполагаемой эксплуатации АС, после чего убедиться, что полученные значения соответствуют установленным для них нормам, то есть что они не превышают свои предельно допускаемые значения. Именно поэтому АС устанавливают на ее будущее рабочее место, после чего проводят на ней так называемую установочную серию, состоящую обычно из 20 аналитических серий. В документах [1] и [2] эти 20 серий рекомендуется проводить по одной в день, но в случае крайней необходимости, например, из-за ограниченного срока годности реагентов, допускается проводить и по 2-3 серии в день. В качестве проб в этих сериях используются образцы одного и того же аттестованного контрольного биоматериала, в которых определяют содержание искомого аналита. Затем, на основе полученных результатов, которые принято называть контрольными, проводят оценку значения для математического ожидания, вычисляя их среднее, и оценку значения для дисперсии, вычисляя их стандартное отклонение. Значение для систематического смещения АС определяют как разницу между полученным значением для математического ожидания и аттестованным значением, указанным в паспорте контрольного биоматериала. Если окажется, что определенные таким образом систематическое смещение и стандартное отклонение соответствуют установленным для них нормам, то принимается решение о запуске АС в эксплуатацию и о начале ведения для нее оперативного контроля. Если же полученные значения АХ будут превышать установленные для нормы, то такую АС вводить в эксплуатацию обычно запрещается. При ведении оперативного контроля рекомендуется использовать тот же самый контрольный биоматериал, что и в установочной серии. Следует отметить, что обычно для определения изначальных значений АХ рекомендуется [1, 2] использовать минимум два аттестованных биоматериала – соответственно с патологическим и с нормальным содержанием аналита – и определять значения АХ отдельно для каждого из них. Это связано с тем, что в пределах диапазона измерений АС значения ее АХ зачастую зависят от величины измеряемого уровня аналита. Поэтому и определять изначальные значения АХ и вести оперативный контроль их стабильности рекомендуется [1, 2] как в области нормальных, так и в области патологических уровней аналита.
Переходя далее к вопросам мониторинга стабильности АХ, отдельно отметим, что в основе технологий детекции случаев изменения АХ лежит известный в математической статистике принцип, который принято называть принципом практической невозможности маловероятных событий [3]. Его происхождение связано с опытом решения практических задач, на исходы повторных реализаций которых влияют случайным образом многочисленные слабо действующие факторы. Такая ситуация особенно характерна для сложных систем. Вследствие такого влияния исходы повторных реализаций одной и той же задачи обычно представляют собой некое распределение случайных событий. Для одних исходов характерна высокая вероятность их появления, для других – как средняя, так и низкая. Среди них есть и исходы, вероятность наступления которых в повторных реализациях настолько мала, что ее практически можно считать равной нулю. Теоретически исключить появление в текущей повторной реализации того или иного случайного события, какой бы маленькой вероятностью оно не обладало, конечно, нельзя. Но опыт показывает, что если случайное событие имеет достаточно малую вероятность, то можно полагать, что в результате текущей реализации такое событие не наступит. А если в результате проведения очередной повторной реализации практической задачи такое маловероятное событие все таки происходит, то его появление обычно связывают с произошедшими накануне изменениями параметров задачи или условий ее реализации. Именно этот факт и послужил основой для широкого использования принципа практической невозможности маловероятных событий во многих технологиях контроля стабильности параметров сложных систем, в том числе и в технологиях оперативного контроля стабильности эксплуатационных значений АХ.
Вполне естественно возникает вопрос: а насколько малой должна быть вероятность события, чтобы можно было считать практически невозможным его появление в текущей реализации одного и того же процесса? Этот вопрос в общем случае не имеет однозначного ответа, поскольку он зависит от существа и специфики решаемых задач. Для одних задач такая вероятность должна быть не свыше 1%, для других – она должна быть не свыше 0,1%, для третьих – не свыше 0,01% и т.д. Ближе к концу лекции будет дана количественная оценка вероятности соответствующих маловероятных событий, наступление которых можно считать практически невозможным для решения задач оперативного контроля. Пока же отметим, что значение вероятности, при которой в конкретной задаче появление маловероятного события можно уже считать практически невозможным, в математической статистике принято называть уровнем значимости теста или просто уровнем значимости. Исходя из этого определения уровень значимости можно также интерпретировать как предельно допустимую для данной конкретной задачи вероятность ошибки в сделанном предположении о невозможности наступления случайного события.
В технологиях оперативного контроля в качестве маловероятных случайных событий используют разнообразные комбинации контрольных результатов (далее – КР), вероятности появления которых считаются для этих задач пренебрежительно малыми, если эти КР были получены на АС при неизменных значениях ее АХ. Конкретную комбинацию КР подбирают таким образом, чтобы в условиях стабильности АХ вероятность ее появления в отдельной аналитической серии и/или в относительно небольшом их количестве была настолько малой, чтобы его можно было бы считать практически невозможным. Далее мы выясним какие вероятности для решения задач оперативного контроля можно считать достаточно малыми, и какое количество аналитических серий можно считать относительно небольшим. Комбинации КР с достаточно малыми вероятностями их появления в отдельной или в небольшом количестве аналитических серий принято называть контрольными правилами. И если какая-либо из таких комбинаций КР все-таки появляется по итогам проведения очередной серии, что является практически невозможным событием при неизменных значениях АХ, то тогда говорят, что соответствующее контрольное правило сработало, и делают вывод, что АС вышла из-под контроля. Имея под этим ввиду изменение значений ее АХ, произошедшее в процессе проведения текущей или предыдущих аналитических серий.
Вскользь отметим, что в качестве стабильных по составу контрольных биоматериалов в настоящее время используют главным образом контрольные материалы промышленного изготовления, как для проведении установочных серий, так и для ведения оперативного контроля качества. Это связано с тем, что для обоих предназначений длительная стабильность состава образцов контрольных материалов (далее – КМ) является одним из самых важных их качеств. Сюда же нужно добавить требование низкой вариабельности содержания аналита во флаконах КМ одного и того же лота. Оба эти свойства КМ являются, пожалуй, даже более важными, чем требование их адекватности пробам пациентов.
Полагая, что это очень важно для понимания границ применимости принципа практической невозможности маловероятных событий для задач оперативного контроля, рассмотрим более детально технологию выявления случаев сбоя в работе АС в процессе ее эксплуатации. Итак предположим, что эксплуатационные значения АХ остаются неизменными в процессе эксплуатации АС до какого-то момента времени. Тогда до этого момента все полученные КР, то есть результаты измерений содержания аналита в одном и том же стабильном по составу контрольном биоматериале, будут являться случайными событиями, распределенными по нормальному закону со своим конкретным математическим ожиданием и дисперсией. Такая картина распределения КР обуславливается сложностью воспроизведения измерительных процедур, реализованных в лабораторных АС. Упомянутые основные параметры этого нормального распределения будут, в свою очередь, целиком определяться эксплуатационными значениями АХ. Полученные КР, в соответствии со свойствами нормального распределения, будут концентрироваться вблизи своего математического ожидания, отклоняясь от него главным образом на расстояния не свыше трех сигм, то есть трех стандартных отклонений. Причем, чем сильнее КР отклоняются от математического ожидания, тем меньше вероятность их появления. Зная вероятности появления тех или иных КР можно подбирать из них такие комбинации, которые можно будет рассматривать как достаточно маловероятные события с точки зрения нормального распределения. Из них можно выбрать настолько «маловероятные» события, появление которых в относительно небольшом количестве проводимых серий можно считать практически невозможным при соответствующем уровне значимости. Правда только до тех пор, как будет показано далее, пока общее количество проведенных серий не начнет уже влиять на вероятность появления этих «маловероятных» событий в последующих сериях. Так, например, если вероятность появления какого-либо КР в единичной серии равна 0,1%, то есть одной тысячной, то ее в некотором смысле можно считать близкой к нулю. Но это также означает, что такой КР все-таки может с достаточно большой вероятностью появляться в среднем один раз на тысячу серий. Соответственно, если общее количество серий будет приближаться к тысяче, то тогда вероятность появления этого «маловероятного» события будет приближаться к единице. Таким образом, если количество маловероятных КР в серии и общее количество проведенных серий относительно невелики, что сохраняет вероятность появления таких КР в каждой из них на прежнем низком уровне, то тогда появление этих КР можно считать практически невозможными событиями для АС, имеющей стабильные значения АХ. А их появление в какой-либо очередной серии будет скорее всего говорить о произошедшем накануне изменении ее АХ. Собственно говоря, именно такой алгоритм и используется в технологии детекции случаев изменения АХ в процессе эксплуатации АС.
Как уже упоминалось выше, в качестве средств детекции случаев изменения значений АХ в процессе эксплуатации АС в технологиях оперативного контроля применяют контрольные правила в виде маловероятных комбинаций КР, настолько маловероятных, что их появление в очередных сериях считается практически невозможными событиями. Все это справедливо только для условий, когда значения АХ остаются в процессе эксплуатации АС неизменными. Соответственно, если какие-либо маловероятные комбинации КР все-таки появляются в очередной серии, то полагают, что это скорее всего обусловлено произошедшим накануне изменением АХ. В таких случаях обычно говорят, что сработало соответствующее контрольное правило, сигнализируя о нарушении стабильности АХ.
Такие маловероятные комбинации КР по сути являются сенсорами или детекторами происходящих изменений АХ. Действительно, до момента срабатывания какого-либо сенсора, то есть контрольного правила, изначальные аналитические характеристики АС считаются неизменными. С момента срабатывания любого сенсора, то есть с момента появления соответствующей маловероятной комбинации КР, начинают считать, что в изначальной правильности и/или прецизионности произошли изменения. Таким образом, срабатывание сенсора в виде контрольного правила означает, что АС, как говорят, вышла из-под контроля. При этом начальной серией выхода АС из-под контроля считается та, в которой был получен первый из комбинации КР, соответствующей сработавшему контрольному правилу. В таких случаях рекомендуется [1, 2] отложить и отозвать выдачи заказчикам всех результатов по пациентам, полученных в серии или сериях с использованием АС, вышедшей из-под контроля, вплоть до выяснения причин, приведших к срабатыванию такого сенсора.
Важно отметить, что сами по себе такие технологии ведения оперативного контроля с использованием КМ не являются идеальными. Это связано с тем, что срабатывание контрольных правил теоретически возможно и для АС со стабильными АХ. В результате чего, могут реализовываться случаи ложной отбраковки результатов одной или даже нескольких хороших аналитических серий. В случае использования типовых контрольных правил, которые будут описаны ниже, вероятность ложных отбраковок будет составлять около 0,3%, что в лабораторной медицине считается вполне разумным и допустимым. С другой стороны, контрольные правила допускают случаи пропуска аналитических серий, проведенных на АС, у которых АХ накануне уже изменились. Это, в свою очередь, связано с тем, что комбинации КР, используемые в контрольных правилах, появляются далеко не в 100% случаев изменения АХ. Как будет показано в следующей лекции, вероятность детекции случаев изменения АХ определяется числом контрольных измерений в единичной аналитической серии и выбираемым набором контрольных правил. Вообще говоря, в технологиях контроля, базирующихся на статистических принципах, ничего абсолютного не бывает и быть не может. Это следует из того, что и сам процесс измерения, и его результаты являются по своей сущности случайными событиями. Именно поэтому и сами технологии оперативного контроля тоже описывается языком теории вероятности и математической статистики. И все делаемые в них заключения носят вероятностный характер.
Теперь начнем шаг за шагом двигаться к установлению уровня значимости, то есть определению того, насколько малой должна быть вероятность случайных событий в виде комбинаций КР, чтобы их появление можно было бы считать практически невозможным при решении задач оперативного контроля. С этой целью проведем оценку вероятностей появления комбинаций КР, на основе которых формируются типовые контрольные правила, в условиях стабильности АХ. Наиболее часто используемые на практике типовые контрольные правила описываются ниже. Их всего пять. Они обычно обозначаются как 1-3s, 2-2s, R-4s, 4-1s и 10Xср.
1-3s. Первое из упомянутых контрольных правил, обозначенное как 1-3s, содержит в своем обозначении описание появления случайного события, маловероятного с точки зрения нормального распределения. Это событие наступает, когда текущий КР выходит либо за пределы Хср+3S, либо за пределы Хср–3S. Если это происходит, то говорят, что контрольное правило 1-3s сработало, и что АС вышла из-под контроля. Здесь Хср – оценка математического ожидания в виде среднего, а S – оценка дисперсии в виде стандартного отклонения, которые изначально вычисляются по результатам установочной серии.
2-2s. Второе контрольное правило, обозначенное как 2-2s, описывает появление случайного события, также маловероятного с точки зрения нормального распределения, которое наступает тогда, когда два последних КР выходят либо за пределы Хср+2S, либо за пределы Хср–2S. Если это происходит, то говорят, что контрольное правило 2-2s сработало.
R-4s. Третье контрольное правило, обозначенное как R-4s, описывает появление случайного события, также маловероятного события с точки зрения нормального распределения, когда два последовательных КР располагаются по разные стороны от коридора Хср+2S и Хср–2S. Если это происходит, то говорят, что контрольное правило R-4s сработало.
4-1s. Четвертое контрольное правило, обозначенное как 4-1s, описывает появление случайного события, также маловероятного с точки зрения нормального распределения, когда четыре последовательных КР выходят либо за пределы Хср+1S, либо за пределы Хср–1S. Если это происходит, то говорят, что контрольное правило 4-1s сработало.
10Хср. И, наконец, пятое контрольное правило, обозначенное как 10Хср, описывает появление события, также маловероятного с точки зрения нормального распределения, когда 10 последовательных КР все оказываются либо больше, либо меньше Хср. Если это происходит, то говорят, что контрольное правило 10Хср сработало.
Следует отметить, что срабатывание контрольного правила 1-3s связано обычно с произошедшим накануне изменением либо систематического смещения, либо стандартного отклонения, либо с изменением обеих этих характеристик одновременно. Срабатывание контрольного правила R-4s бывает обычно обусловлено произошедшим накануне изменением стандартного отклонения, а срабатывание какого-либо из остальных контрольных правил обычно бывает обусловлено произошедшим изменением систематического смещения.
Также отметим, что наряду с описанными выше контрольными правилами, нередко используют и другие как контрольные, так и предупредительные правила. Предупредительные правила срабатывают на появление событий, которые хотя и являются достаточно редкими, но их появление, как будет показано далее, еще нельзя считать практически невозможным для задач оперативного контроля. К предупредительным относят правила типа 1-2s или 1-2,5s, которые срабатывают, когда текущий КР выходит за пределы Хср+2S (Хср+2,5S) или за пределы Хср-2S (Хср–2,5S). Срабатывание таких правил не является основанием полагать, что АС вышла из-под контроля. Но дает знать о том, что это может случиться в ближайшее время.
Для вычисления вероятностей появления комбинаций КР, которые лежат в основе срабатывания наиболее часто используемых контрольных и предупредительных правил, нам понадобятся соответствующие значения интегральной функции Лапласа Ф(z), о которой речь шла в предыдущих лекциях. Эти значения позволят определять вероятности того, что случайная величина попадет в тот или иной интервал ее возможных значений. Значения интегральной функции Лапласа Ф(z) можно вычислить самостоятельно, используя в приложении Microsoft Excel функцию НОРМСТРАСП для старых версий этого приложения или функцию НОРМ.СТ.РАСП для последних его версий [4]. Или, как и в предыдущих лекциях, можно воспользоваться уже готовыми табличными значениями этой функции [5].
Для самостоятельного вычисления значений интегральной функции Лапласа Ф(z), где аргумент z указывается в единицах стандартного отклонения S, надо в приложении Excel выбрать в разделе «Формулы» подраздел «Вставить функцию» и в появившемся окне «Поиск функции» набрать «НОРМСТРАСП» или «НОРМ.СТ.РАСП», после чего нажать с помощью курсора на клавишу «Найти». В перечне функций появится функция «НОРМСТРАСП» или «НОРМ.СТ.РАСП», которую надо выделить с помощью курсора и затем нажать на клавишу «ОК». На появившейся странице «Аргументы функции» надо в cтрочке Z вставить искомое значение аргумента z функции Ф(z) в единицах стандартного отклонения S. Например, чтобы вычислить значение функции Ф(z) для случайной величины x=Хср+2S, то есть отстоящей от Хср на 2 стандартных отклонения S, надо в строчке для Z поставить цифру 2. В строчке «Интегральная» надо поставить цифру 1. В верхней строчке основной страницы Excel отобразиться надпись искомой функции Ф(х) «=НОРМСТРАСП(2,1) или «=НОРМ.СТ.РАСП(2,1). Надо в эту строку дописать «–0.5», то есть вычесть 0.5 из функции Ф(2,1). В результате получим величину 0,47725, что и есть искомое значение функции Ф(2). Соответственно, если повторить вышеописанные процедуры для вычисления значения функции Ф(0), то есть при х=0, то тогда получим, что значение Ф(0) будет равно 0.
Как было сказано выше, значения интегральной функции Лапласа Ф(z) позволяют определять вероятность того, что случайная величина, имеющая нормальное распределение, примет значение, принадлежащее заданному интервалу. Ранее в Лекции 7 упоминалось, что для вычисления вероятности P(x1 < x < x2) попадания в интервал (х1; х2) случайной величины х, распределенной по нормальному закону, можно использовать нижеследующую формулу:
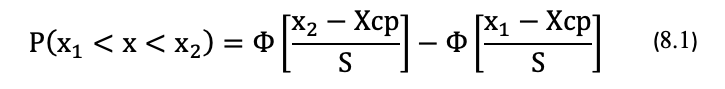
где Ф[(x – Хср)/S] — интегральная функция Лапласа, для которой аргумент z, соответствующий случайной величине х, вычисляется по формуле z = (x – Хср)/S. Откуда следует, что z2 = (x2 – Хср)/S, а z1 = (x1 – Хср)/S.
Как видно из формулы (8.1), вычисление вероятности попадания случайной величины х в искомый интервал с границами х1 и х2 проводится достаточно просто, если нам известны значения функции Ф(z), соответствующие этим границам. Как было сказано выше, нужные значения функции Ф(z) можно выбирать из таблиц [5] или вычислять самостоятельно, пользуясь приложением Microsoft Excel [4].
Выше был представлен пример вычисления значений функции Ф(z) при z=2 и при z=0. Воспользуемся формулой (8.1) и найденными значениями для Ф(z) и определим вероятность того, что ожидаемое значение случайной величины x, распределенной по нормальному закону, попадет в интервал [Хср; Хср+2S]. В итоге получим, что
Р(Хср < x < Хср+2S) = Ф[(Хср+2S – Хср)/S] – Ф[(Хср – Хср)/S] = Ф(2) – Ф(0) = 0,47725 – 0 = 0,47725.
Известно, что интегральная функция Лапласа является нечетной, то есть для нее выполняется равенство: Ф(–z) = –Ф(z). Воспользуемся этим свойством и тогда получим, что Ф(–2) = –Ф(2) = –0,47725. Тогда, соответственно, вероятность того, что текущий результат повторного измерения уровня аналита попадет в интервал [Хср–2S; Хср+2S], будет равна:
Р(Хср–2S < x < Хср+2S) = Ф(2) – Ф(–2) = 0,47725 – (–0,47725) = 0,47725 + 0,47725 = 0,9545.
Теперь, наконец, перейдем непосредственно к количественной оценке уровней значимости, используемых при ведении традиционного оперативного контроля. То есть вычислим вероятности появления соответствующих комбинаций КР, которые обусловливают срабатывание типовых контрольных и предупредительных правил в условиях, когда АХ остаются неизменными. Другими словами, определим вероятности ложного срабатывания этих правил, то есть в условиях, когда АС все еще находятся под контролем.
При проведении вычислений искомых вероятностей появления комбинаций КР будем иметь ввиду, что появления КР являются совместными и независимыми событиями. Напомним, что события называются несовместными, если наступление одного из них исключает появление любого другого. В противном случае, события называются совместными. Соответственно, события называются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий. Действительно, появление любого КР никоим образом не исключает появление иных КР, в том числе и его же, а вероятность появления какого либо КР в текущей аналитической серии не зависит от более раннего появления других КР. Из теории вероятностей известно [3], что вероятность Р(АВ) одновременного появления двух совместных независимых событий А и В, или, как говорят, вероятность произведения этих событий, равна произведению вероятностей Р(А) и Р(В) каждого из этих событий. Вероятность Р(АВ) вычисляют по формуле:
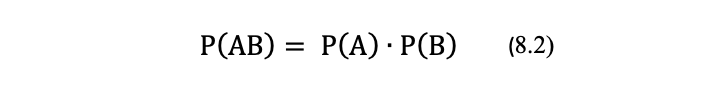
Также отметим, что вероятность произведения трех, четырех и так далее совместных независимых событий будет, как следует из той же теории вероятностей [3], равна произведению вероятностей появления каждого из них. В свою очередь, из теории вероятностей также следует, что вероятность Р(А+В) суммы двух совместных независимых событий равна сумме вероятностей Р(А) и Р(В) каждого из этих событий минус вероятность Р(АВ) их одновременного появления. Вероятность Р(А+В) вычисляют по формуле:
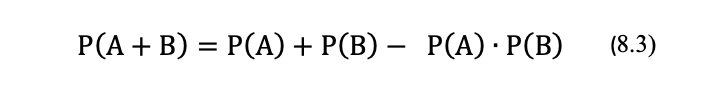
Суммой двух совместных независимых событий называется событие, которое наступает тогда и только тогда, когда наступает хотя бы одно из этих событий. Это означает, что событие А+В наступает тогда и только тогда, когда при наблюдении произошло или событие А, или событие В, или одновременно и событие А, и событие В.
Пользуясь этими определениями и формулами для вычисления вероятностей сумм и произведений совместных независимых событий, сначала покажем, каким образом изменяется вероятность появления какого-либо КР хотя бы в одной аналитической серии по мере увеличения их количества. Будем исходить из того, что вероятность суммы двух совместных независимых событий, то есть вероятность появления хотя бы одного из них, равна сумме вероятностей появления каждого из этих событий за вычетом вероятности их одновременного появления. Отсюда следует, что если в каждой аналитической серии будет проводиться только одно контрольное измерение, то вероятность появления какого либо КР хотя бы в одной из двух аналитических серий будет равна сумме вероятностей появления этого КР в каждой отдельной серии за вычетом их произведения, то есть вероятности его появления в каждой из них. Например, предположим, что вероятность появления какого-либо КР в отдельной аналитической серии равна 0,05 или 5%, что тоже самое, но в процентном выражении. Итак, вероятность появления этого КР в первой серии будет равна 5%. Тогда, используя формулу (8.3), получим, что появление этого КР хотя в одной из первых двух серий будет равна 9,75%=10% – 0,25%, то есть сумме вероятностей его появления в каждой из двух серий минус вероятность его появления в обеих сериях, которая, исходя из формулы (8.2), как раз и будет равна 0,25%=0,05*0,05*100. Таким образом, вероятность появления искомого КР хотя бы в одной из первых двух серий увеличится с 5% до 9,75%. Отметим при этом, что если КР не появился в первой из двух серий, то вероятность его появления во второй серии остается прежней и равной 5%, поскольку эти события являются совместными и независимыми. Теперь вычислим вероятность появления этого же КР хотя бы в одной из трех последовательных серий. Для этого воспользуемся тем, что вероятность его появления в одной двух первых серий равна 9,75%, а в третьей – 5%. Тогда получим, используя формулу (8.3), что вероятность появления искомого КР хотя бы в одной из трех серий будет равна 14,26%=9,75% + 5% – 0,49%, то сумме вероятности его появления хотя бы в одной из первых двух серий и вероятности его появления в третьей серии за вычетом вероятности его появления и в одной из первых двух серий, и в третьей серии, которая, исходя из формулы (8.2), будет равна 0,49%=0,0975*0,05*100. Таким образом, вероятность появления искомого КР хотя бы в одной из первых трех серий увеличится до 14,26%. Еще раз отметим, что если КР не появился ни в одной из первых двух серий, то вероятность его появления в третьей серии остается прежней и равной 5%, поскольку все эти события являются совместными и независимыми. Соответственно, вероятность появления искомого КР хотя бы в одной из четырех серий будет равна 18,55%=14,26% + 5% – 0,71%, то есть сумме вероятности его появления в одной из трех первых серий и вероятности его появления в четвертой серии минус произведение вероятности его появления хотя бы в одной из первых трех серий на вероятность его появления в четвертой серии, которое будет соответственно равно 0,71%=0,1426*0,05*100. Такие вычисления можно продолжить и дальше. Тогда, соответственно, получим, что вероятность появления КР хотя бы в одной из пяти серий будет равна 22,62%, хотя бы в одной из десяти серий будет равна 40,12%, хотя бы в одной из пятнадцати серий будет равна 53,67% и, наконец, хотя бы в одной из двадцати серий будет равна 64,14%.
Еще раз напомним, что из проведенного анализа совершенно не следует, что если искомый КР не появился в результате 20 проведенных серий, то вероятность его появления в следующей 21-ой серии будет больше, чем 5%. На самом деле, поскольку КР являются совместными и независимыми событиями, вероятность появления искомого КР в каждой последующей серии остается постоянной и равной 5%. То же самое справедливо и для заданного количества серий. То есть вероятность появления искомого КР хотя бы в одной из серий остается постоянной: 22,62% при 5 заданных сериях, 40,12% при 10 заданных сериях или 64,14% при 20 заданных сериях. Другое дело, что вероятность появления этого КР хотя бы в одной из 20 серий будет несколько больше, чем вероятность его появления хотя бы в одной из 10, и значительно больше, чем вероятность его появления в одной серии. Также отметим, что вероятность появления искомого КР хотя бы в одной из 20 серий будет равна вероятности суммы двух событий, каждое из которых представляет собой появление искомого КР хотя бы в одной из 10 серий. Действительно, вероятность суммы двух упомянутых событий согласно формуле (8.3) будет равна 0,4012 + 0,4012 – 0,161=0,6414 или 64,14%. Таким образом, из проведенного анализа следует, что хотя вероятности появления какого-либо КР в отдельной аналитической серии или хотя бы в одной из заданного их количества остаются постоянными, но вероятность появления искомого КР хотя бы в одной из искомого количества аналитических серий будет возрастать по мере увеличения этого количества.
Заметим, что аналогичный подход справедлив и для исходов бросания обычного шестигранного кубика с числами от 1 до 6 на его гранях, и для исходов поездок на автомобиле, и полетов на самолете, с точки зрения возможного возникновения неисправностей. Если условия реализации одной и той же задачи (бросания, поездки и полета) остаются неизменными (один и тот же игрок, водитель, пилот, один и тот же игральный кубик, автомобиль, самолет, один и тот же стол, бензин, керосин и т.д., и т.п.), то вероятность искомого исхода остается неизменной для каждой реализации. То есть вероятность выпасть шестерке или вероятность какой-либо поломки автомобиля или самолета остаются неизменными для каждой последующей реализации, поскольку такие события – правда, после ремонта автомобиля и самолета – являются совместными и независимыми. Но вероятность хотя бы один раз из какого-либо заданного количества реализаций выпасть шестерке, сломаться автомобилю или самолету будет увеличиваться по мере увеличения количества реализаций. То есть вероятность выпасть шестерке остается постоянной для каждого последующего бросания вне зависимости от предыдущих исходов, и равной 1/6 или 16,67%. Вероятность же выпасть шестерке хотя бы один раз при заданном количестве проводимых бросаний возрастает по мере их увеличения. Так вероятность выпасть шестерке хотя бы один раз из трех бросаний будет равна 30,56%, а вероятность выпасть хотя бы один раз из шести бросаний будет уже равна 66,51%. Аналогична ситуация и с поездками на автомобиле, и с полетами на самолете. Вероятность поломки для автомобиля или самолета будет оставаться постоянной для каждого последующего выезда или вылета вне зависимости от предыдущих исходов, но вероятность поломки хотя бы в одном из совершенных выездов или вылетов будет возрастать по мере их увеличения.
Теперь, учитывая вышеизложенное, вычислим вероятности появления соответствующих комбинаций КР, которые обусловливают срабатывание типовых контрольных и предупредительных правил в условиях, когда АХ остаются неизменными.
Срабатывание предупредительных правил.
Начнем с правила 1-2s, которое относится к категории предупредительных. Оно описывает появление случайного события, маловероятного с точки зрения нормального распределения, которое происходит, когда текущий КР выходит за пределы Хср+2S или за пределы Хср-2S. Если это происходит, то говорят, что предупредительное правило 1-2s сработало. Итак, подставим в формулу (8.1) соответствующие значения интегральной функции Лапласа [4,5] и определим, как это было уже сделано выше, что вероятность того, что КР в текущей аналитической серии примет значение, принадлежащее интервалу [Хср-2S; Хср+2S], равно 95,45%. Тогда, соответственно, вероятность того, что КР в текущей этой серии выйдет за пределы этого интервала, то есть выйдет или за пределы Хср-2S, или за пределы Хср+2S, составит 4,55%. Таким образом, вероятность того, что в условиях, когда значения АХ остаются неизменными, КР в текущей серии отклонится от Хср свыше 2S, будет равна 4,55%. Это относительно высокая вероятность для маловероятного события, появление которого можно было бы считать практически невозможным. Поэтому правило 1-2s относят не к контрольным, только лишь к предупредительным. Действительно, поскольку, как было показано выше, вероятность появления КР хотя бы в одной из проведенных аналитических серий увеличивается по мере увеличения их количества, то такая величина вероятности означает, что после проведения 20 и более контрольных измерений можно уже с достаточно большой вероятностью ожидать, что хотя бы в одном из них появиться результат, который отклонится от Хср свыше 2S. Другое дело, что он может появиться и в начале, и в середине, и в конце проведения этих серий. Таким образом, если проводить только одно контрольное измерение в день, то тогда можно ожидать, что правило 1-2s с достаточно большой вероятностью будет срабатывать в среднем один раз в месяц даже при неизменных значениях АХ, выдавая ложные сигналы о сбое в работе АС.
Далее таким же образом определим, что вероятность срабатывания правила 1-2,5s в условиях стабильности значений АХ, то есть вероятность появления КР, выходящего либо за пределы Хср–2,5S, либо за пределы Хср+2,5S, составляет около 1,24%. Это почти в 4 раза меньше, чем 4,55%, то есть чем вероятность выхода КР либо за пределы Хср–2S, либо за пределы Хср+2S. Поскольку это тоже относительно высокая вероятность для маловероятного события, появление которого можно было бы считать практически невозможным, то правило 1-2,5s тоже следует отнести к предупредительным. Действительно, такая величина вероятности означает, что в процессе проведения 80 и более контрольных измерений можно уже с большой вероятностью ожидать, что хотя бы в одном из них появиться результат, который отклонится от Хср свыше 2,5S. То есть, если проводить только одно контрольное измерение в день, то тогда правило 1-2,5s будет срабатывать в среднем один раз в 3 месяца даже при неизменных значениях АХ, выдавая ложные сигналы о сбое в работе АС.
Срабатывание контрольных правил.
Далее для тех же условий, когда значения АХ предполагаются стабильными, оценим величины вероятностей ложного срабатывания контрольных правил.
Начнем с контрольного правила 1-3s. Используя формулу (8.1) и табличные значения функции Лапласа находим, что вероятность того, что текущий КР примет значение, принадлежащее интервалу [Хср–3S; Хср+3S], равно 99,73%. Соответственно вероятность выхода текущего КР или за пределы Хср–3S или за пределы Хср+3S составит только 0,27% при неизменных эксплуатационных значениях АХ. По сравнению с вероятностями срабатывания предупредительных правил это уже достаточно малая вероятность, чтобы считать ложное срабатывание контрольного правила 1-3s практически невозможным событием. Действительно, такая величина вероятности означает, что только после проведения 370 и более наблюдений можно с большой вероятностью ожидать появления среди результатов такого, который отклонится от Хср свыше 3S. И если проводить только одно контрольное измерение в течение рабочего дня, то тогда правило 1-3s будет ложно срабатывать в среднем один раз в 12 (если все 7 дней в неделе рабочие) или в 17 месяцев (если только 5 дней рабочие). Напомним, что речь идет о срабатывании правила 1-3s в условиях, когда эксплуатационные значения АХ не изменяются. Поэтому правило 1-3s принято считать уже контрольным, а характеризующее его событие считать практически невозможным. Это является основанием полагать, что появление в аналитической серии КР, отклоняющегося от Хср более, чем на 3S, скорее всего будет обусловлено изменением накануне изначальных эксплуатационных значений АХ. По этой причине все результаты пациентов текущей аналитической серии положено считать сомнительными. И вплоть до выяснения причин срабатывания этого контрольного признака результаты по пациентам, полученные в такой серии, выдавать в клинику запрещается.
Теперь оценим вероятность срабатывания контрольного правила 2-2s в условиях, когда значения АХ АС остаются стабильными. То есть вероятность его ложного срабатывания. Используя формулу (8.1) и, например, табличные значения интегральной функции Лапласа [5] находим, что вероятность того, что при однократном наблюдении КР примет значение, принадлежащее интервалу [Хср–2S; Хср+2S], равно 95,45%. Тогда вероятность того, что текущий КР выйдет за пределы этого интервала, то есть выйдет или за пределы Хср–2S или за пределы Хср+2S составит 4,55%. Соответственно, вероятность того, что второй результат отклонится от Хср тоже более, чем на 2S, но в ту же сторону, что и первый, составит половину от предыдущей и будет равна 2,275%. Тогда, соответственно, вероятность того, что в условиях стабильности АХ два результата подряд отклонятся от Хср более чем на 2S в одну и ту же сторону будет равна чуть более 0,1%. Такая величина вероятности означает, что только после проведения 1000 и более контрольных измерений можно с большой вероятностью ожидать появления среди результатов такой их комбинации, когда 2 КР подряд отклоняются от Хср свыше 2S в одну и ту же от него сторону. Такое событие будет в среднем появляться с частотой один раз в 45 месяцев (если в неделе только 5 рабочих дней), сигнализируя о ложном выходе АС из-под контроля. В этой связи, такое событие следует считать уже практически невозможным для условий, когда значения АХ остаются в процессе эксплуатации АС неизменными. И это является основанием полагать, что срабатывание этого правила обусловлено, скорее всего, изменением изначальных значений АХ. По этой причине все результаты пациентов последней или двух последних аналитических серий следует считать сомнительными. Результаты последней серии не должны выдаваться в клинику, а результаты предыдущей серий, если проводится по одному контрольному измерению в день, должны быть отозваны до тех пор, пока не будут выяснены причины срабатывания этого правила.
Теперь оценим вероятность срабатывания контрольного правила 4-1s в условиях, когда значения АХ остаются стабильными. То есть вероятность его ложного срабатывания. Воспользуемся, как и ранее, формулой (8.1) и соответствующими табличными значениями интегральной функции Лапласа [5], и сначала определим, что вероятность того, что в текущей серии КР примет значение, принадлежащее интервалу [Хср–1S; Хср+1S], будет равна 68,27%. Тогда, соответственно, вероятность выхода текущего КР либо за пределы Хср–1S либо за пределы Хср+1S составит 31,73%. Очевидно, что вероятность того, что каждый из последующих трех КР отклонится тоже либо за пределы Хср–1S, либо за пределы Хср+1S, но в ту же самую сторону, что и первый КР, будет равна только половине от вышеупомянутой вероятности появления первого КР, то есть будет равна 15,87%. Чтобы определить вероятность произведения этих четырех событий, то есть вероятность их совместного появления, необходимо, как упоминалось выше, перемножить вероятности появления каждого из них. Перемножим вероятности появления каждого из этих 4 КР и получим вероятность появления события, когда 4 КР подряд, включая последний, выйдут либо за пределы Хср–1S, либо за пределы Хср+1S. Вероятность этого события будет равна 0,13%. Это достаточно малая вероятность, чтобы считать срабатывание контрольного правила 4-1s практически невозможным событием для условий, когда АХ остаются неизменными. Действительно, такая величина вероятности означает, что только после проведения 770 и более контрольных измерений можно с большой вероятностью ожидать появления среди полученных результатов такой их комбинации, когда 4 КР подряд будут лежать или выше Хср+1S или ниже Хср–1S. Таким образом, в условиях стабильности АХ контрольное правило 4-1s будет в среднем срабатывать один раз в 35 месяцев, сигнализируя о ложном выходе АС из-под контроля. В случае, конечно, если контрольное измерение проводится только один раз в день, а неделя состоит из 5 рабочих дней. Поэтому такое событие считают уже практически невозможным для условий, когда эксплуатационные значения АХ остаются неизменными. И это является основанием полагать, что срабатывание правила обусловлено, скорее всего, изменением их изначальных значений. По этой причине все результаты пациентов текущей и трех предыдущих аналитических серий следует считать сомнительными. Результаты последней серии не должны выдаваться в клинику, а результаты трех предыдущих серий, если проводится по одному контрольному измерению в день, должны быть отозваны до тех пор, пока не будут выяснены причины срабатывания этого правила.
В тоже время следует отметить, что в стабильных условиях АХ вероятность срабатывания правила 3-1s, то есть вероятность того, что 3 последовательных КР выйдут либо за пределы Хср–1S, либо за пределы Хср+1S при неизменных эксплуатационных значениях АХ, составит только 0,82%. Это означает, что только после проведения 122 и более серий при неизменных АХ можно будет с большой вероятностью ожидать ложного срабатывания такого правила, то есть 1 раз в 5-6 месяцев. На этом основании правило 3-1s относят обычно к предупредительным, полагая, что появление последовательности из 3 КР, вышедших за пределы Хср+1S или Хср–1S, можно считать еще допустимым для принятия гипотезы о стабильности эксплуатационных значений АХ.
Теперь оценим вероятность срабатывания контрольного правила R-4s в условиях, когда значения АХ остаются стабильными. Выше было определено, что вероятность того, что в текущей серии КР окажется за пределами интервала [Хср–2S; Хср+2S], то есть выйдет за пределы Хср+2S или за пределы Хср–2S, составляет 4,55%. Вероятность выхода в следующей серии КР за те же пределы, но не в любую, а именно в противоположную от первого КР сторону, будет тогда равна 2,275%. Перемножим вероятности появления каждого из этих двух КР и получим, что вероятность произведения этих событий, то есть вероятность события, когда 2 КР подряд оказываются по разные стороны коридора Хср–2S и Хср+2S, будет равна 0,1%. Такая величина вероятности означает, что только после проведения 1000 и более контрольных измерений можно будет с большой вероятностью ожидать появления среди результатов такой их комбинации. Такое событие, сигнализируя о ложном выходе АС из-под контроля, будет в среднем появляться с частотой один раз в 45 месяцев, если контрольное измерение проводится только один раз в день, а неделя состоит из 5 рабочих дней. Поэтому такое событие считают практически невозможным для условий, когда эксплуатационные значения АХ остаются неизменными. Причина его появления будет, скорее всего, обусловлена изменением их изначальных значений. На этом основании все результаты пациентов последней и предыдущей аналитических серий следует считать сомнительными. Результаты последней серии не должны выдаваться в клинику, а результаты предыдущей серии должны быть отозваны до тех пор, пока не будут выяснены причины срабатывания этого контрольного правила.
И, наконец, оценим вероятность срабатывания контрольного правила 10Хср в условиях, когда значения АХ остаются стабильными. Вероятность появления в аналитической серии первого результата очевидно будет равна 100%. Тогда вероятность появления каждого из остальных 9 КР с той же стороны, что и первый КР, будет 50%. Перемножим вероятности появления каждого из этих десяти КР и получим, что вероятность произведения этих событий, то есть вероятность события, когда 10 КР подряд оказываются с одной и той же стороны от Хср, будет равна 0,195%, то есть чуть менее 0,2%. Эта вероятность даже чуть меньше вероятности ложного срабатывания контрольного правила 1-3s. Такая величина вероятности означает, что только после проведения 500 и более контрольных измерений можно с большой вероятностью ожидать появления среди результатов такой их комбинации, когда 10 КР подряд будут все лежать или выше или ниже от Хср. Это означает, что если проводить только одно контрольное измерение в день, то тогда правило 10Хср будет срабатывать с достаточно большой вероятностью в среднем один раз в 23 месяца при 5 дневной рабочей неделе. Напомним, что речь идет о частоте ложного срабатывания правила 10Хср, то есть для условий, когда эксплуатационные значения АХ не изменяются. Очевидно, что ввиду весьма низкой вероятности срабатывания такого правила в условиях стабильности АХ, появление такой комбинации КР вполне можно относить к практически невозможным событиям, а само правило отнести к контрольным. Причиной срабатывания этого правила будет, скорее всего, являться предшествующее ему изменение изначальных значений АХ. В этой связи, все результаты по пациентам, полученные в течение последних 10 дней или серий, следует считать сомнительными. Соответственно, результаты по пациентам, полученные в последний день, в клинику выдавать не следует, а результаты за предыдущие 9 дней рекомендуется отозвать. Вплоть до выяснения причин срабатывания этого контрольного правила эксплуатацию АС разумно приостановить. Такая «катастрофическая» ситуация может возникать, если проводить в течение рабочего дня только одно контрольное измерение. Очевидно, чтобы получить возможность с помощью правила 10Хср детектировать выходы АС из-под контроля в режиме реального времени, необходимо проводить ежедневно, по крайней мере, 10 контрольных измерений.
Следует отметить, что обычно любой сбой в работе АС приводит к достаточно однообразным изменениям эксплуатационных значений АХ сразу же во всем диапазоне измерений АС, то есть во всем диапазоне измерения содержания аналита, заявленного изготовителем. В таких случаях ежедневные КР, получаемые в течение дня для всех КМ, можно объединять при проведении оценки срабатывания контрольных правил, сигнализирующей о выходе АС из-под контроля. Так, при использовании для оперативного контроля двух КМ с содержанием аналита на уровне нормы и на уровне патологии, количество КР, которые можно использовать для мониторинга стабильности АХ, будет равно уже двум при одном ежедневном контрольном измерении уровня аналита в каждом КМ. И если оба КР, полученные в течение дня для каждого из двух КМ, отклонятся каждый от своего среднего более, чем на 2 своих стандартных отклонения, то тогда можно полагать, что сработало правило 2-2s, если оба КР отклонились в одну и ту же сторону от своих Хср. И, соответственно, что сработало контрольное правило R-4s, если эти КР отклонились по разные стороны от своих Хср. Понятно, что такие 2 КР в день не сильно улучшат «катастрофическое» состояние с результатами по пациентам для контрольного правила 10Хср в случае его срабатывания из-за реального сбоя в работе АС, поскольку это срабатывание произойдет только на пятый рабочий день после поломки. Зато при ежедневном наличии таких двух КР контрольные правила 2-2s и R-4s могут с большой вероятностью срабатывать в течение одного и того же рабочего дня при сбое в работе АС, произошедшем в самом начале рабочего дня. Также достаточно очевидно, что для того, чтобы контрольное правило 4-1s в таких же случаях сбоя в работе АС срабатывало без задержек в течение текущего рабочего дня, необходимо делать ежедневно по два контрольных измерения в каждом из двух КМ. Соответственно, чтобы контрольное правило 10Хср в таких же случаях сбоя в работе АС срабатывало в течение текущего рабочего дня, необходимо делать ежедневно по крайней мере по пять контрольных измерений в каждом из двух КМ.
Далее, чтобы получить представление о динамике изменения вероятности появления маловероятных с точки зрения нормального распределения событий, проведем пошаговый анализ ситуаций, когда меньше, чем 10 КР подряд оказываются выше или ниже Хср. Начнем с ситуации, когда 5 КР подряд оказываются все выше или ниже Хср. Как упоминалось ранее, вероятность появления в текущей серии второго и последующих КР равна 50%. Вероятность появления первого результата равна 100%. Перемножим вероятности появления каждого из пяти КР и получим, что вероятность появления при неизменных значениях АХ пяти КР подряд, располагающихся выше или ниже Хср, будет равна 6,25%. Эта величина вероятности означает, что такое событие будет появляться даже без сбоя в работе АС в среднем через каждые 16 контрольных измерений, то есть через каждые 16 или 8 рабочих дней соответственно при одном или двух ежедневных контрольных измерениях. То есть такое событие в условиях стабильности АХ может появляться относительно часто. Поэтому на однократное появление такого события вряд ли стоит обращать особое внимание, хотя по частоте повторения оно достаточно близко к предупредительному правилу 1-2s. Напомним, что вероятность ложного срабатывания правила 1-2s, то есть в условиях стабильности АХ, равна 4,55%. В результате даже при неизменных значения АХ правило 1-2s может срабатывать в среднем через каждые 22 контрольных измерения.
Вероятность появления события, когда 6 КР подряд будут лежать выше или ниже Хср при неизменных значениях АХ будет равна соответственно 3,13%. Эта величина вероятности означает, что такое событие будет появляться без сбоя в работе АС в среднем через каждые 32 контрольных наблюдения, то есть через каждые 32 или 16 рабочих дней соответственно при одном или двух ежедневных контрольных измерениях. То есть такое событие в виде идущих подряд 6 КР выше или ниже Хср будет повторяться почти в 1,5 реже, чем отклонение КР от Хср более, чем на 2S. Поэтому даже на однократное появление такого события уже стоит обращать внимание, то есть использовать эту комбинацию КР в качестве предупредительного правила.
Теперь рассмотрим ситуацию, когда 7 КР подряд будут все лежать выше или ниже Хср. Вероятность появления такого события при неизменных значениях АХ будет равна 1,56%. Эта величина вероятности означает, что такое событие будет появляться без сбоя в работе АС в среднем через каждые 64 контрольных измерения, то есть через каждые 64 рабочих дня при одном ежедневном контрольном измерении. То есть при неизменных значениях АХ событие в виде 7 КР подряд выше или ниже Хср будет встречаться почти в 3 раза реже, чем срабатывание правила 1-2s. Поэтому даже на однократное появление такого события уже имеет смысл обращать внимание, хотя и использовать его следует видимо только в качестве предупредительного правила.
Продолжая анализ дальше, получим, что вероятность появления в условиях стабильности АХ последовательности из 8 КР подряд, где все они лежат или выше, или ниже Хср, будет в два раза меньше, чем для последовательности из 7 КР подряд, то есть будет равна 0,78%. Эта величина вероятности означает, что такое событие будет появляться без сбоя в работе АС в среднем через каждые 128 контрольных измерений, если такие измерения проводятся один раз в день. И таким образом событие в виде 8 КР подряд выше или ниже Хср будет в условиях стабильности АХ появляться почти в 6 раз реже, чем событие, обуславливающее срабатывание правила 1-2s. Поэтому даже на однократное появление 8 КР подряд выше или ниже Хср точно стоит обращать внимание, а правило на такой основе, по всей видимости, целесообразно включить в промежуточную категорию между предупредительными и контрольными правилами. Назовем такую категорию правил сигнальной. Появление такого события с высокой вероятностью может быть как следствием реального выхода АС из-под контроля, так и ложным срабатыванием правила.
Вероятность появления 9 последовательных КР по одну сторону от Хср при неизменных значениях АХ будет, по всей видимости, в два раза меньше, чем вероятность появления последовательности из 8 КР подряд, то есть будет равна 0,39%. Эта величина вероятности означает, что такое событие даже без сбоев в работе АС может появляться в среднем через каждые 256 контрольных измерения. Появление такого события можно считать уже весьма редким. Поэтому, скорее всего, такое событие следует считать весьма невероятным для условий, когда эксплуатационные значения АХ остаются неизменными. В таком предположении появление подобного события будет сигналом о выходе АС из-под контроля. Соответственно, правило на его основе будем тоже называть сигнальным.
В Таблице 8.1 представлена итоговая информация о вероятностях и частоте срабатывания в условиях стабильности АХ предупредительных, сигнальных и контрольных правил, рассмотренных ранее. Фактически эти вероятности являются вероятностями ложной детекции выхода АС из-под контроля.
Таблица 8.1. Вероятности и частота срабатывания предупредительных (П), сигнальных (С) и контрольных (К) правил в условиях стабильности значений АХ.
| Правила / События | Класс правил | Вероятность появления, % | Средняя частота появления |
| 5Хср | П | 6,25 | через 16 наблюдений |
| 1-2s | П | 4,55 | через 22 наблюдения |
| 6Хср | П | 3,13 | через 32 наблюдения |
| 7Хср | П | 1,56 | через 64 наблюдения |
| 1-2,5s | П | 1,24 | через 81 наблюдение |
| 8Хср | С | 0,78 | через 128 наблюдений |
| 9Хср | С | 0,39 | через 256 наблюдений |
| 1-3s | К | 0,27 | через 370 наблюдений |
| 2-2s | К | 0,10 | через 1000 наблюдений |
| R-4s | К | 0,10 | через 1000 наблюдений |
| 4-1s | К | 0,13 | через 769 наблюдений |
| 10Хср | К | 0,20 | через 513 наблюдений |
Из данных таблицы 8.1 видно, что величины вероятностей ложного срабатывания типовых контрольных правил, то есть их срабатывания в условиях, когда значения АХ при эксплуатации АС остаются на самом деле стабильными, не превышают 0,3%. По всей видимости, эту величину вероятности и следует считать критической при выборе контрольных правил. То есть будем полагать уровень значимости для задач оперативного контроля качества равным 0,3%. В том смысле, что события с вероятностью появления 0,3% и менее для задач мониторинга стабильности АХ следует считать практически невозможными. Поэтому срабатывание контрольных правил в условиях стабильности АХ считают практически невероятным событием. И если такие невероятные события все-таки происходят, то причиной их появления являются, скорее всего, произошедшие ранее сбои в работе АС, приведшие к изменению их АХ.
Соответственно, правила, которые ложно срабатывают при появлении в аналогичных условиях событий, имеющих вероятности от 6,3% и до 0,8%, видимо имеет смысл считать только предупредительными. В том смысле, что их срабатывание может вполне быть обусловлено как произошедшими изменениями в работе АС, так и относительно высокой вероятностью появления соответствующих КР в условиях ее стабильной работы. Обратное тоже верно. Так, например, если правило 1-2s не сработало в текущей аналитической серии, то этот факт вряд ли следует использовать на постоянной основе в качестве критерия приемлемости данной аналитической серии.
Те правила, вероятность ложного срабатывания которых лежит между 0,8% и 0,3%, имеет смысл считать сигнальными, то есть уже не предупредительными, но еще и не контрольными. События, которые сигнализируют о ложном срабатывании правил с вероятностями появления более 0,3%, еще не следует относить к маловероятным событиям при решении рассматриваемых в этой лекции задач. Поэтому появление соответствующих КР следует считать еще допустимыми при ведении мониторинга стабильности АХ АС.
Также следует отметить, что, с точки зрения количества КР, формирующих то или иное правило, наиболее чувствительным к появлению заметных изменений в эксплуатационных значениях АХ является предупредительное правило 1-2s, поскольку для его срабатывания требуется только 1 КР. Наиболее чувствительным для детекции произошедшего изменения эксплуатационного значения стандартного отклонения является контрольное правило R-4s, а для детекции произошедшего изменения эксплуатационного значения систематического смещения – контрольное правило 2-2s, поскольку для их срабатывания требуются только 2 КР. Соответственно, наиболее чувствительным к факту изменения полной ошибки является контрольный признак 1-3s.
Ввиду того, что не все контрольные и даже не все предупредительные признаки могут проявляться одновременно при статистически значимых, то есть фактически произошедших изменениях эксплуатационных значений АХ, необходимо вести мониторинг стабильности АХ с использованием всех типовых контрольных правил, дабы не пропустить сам факт произошедших изменений. Например, контрольные правила 4-1s и 10Хср, сигнализирующие об изменении систематического смещения, могут проявиться оба сразу или раздельно и без срабатывания даже самого чувствительного к произошедшим изменениям АХ правила – правила 1-2s.
Также следует отметить, что при использовании изложенных выше технологий мониторинга стабильности АХ возможны случаи детекции произошедших изменений АХ, не столь существенно влияющих на точность проведенных измерений, чтобы браковать результаты по пациентам. Действительно, если после произошедших изменений и новые эксплуатационные значения АХ остаются в пределах установленных норм точности, то нет никакой необходимости отбраковывать результаты по пациентам аналитической серии, в которой был получен КР, приведший к срабатыванию какого-либо контрольного правила. Это достаточно серьезный недостаток традиционных технологий. Суть этого недостатка состоит в том, что в традиционных технологиях срабатыванием контрольных правил фиксируется факт произошедшего изменения эксплуатационного значения АХ, но не учитывается его величина в сравнении с имеющимся запасом прочности АС по точности. В традиционных технологиях мониторинга стабильности АХ вообще не используются понятия ни меры запаса точности АС, ни меры величины произошедшего изменения ее АХ. По этой причине в таких технологиях отсутствует механизм разделения произошедших изменений АХ на существенные и несущественные. Такое разделение стало осуществляться в современных технологиях мониторинга стабильности АХ. О новых технологиях мониторинга стабильности АХ, учитывающих запас прочности АС по правильности, речь пойдет в следующей лекции.
В заключение этой лекции отметим, что помимо ведения оперативного контроля качества с использованием КМ очень разумно одновременно с ним вести оперативный контроль на базе ежедневных средних по пациентам (далее – ЕСПП). При ведении контроля на базе ЕСПП в качестве образцов высокостабильного биоматериала используют виртуальные (условные) пулы, которые формируются из числа проб пациентов, проанализированных в течение текущего рабочего дня. Пробы включают в виртуальный пул, если результаты их анализа близки к нормальным и попадают в определенный диапазон. В качестве результата измерения уровня аналита в таком виртуальном пуле текущего дня используют среднее значение результатов проб, включенных в пул. Границы диапазона, на основании которого проанализированные за день пробы отбирают в пул, устанавливают по определенному алгоритму. Обычно диапазон для отбора проб получается несколько шире референтного диапазона. Опыт показал, что при правильной установке границ для отбора, средние за день значения результатов анализа отобранных проб оказываются распределенными по нормальному закону. Конечно, при условии, что и АХ АС, и процедуры преаналитического этапа будут оставаться стабильными изо дня в день. Ведение оперативного контроля на базе ЕСПП одновременно с оперативным контролем на базе КМ позволяет отделять реальные сбои в работе АС от проблем, возникающих на преаналитическом этапе. Если изо дня в день никаких существенных изменений АХ АС и процедур преаналитического этапа не происходит, то ни один из этих контролей не будет указывать на сбой в работе АС. Но, если по итогам рабочего дня оперативный контроль на базе КМ не указывает на наличие сбоя, а оперативный контроль на базе ЕСПП указывает на это, то возникновение такой ситуации обычно связано с проблемами, произошедшими на преаналитическом этапе.
Краткие выводы по Лекции 8.
- В традиционных технологиях оперативного контроля качества в качестве детекторов произошедших изменений эксплуатационных значений аналитических характеристик используются контрольные правила, по факту срабатывания которых судят о выходе аналитической системы из-под контроля.
- Контрольные правила формируются на базе комбинаций контрольных результатов, появление которых считается практически невозможным событием в случае сохранения эксплуатационных значений аналитических характеристик неизменными. Уровень значимости при решении задач оперативного контроля устанавливается вблизи 0,3%.
- обычно используют одно контрольное измерение уровня аналита в одном или в двух контрольных материалах в каждой аналитической серии или в течение рабочего дня. Это позволяет экономить время и средства.
- Экономия на количестве контрольных измерений в серии при ведении оперативного контроля по традиционным технологиям с использованием типовых контрольных правил зачастую не позволяет детектировать произошедшие изменения аналитических характеристик в режиме реального времени, поскольку для срабатывания большинства правил требуется наличие двух и более контрольных результатов, полученных после выхода АС из-под контроля.
- В традиционных технологиях отсутствует механизм блокировки срабатывания контрольных правил при несущественных изменениях аналитических характеристик, после которых их эксплуатационные значения остаются в пределах установленных норм точности.
Литература к Лекции 8.
- Приказ МЗ РФ от 07.02.2000 №45 «О системе мер по повышению качества клинических лабораторных исследований в учреждениях здравоохранения РФ». Приложение 2. «Правила проведения внутрилабораторного контроля качества количественных лабораторных исследований».
- Приказ МЗ РФ от 26.05.2003 №220 «Об утверждении отраслевого стандарта «Правила проведения внутрилабораторного контроля качества количественных методов клинических лабораторных исследований с использованием контрольных материалов». Приложение. «ОСТ 91500.13.0001-2003».
- Гмурман В.Е. Теория вероятностей и математическая статистика: учебное пособие для вузов. Девятое издание, стереотипное. М.: Высшая школа, 2003.
- https://lumpics.ru/laplace-function-in-excel
- http://kvm.gubkin.ru/pub/fan/laplasetable2.pdf


