М.И.Прищепа, кандидат технических наук, ЗАО «АНАЛИТИКА»
В данной лекции будут рассмотрены два вопроса: во-первых, в какой степени величина прецизионности аналитической системы (далее — АС) может влиять на точность ее калибровки, то есть на величину ее систематического смещения, и, во-вторых, насколько и каким образом величину этого смещения можно уменьшать, если в этом возникнет необходимость. Интуитивно вроде бы и так понятно, что чем хуже прецизионность АС, тем менее точной будет и калибровка, и тем больше будет величина систематического смещения у АС после проведения калибровочных процедур. Тем не менее, обычно не находится ясных ответов на вопросы в какой степени из-за низкой прецизионности АС могут быть пагубны последствия для величины смещения в результате ее типичной калибровки. И возникают ли реально эти пагубные последствия вообще. А если возникают, то при каких условиях. Из-за отсутствия ясных ответов на эти вопросы обычно, в том числе и чтобы сэкономить, при проведении калибровки ограничиваются однократными измерениями в калибраторе физической величины, которая непосредственно и однозначно характеризует содержание исследуемого аналита в пробе. Такой физической величиной, например, является оптическая плотность конечного продукта биохимической реакции. Собственно говоря, в данной лекции и будут разбираться вопросы всегда ли при калибровке допустимо однократно измерять такую физическую величину. И, соответственно, если не всегда, то при каких условиях уже нельзя ограничиваться однократными измерениями ее оптической плотности в калибраторе. После рассмотрения этих вопросов станет ясно, когда можно экономить на кратности измерений при проведении калибровки, а когда – нет и почему.
Напомним, что основная цель калибровки состоит в проведении измерительных процедур, позволяющих установить взаимно однозначное соответствие между физической величиной, непосредственно измеряемой на АС, с уровнем искомого аналита, который и определяется с ее помощью, но непосредственно на АС не измеряется. Например, установить соответствие между оптической плотностью конечного продукта биохимической реакции, непосредственно измеряемой фотометрическим блоком АС, с содержанием аналита в анализируемой биопробе, для определения чего в конечном итоге и предназначена данная АС. В большинстве случаев на практике такие задачи решаются путем передачи АС информации о размере содержания анализируемого аналита, однозначно соответствующего размеру физической величины, измеряемой непосредственно на АС. Для практической реализации такой передачи используют зачастую один или несколько калибраторов, роль которых играют или эталоны или стандартные образцы с заранее установленным содержанием исследуемого аналита. Затем физической величине, измеренной в калибраторе, приписывают то самое заранее установленное содержание в нем исследуемого аналита. По окончании калибровочных процедур на основании полученных данных для АС строится и/или запоминается в ней калибровочный график, представляющий собой зависимость содержания аналита в биопробе от непосредственно измеряемой на АС физической величины, например оптической плотности конечного продукта биохимической реакции. Такой калибровочный график позволяет однозначно определять содержание искомого аналита в биопробах в пределах всего диапазона измерений, установленного для используемой АС. Если калибровочная зависимость в пределах диапазона измерений АС представляет собой линейную функцию, то обычно для проведения калибровки обходятся двумя или даже одним калибратором. Такие калибровки называют соответственно двухточечными и одноточечными.
В качестве справки следует отметить, что в Статье 1 Главы 18 Федерального закона об обеспечении единства измерений [1] указывается, что «…калибровка … должна выполняться с использованием эталонов единиц величин, прослеживаемых к государственным первичным эталонам соответствующих единиц величин, а при отсутствии соответствующих государственных первичных эталонов единиц величин — к национальным эталонам единиц величин иностранных государств». Из этой цитаты следует, что при проведении калибровки закон допускает использование эталонов иностранных государств. В этой лекции мы не будем касаться вопросов наличия для практического применения тех или иных эталонов единиц величин, определяемых в лабораторной медицине. Будем предполагать, что они уже все имеются в наличии. Хотя это и не совсем так. Нас далее будет интересовать только вопрос, каким образом можно проводить калибровку АС с нужной точностью.
Как уже упоминалось выше, интуитивно понятно, что чем меньше коэффициент аналитической вариации у АС, тем точнее можно осуществлять ее калибровку, то есть более точно задать значения калибровочной функции: калибровочной прямой или в общем случае – калибровочной кривой. Действительно, если на АС осуществляется одноточечная или двухточечная калибровка, что на практике встречается достаточно часто, то результаты измерения непосредственно измеряемой на АС физической величины, например оптической плотности, в первом (с меньшим уровнем аналита) и втором (с большим уровнем аналита) калибраторах будут тем ближе к их фактическим значениям, чем лучше будет воспроизводимость у результатов измерений. Достаточно очевидно также, что если калибровочная зависимость линейная, то воспроизводимость результатов измерений непосредственно измеряемой на АС физической величины, например, оптической плотности конечного продукта реакции, и воспроизводимость результатов определения содержания искомого аналита будут одинаковы (для их относительных единиц).
Так, например, если при фотометрировании на АС конечного продукта реакции выполнятся закон Бугера-Ламберта-Бера, то оптическая плотность и концентрация поглощающего вещества в растворе связаны линейно, то есть оптическая плотность A будет пропорциональна концентрации C. Соответственно концентрация искомого аналита будет вычисляться по формуле: С = А / (k*l), где k – удельный показатель поглощения аналита, а l – длина оптического пути. Для определения содержания аналита фотометрическим методом обычно используют эталон или стандартный образец с известным содержанием искомого аналита. Последующий расчет концентрации основан на использовании соотношения: С/Со = А/Ао или С = Со*A / Ао, где С и Со – соответственно искомая концентрация и концентрация аналита в стандартном образце/эталоне, а А и Ао – оптические плотности соответственно анализируемой биопробы и стандартного образца/эталона. Отсюда следует, что в относительных единицах воспроизводимость результатов измерений непосредственно измеряемой на АС физической величины, то есть оптической плотности А, и воспроизводимость результатов определения содержания С искомого аналита будут одинаковы. То есть воспроизводимость результатов целиком и полностью определяется свойствами АС, внутренне ей присущими, и условиями ее эксплуатации. То есть каким будет коэффициент вариации результатов измерения оптической плотности, таким будет и коэффициент вариации результатов определения концентрации аналита и наоборот. Остается открытым вопрос о правильности результатов, которая, как упоминалось выше, зависит от точности калибровки АС, что в конечном счете влияет на величину ее систематического смещения.
Попробуем на вероятностном языке на нескольких конкретных примерах оценить влияние коэффициента вариации АС на точность ее калибровки, вернее на величину ее систематического смещения. Как и в предыдущих лекциях, обозначим относительное значение систематического смещения АС при ее эксплуатации как Вас,%, его предельно допускаемое значение (далее — ПДЗ) как Ва,%, соответственно эксплуатационное значение коэффициента вариации АС обозначим как CVac, а его ПДЗ — как CVа. Напомним, что ПДЗ для CVac и Bac,% вычисляются по формулам:
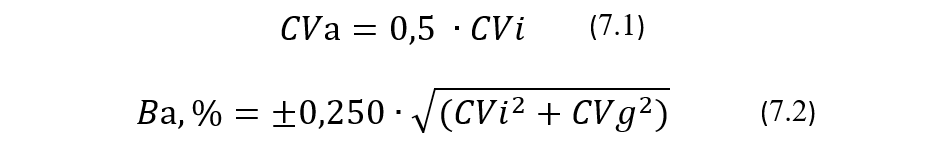
где CVi и CVg — коэффициенты соответственно внутри- и межиндивидуальной биологической вариации.
Для простоты рассмотрим в качестве примера биохимический метод с одним калибратором и фотометрированием продукта реакции по конечной точке, а именно рассмотрим определение концентрации глюкозы в сыворотке глюкозооксидазным методом. Как известно, суть этого метода состоит в окислении глюкозы под действием глюкозооксидазы с промежуточным образованием перекиси водорода, которая в свою очередь реагирует в присутствии пероксидазы с фенолом и 4-аминофеназоном с образованием хинонимина как конечного продукта реакции. Последний, собственно, и фотометрируется. Обычно в типовых реализациях этого метода ограничиваются одним калибратором, в качестве которого используют стандартный водный раствор глюкозы с концентрацией 5,55 ммоль/л. То есть с уровнем глюкозы вблизи верхней границы референтного диапазона. Будем полагать, что ошибки определения концентрации глюкозы в стандартном образце и воспроизведения им этой концентрации при проведении калибровки существенно меньше величины CVac. Напомним также, что, коэффициент вариации АС может не оставаться постоянным даже в пределах ее диапазона измерений. То есть, если в методе используется для калибровки два калибратора с разными уровнями аналита, то следует оценивать влияние коэффициента вариации АС на величину ее систематического смещения для каждого из калибраторов.
Теперь сначала предположим, что при калибровке АС проводятся однократные измерения оптической плотности Ао единственного калибратора, то есть стандартного образца глюкозы с заранее аттестованной концентрацией Со, указанной в его паспорте. С учетом этого предположения оценим, как будет сказываться величина коэффициента вариации CVac на величине систематического смещения Вас,% при однократном измерении оптической плотности конечного продукта реакции в калибраторе, соответствующей аттестованному в нем уровню глюкозы. Для оценки степени влияния прецизионности АС на величину ее смещения в результате проведенной калибровки будем использовать относительные величины возможных отклонений результатов измерений оптической плотности (далее ОП) калибратора, причем в двух видах: в виде ожидаемого в среднем отклонения, и в виде максимально возможного с 95% вероятностью отклонения, то есть в виде верхней границы 95% доверительного интервала для всех возможных отклонений. Поскольку в лабораторной диагностике общепринято иметь 95% уровень доверия, то тогда в общем-то понятно, что надо улучшить воспроизводимость результатов определения ОП калибратора настолько, чтобы величина систематического смещения не превышала своего ПДЗ в 95% калибровочных случаев.
Величину ожидаемого в среднем отклонения будем рассчитывать, учитывая доли результатов измерений оптической плотности, которые будут отклоняться от ее фактического значения и попадать в границы отрезков, длина которых кратна целому стандартному отклонению σ или его доли, то есть либо σ, либо σ/2, либо σ/4 и т.д. Такой подход к усреднению еще называют усреднением с учетом статистического веса случайной величины на том или ином отрезке ее значений. Для простоты восприятия этого подхода воспользуемся известными о нормальном распределении данными о том, что 68,3% значений случайной величины находятся на расстоянии не более одного стандартного отклонения σ от среднего; 95,5% значений – не более двух стандартных отклонений, из которых 27,2% значений отклоняются от среднего свыше одной σ, но не более двух σ и, наконец 99,7% – не более трёх σ, из которых 27,2% значений отклоняются от среднего свыше одной σ, но не более двух σ, а 4,2% значений отклоняются от среднего свыше двух, но не более трех σ. Заметим, что этот факт является частным случаем так называемого правила трёх сигм для выборок из нормального распределения. Исходя их этого можно грубо предположить, что 68,3% результатов измерений оптической плотности будут в среднем отклоняться от своего фактического значения точно на 0,5σ, соответственно 27,2% – в среднем точно на 1,5σ, и, наконец, 4,2% – в среднем точно на 2,5σ. Это будет означать, что из 1000 результатов 683 отклонятся в среднем на 0,5σ от своего фактического значения, 272 – отклонятся в среднем на 1,5σ и, наконец, 42 – отклонятся в среднем на 2,5σ от своего фактического значения. Теперь определим среднее значение ∆ср всех этих отклонений. Собственно, это среднее значение и будет являться ожидаемым в среднем отклонением:
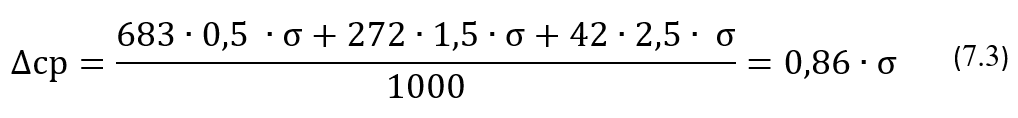
Соответственно, для вычисления относительного значения ∆ср,% ожидаемого в среднем отклонения получим следующую формулу:
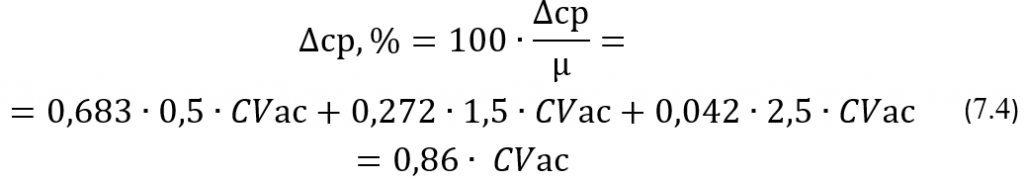
Для более точных оценок величины ожидаемого в среднем отклонения потребуется в несколько раз увеличивать количество отрезков усреднения, уменьшая их длину. То есть вместо выше использованных отрезков усреднения, длина которых была кратна σ, надо будет использовать отрезки, длина которых будет кратна, например, половине σ или одной ее четверти, или одной ее восьмой или еще меньше, в зависимости от желаемой точности оценки. Кроме того, надо будет, используя так называемую интегральную функцию Лапласа, вычислить вероятности P (xi<x<xi+1) попадания случайной величины х, то есть результатов измерений, в границы каждого i-того отрезка усреднения (хi; хi+1) по следующей формуле:
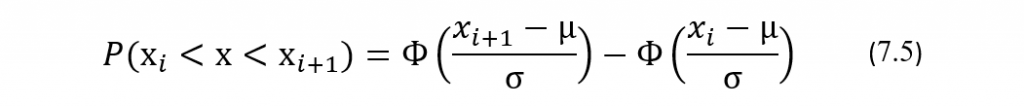
где i=1,2,3,… – номера отрезков усреднения, µ — математическое ожидание (среднее значение) случайной величины х, а Ф((x-μ)/σ) интегральная функция Лапласа, которую в элементарных функциях представить нельзя, но для значений которой составлены таблицы, которые широко представлены в интернете, см., например, сайт [3]. Вычисления вероятности попадания случайной величины х в выбираемой отрезок усреднения с границами хi и хi+1 с помощью таблиц проводятся, как будет видно из следующего абзаца, достаточно просто, не вызывая никаких затруднений.
Также отметим, что использование этих таблиц позволяет легко вычислить вероятность того, что результат измерения ОП в калибраторе как некая случайная величина х отклонится от своего фактического значения не свыше ожидаемого в среднем отклонения: Р(µ-0,86µ < x< µ+0,86σ) = 2*Р(µ< x< µ+0,86σ) = 2*[Ф(0,86) – Ф(0,00)] = 2*(0,305 – 0) = 2*0,305 = 0,61 или 61,00%. Соответственно результаты измерения ОП будут лишь в 39% случаев отклоняться от своего фактического значения свыше ожидаемого в среднем отклонения. Использование множителя 2 обусловлено тем, что нормальное распределение симметрично относительно своего математического ожидания (в данном случае фактического значения ОП в калибраторе), а результаты измерения ОП могут отклоняться от своего фактического значения как в большую, так и в меньшую сторону.
Теперь вычислим, используя табличные значения функции Лапласа, приведенные в [3], и формулу (7.5), вероятности попадания результатов измерения ОП в калибраторе в пределах µ и µ+3σ в отрезки, длина которых кратна σ/2, что будет соответствовать изменению индекса i от 1 до 6, а затем оценим с их помощью величину ожидаемого в среднем отклонения. Итак, вероятность случайной величине х попасть в интервал (х1=µ; х2=µ+0,5σ) будет равна Р(µ < x < µ+0,5σ) = Ф(0,50) – Ф(0,00) = 0,1915 — 0 = 0,1915 или 19,15%. Вероятность случайной величине попасть в интервал (х2=µ+0,5σ; х3=µ+1,0σ) будет равна Р(µ+0,5µ < x < µ+1,0σ) = Ф(1,00) – Ф(0,50) = 0,3413 — 0,1915 = 0,1498 или 14,98%. Далее, вероятность случайной величине попасть в интервал (х3=µ+1,0σ; х4=µ+1,5σ) будет равна Р(µ+1,0µ < x < µ+1,5σ) = Ф(1,50) – Ф(1,00) = 0,4332 — 0,3413 = 0,0919 или 9,19%. Вероятность случайной величине попасть в интервал (х4=µ+1,5σ; х5=µ+2,0σ) будет равна Р(µ+1,5µ < x < µ+2,0σ) = Ф(2,00) – Ф(1,50) = 0,4772 — 0,4332 = 0,044 или 4,40%, а вероятность случайной величине попасть в интервал (х5=µ+2,0σ; х6=µ+2,5σ) будет равна
Р(µ+2,0µ < x < µ+2,5σ) = Ф(2,50) — Ф(2,00) = 0,4938 — 0,4772 = 0,0166
или 1,66%. И, наконец, вероятность случайной величине попасть в интервал (х6=µ+2,5σ; х7=µ+3,0σ) будет равна Р(µ+2,5µ < x < µ+3,0σ) = Ф(3,00) – Ф(2,50) = 0,4987 — 0,4938 = 0,0049 или 0,49%. Тогда, учитывая симметрию нормального распределения, то есть тот факт, что перечисленные выше вероятности попадания надо удваивать, поскольку вышеупомянутые и симметричные им отрезки располагаются и слева и справа от математического ожидания µ, получим в более точном приближении для величины ожидаемого в среднем отклонения следующую формулу:
∆ср = (2*0,1915*0,25*σ + 2*0,1498*0,75*σ + 2*0,0919*1,25*σ + 2*0,044*1,75*σ + 2*0,0166*2,25*σ + 2*0,0049*2,75*σ) = 0,806*σ. Соответственно, для более точного расчета относительного значения ∆ср,% ожидаемого в среднем отклонения получим следующую формулу:
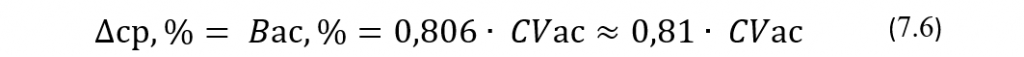
Это более точная оценка относительного значения ∆ср,% ожидаемого в среднем отклонения, чем его оценка с использованием формулы (7.4), хотя они достаточно близки друг ко другу. Их отличие между собой не превышает 6%. В принципе, при возникновении желания увеличить точность оценки путем уменьшения длины отрезков надо будет выбирать их длину, равной уже не половине сигмы, а четверти сигмы. Это может по приведенной выше схеме попробовать сделать каждый желающий в качестве тренировки.
Хотя интуитивно и понятно, что ожидать существенного улучшения точности оценки ожидаемого в среднем отклонения вряд ли при этом следует.
На Рис. 7.1 представлена зависимость систематического смещения Вас,% (на уровне глюкозы в калибраторе) от эксплуатационных значений коэффициента варации CVac после проведения одноточечной калибровки АС с однократным измерением ОП в калибраторе. Расчет ожидаемых в среднем отклонений проводился по формуле (7.6). Данные по ПДЗ были взяты из таблицы на сайте Дж.Вестгарда [2], что составило для CVa = 2,80%, для Ba,% = 2,34 %. Напомним, что из формулы (7.6) следует, что в таких случаях ожидаемое в среднем отклонение результатов от фактического значения измеряемой величины будет равно 0,81*CVac, завися только от конкретного значения CVac. Как видно из Рис.7.1, относительное значение систематического смещения при таком среднем отклонении результатов не будет в среднем превышать своего ПДЗ. Соответственно максимально возможное в относительных единицах отклонение результата измерения от своего фактического значения на 95% уровне доверия составит величину 1,96*СVac, что равно верхней границе 95% доверительного интервала для математического ожидания результатов измерений, то есть верхней границе 95% доверительного интервала для фактического значения измеряемой физической величины. Из Рис. 7.1 так же видно, что в случае АС для определения концентрации глюкозы в сыворотке ПДЗ для систематического смещения будет после калибровки в среднем достигаться только при эксплуатационном значении CVac, близком к своему ПДЗ, то есть к значению СVa. Но для того, чтобы с 95% надежностью величина систематического смещения после калибровки не превышала своего ПДЗ эксплуатационное значение CVac (вернее воспроизводимость результатов однократных измерений ОП) не должно превышать 40% своего ПДЗ.
Из лабораторной практики известно, что у большинства АС, включая АС для определения концентрации глюкозы в сыворотке, эксплуатационные значения коэффициента вариации CVac обычно близки к его ПДЗ. Следовательно, проводить в таких случаях калибровку с однократным измерением ОП калибратора не имеет особого смысла, поскольку тогда после такой калибровки величина систематического смещения АС с большой вероятностью окажется вблизи или выше своего ПДЗ. В таких случаях весьма разумно улучшить воспроизводимость результатов измерений ОП в калибраторе.
В предыдущей лекции (см. Лекцию 6) упоминалось, что воспроизводимость результатов измерений на АС можно улучшать при одном и том же ее значении CVac за счёт увеличения кратности измерений. Точнее говоря, при увеличении кратности измерений в n раз коэффициент вариации усредняемых результатов будет уменьшаться в корень квадратный из n раз. Например, если однократные измерения той или иной физической величины в биопробе заменить на четырехкратные, то есть измерять физическую величину не один раз, а четыре раза подряд и в качестве итогового результата брать среднее значение этих четырёх результатов повторных измерений, то тогда коэффициент вариации таких итоговых результатов будет в два раза меньше, чем коэффициент вариации однократных измерений.
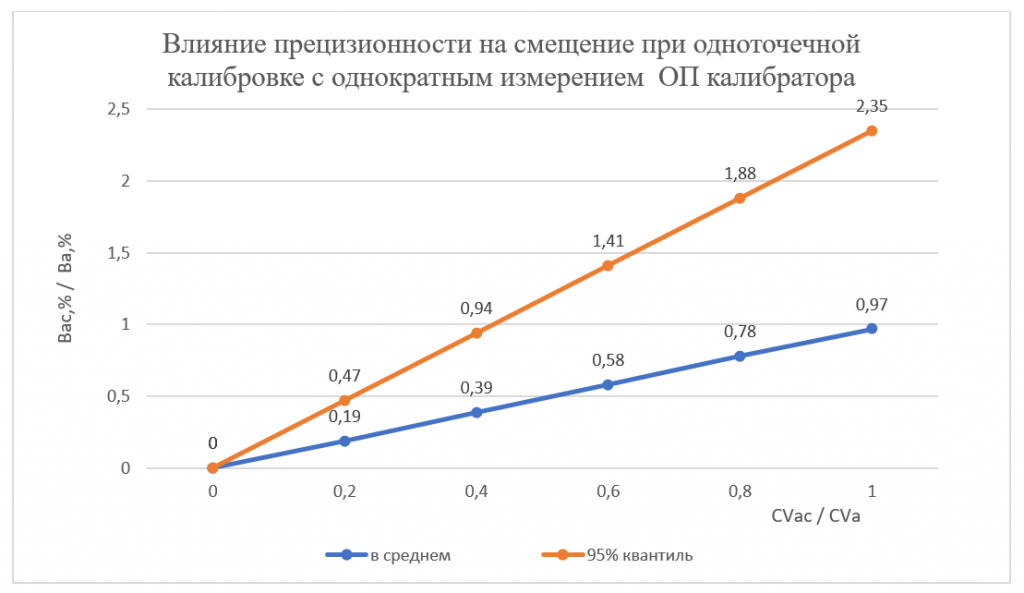
Рис. 7.1. Зависимость величины систематического смещения Вас,% на уровне глюкозы в калибраторе от величины прецизионности CVac после проведения одноточечной калибровки.
Количество измерений оптической плотности калибратора – 1. Смещение на уровне глюкозы 0 ммоль/л равно 0%. ПДЗ для смещения Ва,%=2,34. ПДЗ для прецизионности СVa=2,8%.
Соответственно коэффициент вариации результатов девятикратных измерений будет в три раза меньше, чем коэффициент вариации результатов однократных измерений.
Отсюда следует, что если при калибровке АС проводить не однократные, а четырехкратные измерения ОП в калибраторе, то воспроизводимость усредненных результатов будет в 2 раза лучше. При четырехкратном измерении ОП в калибраторе относительную величину ∆ср,% ожидаемого в среднем отклонения таких усредненных результатов тогда следует вычислять по следующей формуле:
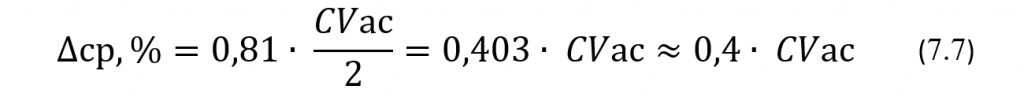
На Рис 7.2 представлена зависимость систематического смещения Вас,% АС (на уровне глюкозы в калибраторе) от коэффициента вариации CVac с четырехкратным измерением ОП в калибраторе. Из этого рисунка и из формулы (7.7) следует, что при такой кратности измерения ОП в калибраторе ожидаемое в среднем отклонение результатов измерения оптической плотности от его фактического значения составит величину, близкую к 0,4*CVac. При этом величина систематического смещения после такой калибровки в среднем будет достигать только 20% своего ПДЗ. В то же время, с 95% достоверностью величина систематического смещения не будет достигать своего ПДЗ после калибровки только при эксплуатационных значениях CVac менее 80% своего ПДЗ. При значениях CVac, близких к CVa, величины Вас,% после калибровки могут превышать свой ПДЗ и достигать величины 1,17*Ва,% при CVac=CVа.
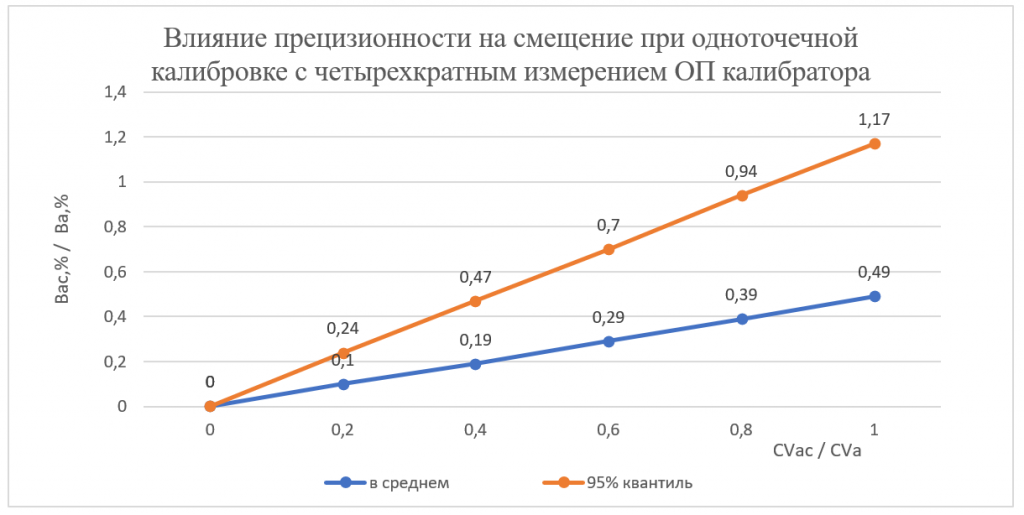
Рис. 7.2. Зависимость величины систематического смещения Вас,% на уровне глюкозы в калибраторе от величины прецизионности CVac после проведения одноточечной калибровки.
Количество измерений оптической плотности калибратора – 4. Смещение на уровне глюкозы 0 ммоль/л равно 0%. ПДЗ для смещения Ва,%=2,34. ПДЗ для прецизионности СVa=2,8%.
Для наглядности на Рис. 7.3 и Рис. 7.4 представлены зависимости систематического смещения Вас,% от коэффициента вариации CVac после проведения калибровки соответственно с пятикратным и шестикратным измерением ОП в калибраторе. Как видно из этих рисунков, только после шестикратного измерения ОП в калибраторе можно будет с 95% уверенностью полагать, что величина систематического смещения у АС для определения глюкозы в сыворотке глюкозооксидазным методом не превысит свое ПДЗ, если конечно эксплуатационное значение CVac тоже не превысит свое ПДЗ.
Как было упомянуто выше, оценивать величину систематического смещения после калибровки надо для каждого калибратора, если их больше одного.
В любом случае, если же все таки ставить цель, чтобы в результате калибровки АС получаемое значение систематического смещения с 95% вероятностью не превышало свое ПДЗ, то вполне возможно за счет увеличения кратности измерений N добиваться того, чтобы относительное значение верхней границы доверительного интервала для относительного значения матожидания измеряемой величины становилось меньше ПДЗ для относительного значения систематического смещения, то есть чтобы 1,96*CVac / √N ≤ Ва,%.
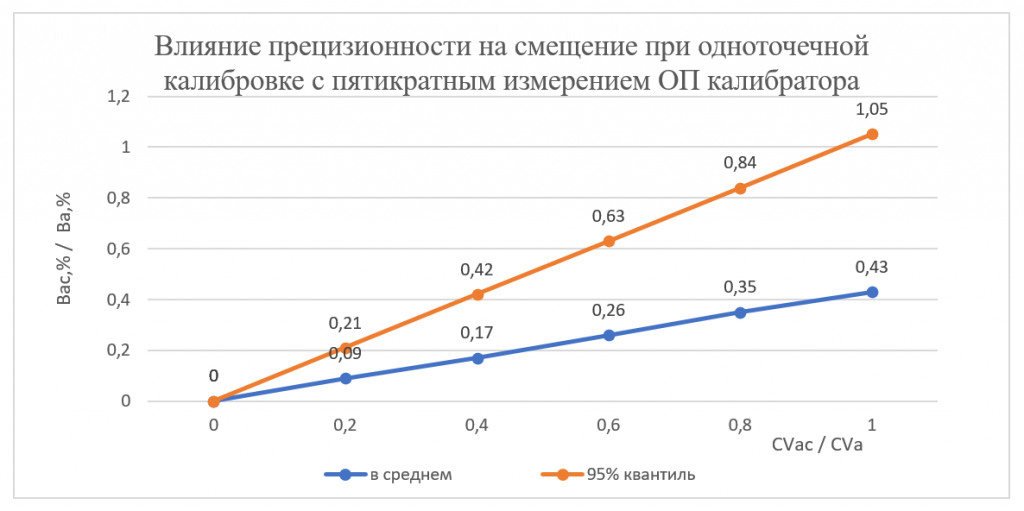
Рис. 7.3. Зависимость величины систематического смещения Вас,% на уровне глюкозы в калибраторе от величины прецизионности CVac после проведения одноточечной калибровки.
Количество измерений оптической плотности калибратора – 5.
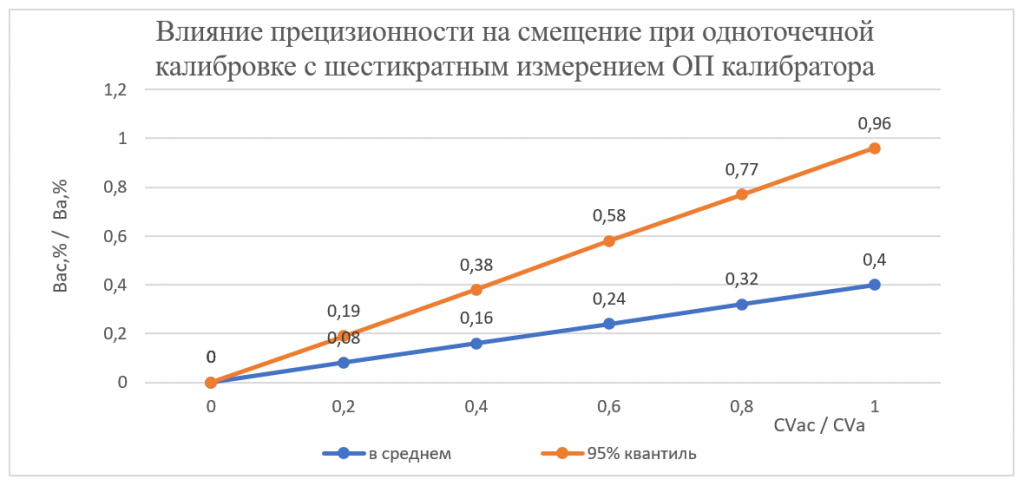
Рис. 7.4. Зависимость величины систематического смещения Вас,% на уровне глюкозы в калибраторе от величины прецизионности CVac после проведения одноточечной калибровки.
Количество измерений оптической плотности калибратора – 6.
Тогда для вычисления минимальной кратности N измерения в калибраторе физической величины, непосредственно измеряемой АС, получим формулу:
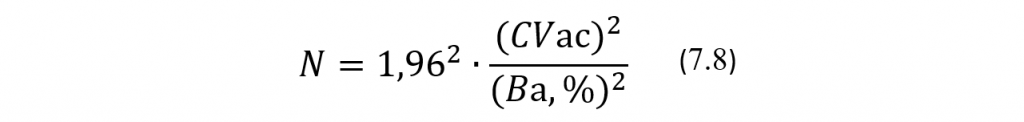
В качестве примера вычисления N по этой формуле воспользуемся данными для АС, предназначенной для определения содержания глюкозы в сыворотке. Предположим также, что эксплуатационное значение CVаc=CVa, что соответствует обычной для определения уровней глюкозы практике. Тогда получим: N= (1,96)2*(CVa)2 / (Ba,%)2 = 3,84*7,84 / 5,48=5,5≈6. То есть при калибровке типовой АС для определения уровней глюкозы кратность измерения ОП в калибраторе должна быть равна 6, если эксплуатационное значение коэффициента вариации близко к своему ПДЗ. Примеры вычислений кратности измерений N при проведении калибровки АС для определения некоторых других аналитов приведены в Таблице 7.1, причем в зависимости от величины эксплуатационного значения CVac по отношению к своему ПДЗ.
Таблица 7.1. Значения кратности измерения N при проведении калибровки
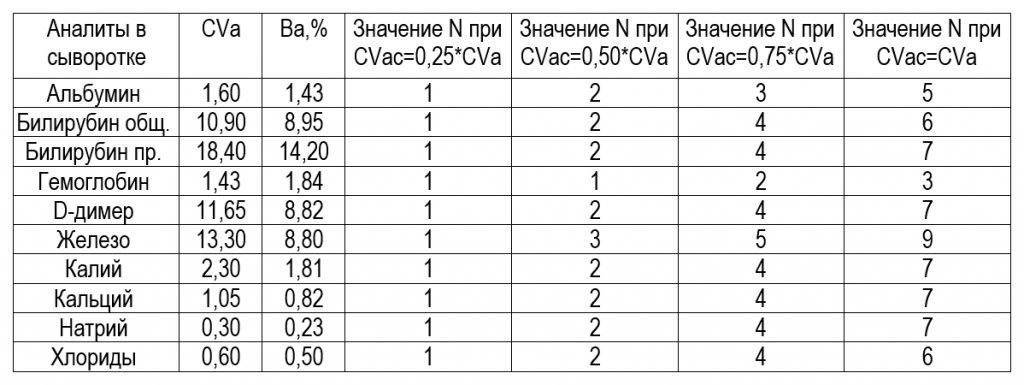
Как видно из Таблицы 7.1, при калибровке АС для определения перечисленных аналитов кратность измерений в калибраторе должна быть в большинстве случаев равна 7, если эксплуатационное значение коэффициента вариации CVac близко к своему ПДЗ, равна 4, если CVac близко к 75% своего ПДЗ, и равна 2, если CVac близко к 50% своего ПДЗ.
Краткие выводы по Лекции 7.
- Величина прецизионности АС в процессе проведения калибровки может существенно сказываться на качестве калибровки, влияя на величину систематического смещения АС.
- Точность калибровки можно улучшить за счет увеличения кратности измерений физической величины в калибраторе, непосредственно измеряемой при калибровке.
- Для большинства типовых АС калибровки с однократным измерением физической величины будут приводить к превышению систематическим смещением своего ПДЗ.
- В случаях, когда коэффициент вариации АС близок к своему ПДЗ, что обычно бывает на практике, кратность измерений измеряемой на АС физической величины в калибраторе должна быть в большинстве случаев не менее 7 раз.
Литература к Лекции 7.
- «Об обеспечении единства измерений». Федеральный закон № 102-ФЗ от 26.06.2008.
- https://www.westgard.com/biodatabase1.htm
- www.kvm.gubkin.ru/pub/fan/laplasetable2.pdf


