М.И.Прищепа, кандидат технических наук, ЗАО «АНАЛИТИКА»
В настоящей лекции будут рассмотрены алгоритмы принятия решения о вводе в эксплуатацию аналитической системы, либо ранее не эксплуатируемой в лаборатории, либо в которой одна или несколько ее основных частей подверглись замене или ремонту.
Для принятия решения о возможности запуска в эксплуатацию новой или обновленной аналитической системы (далее — АС) прежде всего необходимо убедиться, что ее аналитические характеристики (далее — АХ) соответствуют установленным нормам. Для этого эксплуатационные значения АХ сравнивают с их предельно допускаемыми. Это общий подход, широко признанный в лабораторной диагностике. Критерий соответствия АХ нормам заключается в следующем: генеральные эксплуатационные значения основных аналитических характеристик не должны превышать установленных для них предельно допускаемых значений или, говоря иным языком, — установленных норм. Как уже упоминалось в предыдущих лекциях, конкретная АС при ее эксплуатации в одних и тех же условиях обладает одними и теми же генеральными значениями АХ. Поскольку определять эти генеральные значения весьма затратное дело, а главное, как это станет ясно в дальнейшем, в этом нет никакой необходимости, то на практике проводят их выборочные оценки, получая вместо генеральных их оценочные значения. Напомним, что методология такой оценки основана на том, что если на одной и той же АС в одних и тех же условиях измерять достаточно долго (с точки зрения математической статистики) уровень аналита в одной и той же биопробе с неизменными составом и свойствами, то полученные результаты всегда будут распределены по нормальному закону со своим математическим ожиданием и стандартным отклонением. Которые, в свою очередь, целиком и полностью определяются аналитическими свойствами, присущими данной АС, и обусловливают ее АХ. Чем лучше у АС прецизионность, тем меньше стандартное отклонение у распределения результатов и тем ближе они распределяются вокруг своего математического ожидания. В случае АС, близкой к идеальной по прецизионности, полученные на ней результаты не будут практически отличаться друг от друга, совпадая со своим математическим ожиданием. Соответственно, чем точнее проведена калибровка АС, тем лучше будет правильность получаемых результатов, тем ближе математическое ожидание их распределения будет к фактическому содержанию аналита в биопробе. В случае АС, близкой к идеальной по правильности, математическое ожидание полученных на ней результатов не будет практически отличаться от фактического уровня аналита в биопробе. Для получения оценочных значений АХ на АС проводятся так называемые установочные серии измерений уровня аналита в одной и той же биопробе, обычно используя для этого аттестованный контрольный материал (далее — КМ), близкий по свойствам матрицы к реальным биопробам пациентов. Установочная серия проводится как правило в течение 20 рабочих дней и состоит из 20 измерений уровня аналита по одному ежедневно. Рекомендуется проводить установочные серии не на одном, а на двух или трех аттестованных КМ с уровнями аналита, близкими к принятию клинических решений. Необходимость проведения установочных серий на нескольких КМ обусловлена разными обычно эксплуатационными значениями АХ для разных уровней исследуемого аналита. После анализа полученных результатов на отсутствие среди них грубых ошибок, вычисляют для каждого КМ выборочные значения систематического смещения, стандартного отклонения, коэффициента вариации и полной ошибки (которую также называют общей аналитической ошибкой) в качестве оценок генеральных значений АХ. Затем по полученным оценочным значениям вычисляют границы доверительных интервалов для соответствующих генеральных значений. Ширина доверительного интервала для генерального значения каждой АХ, в свою очередь, зависит от выбираемого для него уровня доверия, количества контрольных измерений, результаты которых использовались для получения оценочных значений, прецизионности используемой АС и некоторых других параметров. Обычно в лабораторной медицине используют 95% уровень доверия. Что касается количества контрольных измерений, то в разных рекомендациях их число варьирует от 10 до 30.
В настоящее время ведущие международные организации по стандартизации в лабораторной медицине, такие как CLSI и EFLM, в основном рекомендуют вычислять предельно допускаемые значения на базе внутри- и межиндивидуальных биологических вариаций. База данных по этим вариациям с 1999 по 2014 годы (последнее обновление) поддерживалась Дж.Вестгардом на его сайте [1], а затем, начиная с 2019 года эта база данных стала поддерживаться на сайте EFLM – Европейской Федерации Клинической Химии и Лабораторной Медицины. Данные по предельно допускаемым значениям для относительного систематического смещения, коэффициента вариации и относительной полной ошибки, вычисленные на основе данных о биологических вариациях от 2014 года, до сих пор можно найти на сайте Дж.Вестгарда в очень удобном представлении.
Если вместо генеральных значений АХ АС на практике определяют их выборочные оценки, то значения для внутри- и межиндивидуальных биологических вариаций, приведенные на сайте Дж.Вестгарда и на сайте EFLM, весьма близки к генеральным, поскольку, с точки зрения математической статистики, они получены на основе очень большого числа измерений. Поэтому можно вполне предполагать, что нижняя и верхняя границы их доверительных интервалов практически совпадают с самими этими значениями. На самом деле, конечно же, эти значения периодически уточняются по мере накопления экспериментальных данных, то есть по мере увеличения объема результатов исследований. Но по смыслу их вполне можно считать генеральными значениями или математическими ожиданиями внутри- и межиндивидуальных коэффициентов биологических вариаций уровней аналитов in vivo.
Так предельно допускаемые значения (далее — ПДЗ) АХ АС, обозначаемые как Ва,%, CVa и TEa,%=|Ва,%| +1,65*CVa соответственно для относительного систематического смещения, коэффициента вариации и относительной полной ошибки будут тоже являться генеральными значениями, поскольку они рассчитываются на основе внутри- и межиндивидуальных коэффициентов биологических вариаций, обозначаемых CVi и CVg. Следует иметь ввиду, что на сайте Дж.Вестгарда [1] показатели Ва,%, CVa и ТЕа,% обозначены соответственно как B(%), I(%) и TE(%). Выглядят эти формулы, по которым определяются ПДЗ для так называемого желательного диапазона эксплуатационных значений АХ АС, что общепринято в настоящее время, следующим образом:
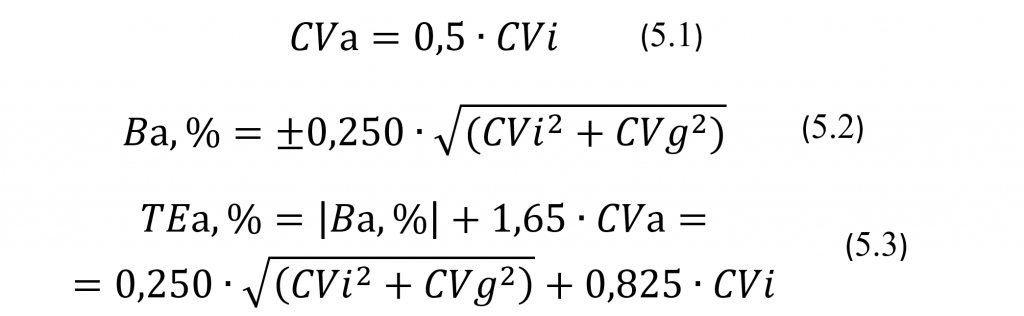
Для этих показателей границы доверительных интервалов нет смысла вычислять с точки зрения рассматриваемых нами вопросов сравнения эксплуатационных значений АХ с их ПДЗ. Поэтому будет полагать, что и нижняя и верхняя границы 95% доверительного интервала совпадают с самим предельно допустимым значением. Именно об этом же идет речь и в пункте 6.1 ГОСТ 53133.1-2008 [2]. Вместе с тем, в пункте 6.2 этого же документа в качестве норм для относительного систематического смещения и межсерийного коэффициента вариации вводятся понятия так называемых оперативных ПДЗ. Оперативные ПДЗ, приведенные в таблице Б.1 документа [2], по сути рассчитываются как верхние границы95% доверительных интервалов для генеральных значений относительного систематического смещения и межсерийного коэффициента вариации некой АС, для которой их оценочные значения как бы были определены либо по 10 либо по 20 контрольным результатам, и оказались равными ПДЗ, рассчитываемым по формулам (5.1) и (5.2).
Следует отметить, что упомянутые выше требования к точности АС на основе биологических вариаций в виде оперативных ПДЗ носят для отечественных лабораторий только справочный характер. Рекомендуемые же нормы перечислены в приказах Минздрава РФ от 07.02.2000 №45 и от 26.05.2003 №220. Они были установлены только для 27 аналитов. Позднее практически без изменений они были перенесены в стандарты [2,3], в которых упоминается, что эти значения для оперативных ПДЗ устанавливались как компромисс между требованиями к АХ АС, установленными на основе данных о биологических вариациях, и данными об измерительных возможностях АС участников ФСВОК (Федеральной Системы Внешней Оценки Качества), полученных более 20 лет назад.
В документе [3] предлагается устанавливать соответствие АХ нормам путем сравнения оценочных эксплуатационных значений основных АХ, вычисляемых по данным соответствующих установочных серий, с рекомендуемыми оперативными ПДЗ. И если полученные оценочные значения относительного смещения и межсерийного коэффициента вариации оказываются больше этих оперативных ПДЗ, то делается вывод, что они не соответствуют установленным нормам. Такой подход, очевидно, несколько смягчает общепринятые международные требования к АХ АС, которые непосредственно вычислены по коэффициентам биологических вариаций уровней аналитов [1]. Так, например, ПДЗ АХ АС для определения содержания глюкозы в сыворотке, вычисленные на основе биологических вариаций по формулам (5.1) – (5.3), будут иметь следующие значения: CVa = 2,80%, Ва,% = ±2,34% и соответственно ТЕа,% = 6,96% [1]. В то время как оперативные ПДЗ, приведенные как справочные в документе [2], имеют приблизительно в полтора большие значения: CV20,%=4,10%, В20,%=±3,90% и соответственно значение ТЕ20,% = |В20,%| +1,65*CV20,% тогда было бы равно 10,67%.
С целью прояснить причины расхождения ПДЗ в упомянутых выше подходах к проверке соответствия эксплуатационных значений АХ АС установленным нормам, в настоящей лекции будет представлен несколько иной, чем в документах [2] и [3], алгоритм проведения этой проверки, базирующийся на сравнении границ доверительных интервалов для генеральных значений АХ АС, определяемых на основе их выборочных оценок, с ПДЗ, рассчитываемых непосредственно по приведенным выше формулам (5.1) – (5.3). В этом подходе сначала, аналогично рекомендациям документа [3], определяются оценочные значения для эксплуатационных АХ АС, включая относительное систематическое смещение Вас,% и межсерийный коэффициент вариации CVас, по которым впоследствии вычисляется относительная полная ошибка ТЕас,%. Для определения оценочных значений используются результаты однократных контрольных измерений уровня аналита в каждой из аналитических серий, количество которых устанавливается в соответствии с выбранными рекомендациями, например или 10 или 20 или 30. Затем с учетом полученных оценочных значений АХ АС, количества контрольных результатов и 95% уровня доверия определяют нижнюю и верхнюю границы соответствующих 95% доверительных интервалов для их генеральных значений. И, наконец, затем сравнивают эти границы с ПДЗ, рассчитываемых по формулам (5.1) – (5.3).
Следует помнить, что при решении задач по проверке соответствия эксплуатационных значений АХ АС установленным нормам, рекомендуется использовать 2 или 3 контрольных материала соответственно с нормальным и патологическими уровнями содержания аналита. Это связано с тем, что практически любая АС в пределах своего диапазона измерений как правило обладает разными, причем статистически значимо отличными друг от друга, значениями аналитических характеристик. Именно поэтому международные и национальные стандарты рекомендуют оценивать эксплуатационные значения АХ АС не на одном, а на двух или на трех уровнях аналита, соответствующих норме, низкой и высокой патологии, если два или все три уровня являются важными для принятия клинических решений. Отсюда следует, что в каждой аналитической серии образцы используемых КМ необходимо анализировать хотя бы по одному разу. Аналитическая серия, как известно [3], определяется в терминах временного промежутка или числа измерений, в течение которых эксплуатационные значения АХ АС существенно не изменяются. Таким образом аналитические серии представляют собой интервалы в виде периодов времени или числа измерений, в пределах которых ожидается, что значения систематического смещения и стандартного отклонения будут оставаться стабильными. Рекомендуемая максимальная продолжительность аналитической серии по времени – 24 часа, а по числу измерений – согласно рекомендациям изготовителей основных составных частей АС и условиям ее эксплуатации [3]. В любом случае продолжительность аналитической серии рекомендуется регулярно переоценивать по мере эксплуатации АС, так как в ней могут проявляться факторы, влияющие на ее АХ, обусловленные либо износом измерительных блоков анализатора, либо деградацией наборов реагентов и калибраторов.
Месторасположение образцов КМ в аналитической серии обычно определяют исходя из того, что контрольные результаты должны быть получены до передачи в клинику результатов по пациентам. Так, например, если в серии проводится анализ проб пациентов поаналитно, то контрольные образцы следует размещать в самом начале и в самом конце серии, для того чтобы обнаруживать возможные изменения в систематическом сдвиге, или размещать их равномерно по длине серии, чтобы следить за возможным дрейфом калибровки, или размещать случайным образом между пробами пациентов для обнаружения случайных ошибок. В любом случае контроли не следует располагать сразу же за образцами калибраторов, поскольку это не позволяет учитывать возможный дрейф или изменение систематического смещения.
Итак, представим, что на внедряемой в эксплуатацию АС было проведено 30 аналитических серий по одной или по несколько в каждый рабочий день, причем в каждой серии измерение уровня аналита проводилось в одном образце (аликвоте) каждого из 2-3 аттестованных контрольных материалов. То есть всего было проведено по 30 измерений в образцах каждого контрольного материала и, соответственно, получено для каждого из них по 30 контрольных результатов (далее – КР). Составим из этих 30 КР три выборки: первая выборка будет состоять из первых 10 КР, вторая — из первых 20 КР, и, наконец, третья – из всех 30 КР. Затем последовательно проведем сравнение эксплуатационных значений АХ, вычисленных с использованием КР каждой выборки, с установленными для них ПДЗ.
Сначала возьмем выборку из первых 10 КР и вычислим на их основе по известным формулам среднее Хср10, стандартное отклонение S10 , систематическое смещение В10 и полную ошибку ТЕ10, положив в нижеприведенных формулах (5.4) – (5.7) число n=10 (см. также Лекцию 3). Затем возьмем вторую выборку из 20 КР и вычислим на их основе среднее Хср20, стандартное отклонение S20, смещение В20 и полную ошибку ТЕ20, положив в формулах (5.4) – (5.7) число n=20. И, наконец, возьмем третью выборку из всех 30 КР и вычислим для них среднее Хср30, стандартное отклонение S30, смещение В30, и полную ошибку ТЕ30 , положив в формулах (5.4) – (5.7) число n=30.
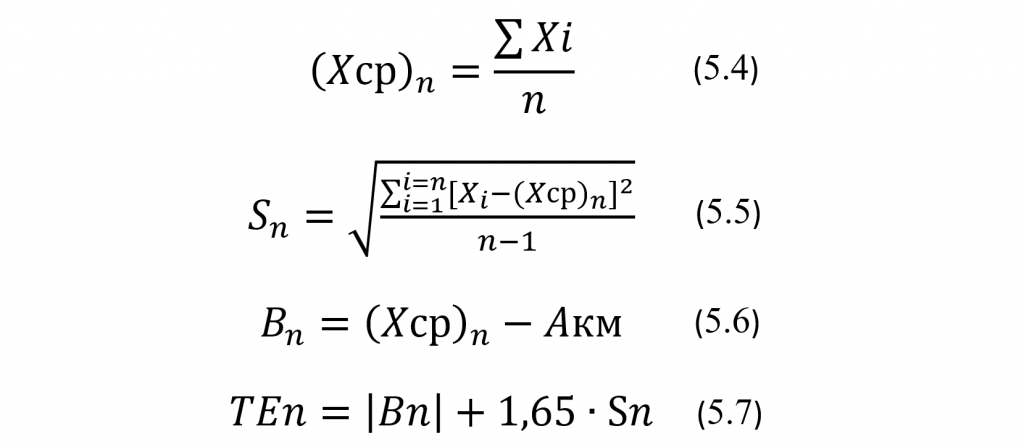
где Акм — аттестованное (паспортное) значение уровня аналита в используемом контрольном материале. Как видно из формулы (5.6) показатель Bn, в отличие от показателя Sn, может иметь и положительные и отрицательные значения. Напомним, что полная ошибка АС характеризует при заданном уровне достоверности максимальное отклонение результатов измерения уровня аналита от его фактического значения в исследуемой биопробе.
Для простоты предположим, что проверка выборок их этих соответственно 10, 20 и 30 КР показала отсутствие среди них выбросов, то есть, что среди них не оказалось ни одного результата, который отклонился бы от своего среднего более, чем на три соответственно S10, S20 и S30. Это предположение позволяет не пересчитывать заново оценочные значения АХ для исследуемой АС, как это обычно необходимо делать после исключения выбросов из выборки. Таким образом будем считать полученные оценки эксплуатационных значений АХ АС окончательными. Далее, используя нужное число результатов n (n=10, 20 и 30) и полученные оценочные значения Хср10, S10,В10, Хср20, S20, В20 , Хср30, S30 и В30, вычислим по формулам (5.8) – (5.15) нижнюю и верхнюю границы 95% доверительных интервалов соответственно для генеральных значений среднего µ, стандартного отклонения σ, систематического смещения ∆ = µ-Акм и полной ошибки τ. Для определения соответствующих значений для квантилей tα/2,n-1 распределения Стьюдента и квантилей χ2(1-α)/2,n-1 и χ2(1-α)/2,n-1 распределения Пирсона (распределения χ2) будем использовать известные табличные данные для этих распределений (см. Таблицы 5.1 и 5.2).
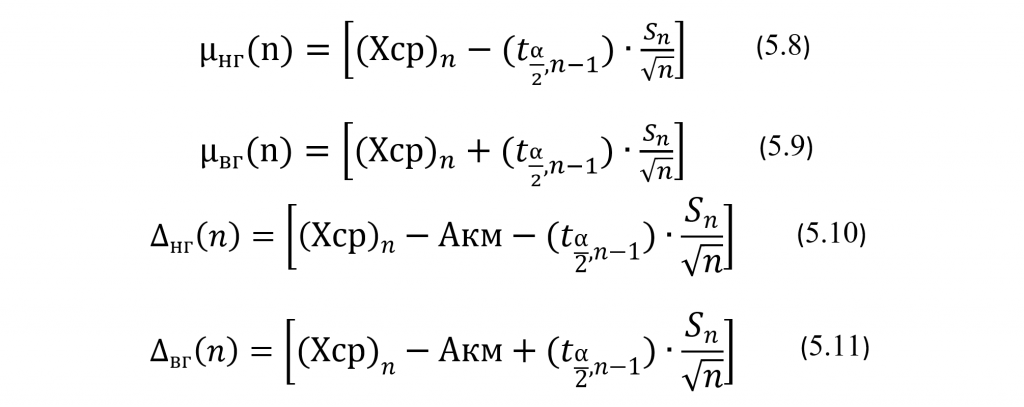
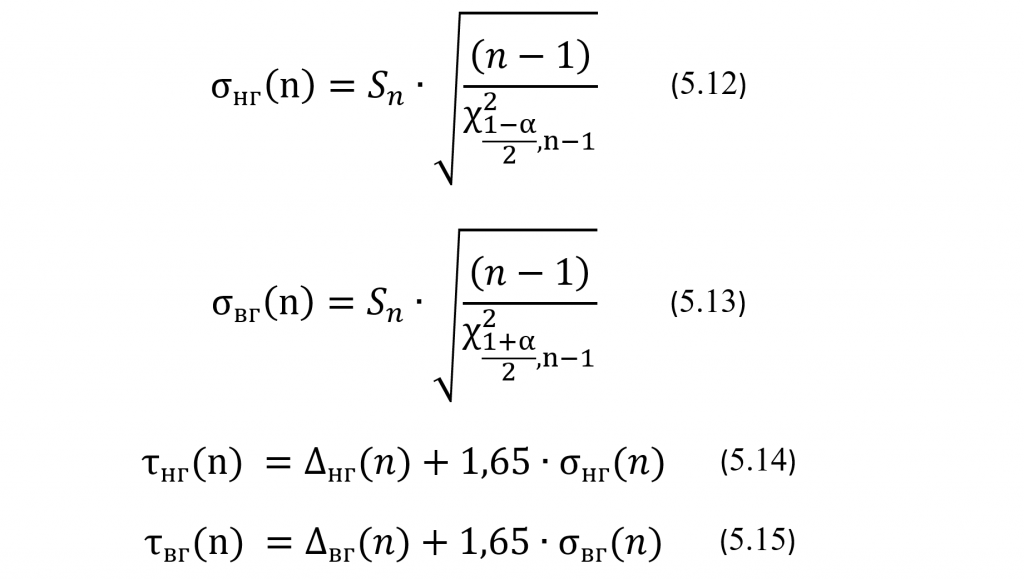
Таблица 5.1. Таблица квантилей tα/2,n-1 распределения Стьюдента для случая двусторонней гипотезы
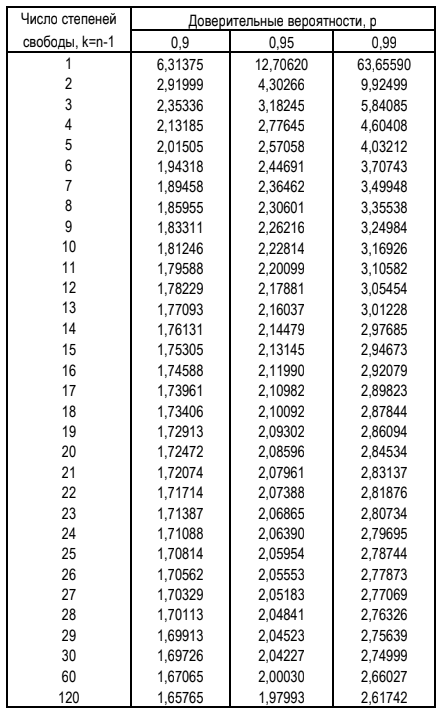
Таблица 5.2. Таблица квантилей (критических значений) распределения Пирсона (χ2)
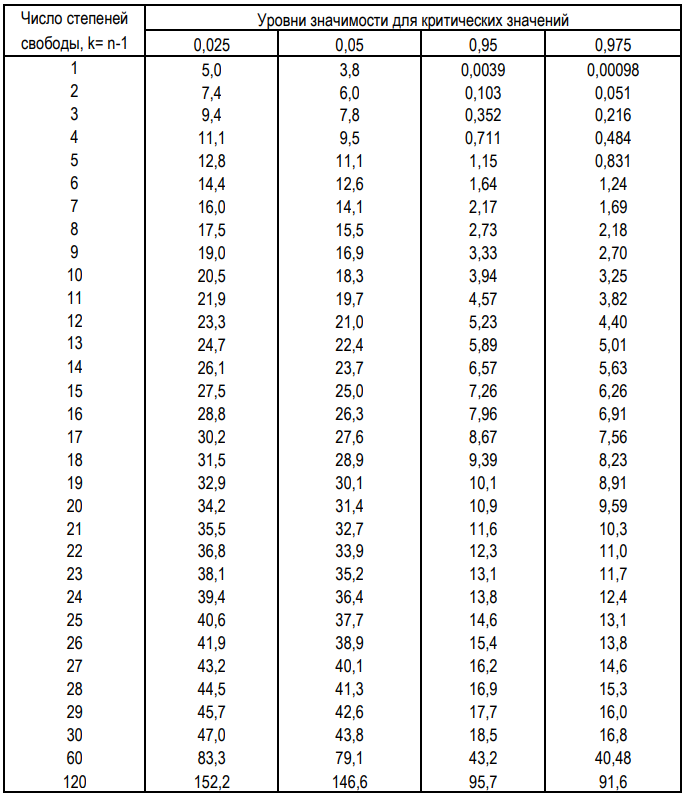
И, наконец, по нижеприведенным формулам (5.16) – (5.18) вычислим оценочные значения для относительного систематического смешения Вn,%, межсерийного коэффициента вариации CVn и относительной полной ошибки TEn,% в процентах от Хсрn, а затем на их основе вычислим по формулам (5.19) – (5.24) границы 95% доверительных интервалов для их генеральных значений, также в процентах от Хсрn.
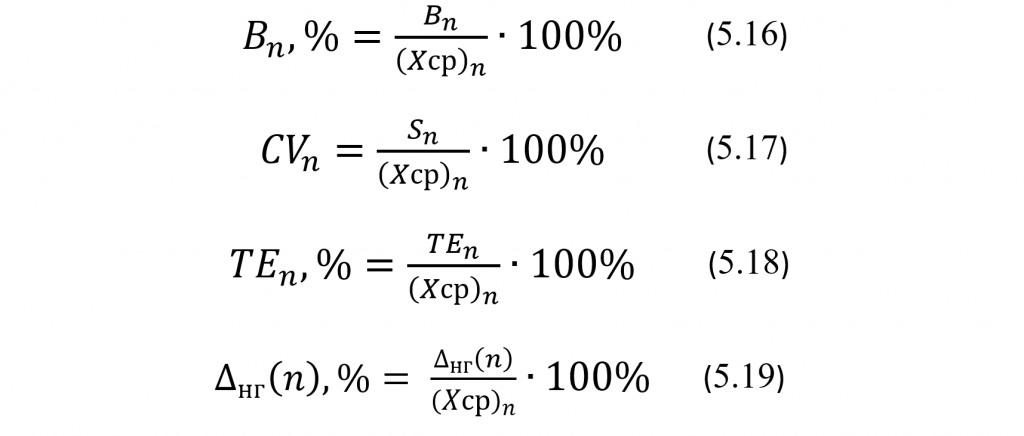
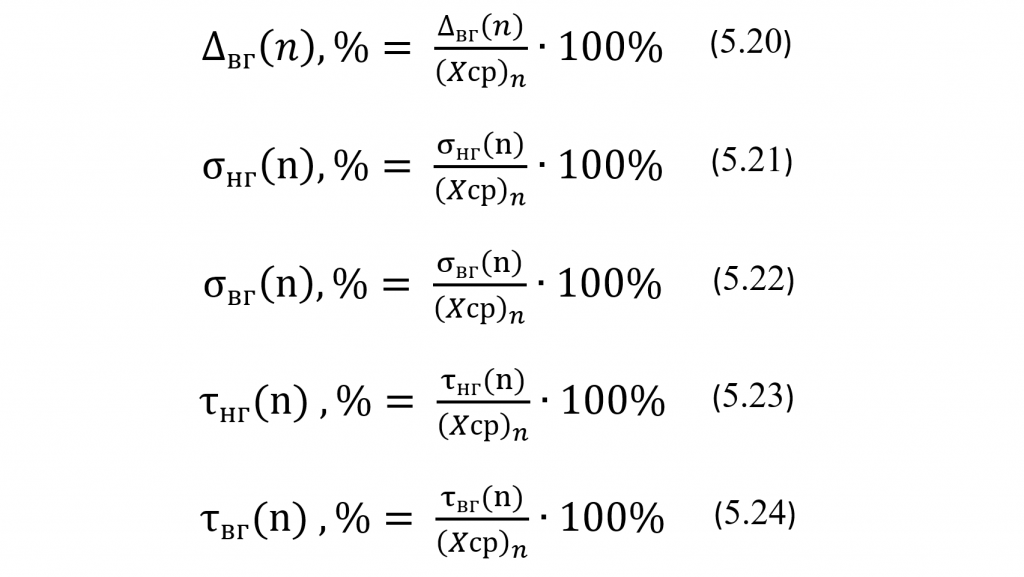
И, наконец, используя формулы и таблицы, приведенные выше в этой лекции, вычислим для выборок из 10, 20 и 30 КР границы 95% доверительных интервалов для генеральных значений относительного систематического смещения ∆,%, коэффициента вариации σ,% и относительной полной ошибки τ,%.
Для первой выборки эти границы будут вычисляться по следующим формулам:
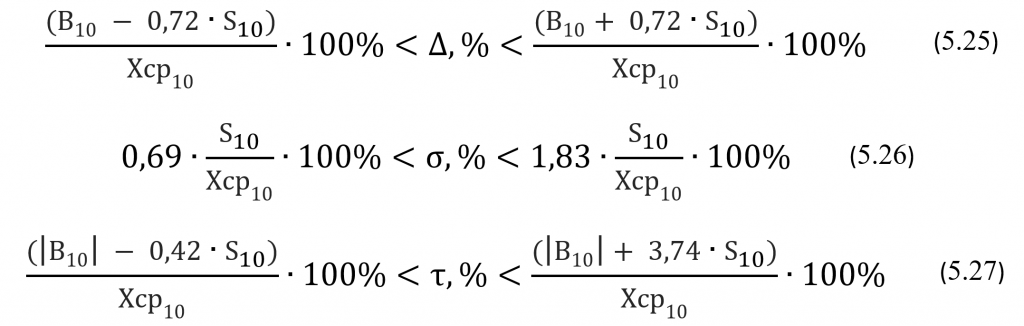
В формуле (5.25) величина ∆нг(10),% = [(B10 — 0,72*S10) / Хср10]*100% является нижней границей, а величина ∆вг(10),% = [(B10 + 0,72*S10) / Хср10]*100% является верхней границей 95% доверительного интервала для генерального значения относительного систематического смещения ∆,%. Соответственно в формуле (5.26) величина σнг(10),% = 0,69*(S10 / Хср10)*100% является нижней границей, а величина σвг(10),% = 1,83*(S10 / Хср10)*100% является верхней границей 95% доверительного интервала для генерального значения коэффициента вариации σ,%. И, наконец, в формуле (5.27) величинаτнг(10),% = [(|B10|- 0,42*S10) / Хср10]*100% является нижней границей, а величина τвг(10),% = [(|B10|+ 3,74*S10) / Хср10]*100% является верхней границей 95% доверительного интервала для генерального значения относительной полной ошибки τ,%.
Алгоритм проверки соответствия установленным нормам эксплуатационных значений перечисленных выше АХ следующий:
а) если вычисленные верхние границы ∆вг(10),%, σвг(10),% и τвг(10),% 95% доверительных интервалов для генеральных значений соответственно относительного систематического смещения ∆,%, коэффициента вариации σ,% и относительной полной ошибки τ,% не будут превышать установленных для них предельных значений, указанных в формулах (5.1) – (5.3), то тогда с 95% надежностью можно утверждать, что эксплуатационные значения относительного систематического смещения, коэффициента вариации и относительной ошибки данной АС удовлетворяют установленным для них нормам;
б) если вычисленные нижние границы ∆нг(10),%, σнг(10),% и τнг(10),% 95% доверительных интервалов для генеральных значений соответственно относительного систематического смещения ∆,%, коэффициента вариации σ,% и относительной полной ошибки τ,% будут превышать установленных для них предельных значений, указанных в формулах (5.1) – (5.3), то тогда с 95% надежностью можно утверждать, что эксплуатационные значения относительного систематического смещения, коэффициента вариации и относительной ошибки данной АС не удовлетворяют установленным для них нормам;
в) если вычисленные на основе выборки из 10 КР верхние границы соответствующих доверительных интервалов для генеральных значений основных АХ и/или полученные оценочные значения В10,%, CV10 и ТЕ10,% будут превышать установленные для них предельные значения, указанные в формулах (5.1) – (5.3), а нижние границы соответствующих доверительных интервалов для их генеральных значений не будут превышать этих предельных значений, то тогда следует увеличить объем выборки контрольных результатов до 20 или даже до 30.
Для второй выборки объемом 20 КР границы 95% доверительных интервалов для генеральных значений относительного систематического смещения ∆,%, коэффициента вариации σ,% и относительной полной ошибки τ,% будут вычисляться по следующим формулам:
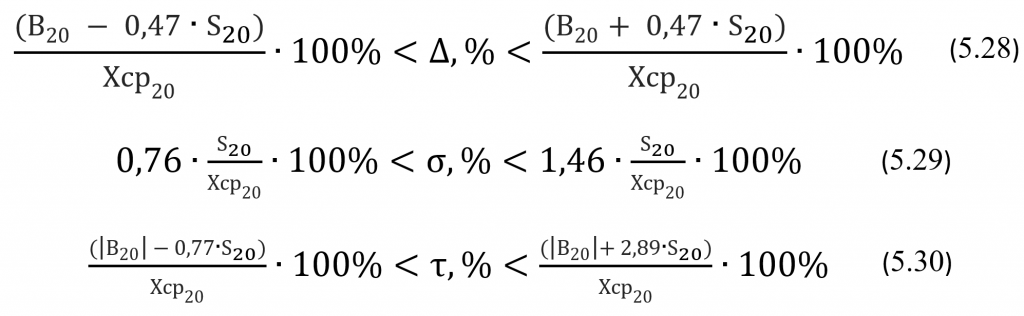
В формуле (5.28) величина ∆нг(20),% = [(B20 — 0,47*S20) / Хср20]*100% является нижней границей, а величина ∆вг(20),% = [(B20 + 0,47*S20) / Хср20]*100% является верхней границей 95% доверительного интервала для генерального значения относительного систематического смещения ∆,%. Соответственно в формуле (5.29) величина σнг(20),% = 0,76*(S20 / Хср20)*100% является нижней границей, а σвг(20),% = 1,46*(S20 / Хср20)*100% является верхней границей 95% доверительного интервала для генерального значения коэффициента вариации σ,%. И, наконец, в формуле (5.30) величина τнг(20),% = [(|B20| — 0,77*S20) / Хср20]*100% является нижней границей, а величина τвг(20),% = [(|B20| + 2,89*S20) / Хср20]*100% является верхней границей 95% доверительного интервала для генерального значения относительной полной ошибки τ,%.
Алгоритм проверки соответствия установленным нормам эксплуатационных значений перечисленных выше АХ, рассчитанных по выборке из 20 КР, такой же как и ранее описанный для АХ, вычисленных по выборке из 10 КР.
Для третьей выборки объемом в 30 КР границы 95% доверительных интервалов для генеральных значений относительного систематического смещения ∆,%, коэффициента вариации σ,% и относительной полной ошибки τ,% будут вычисляться по следующим формулам:

В формуле (5.31) величина ∆нг(30),% = [(B30 — 0,37*S30) / Хср30]*100% является нижней границей, а величина ∆вг(30),% = [(B30 + 0,37*S30)/Хср30]*100% является верхней границей 95% доверительного интервала для генерального значения относительного систематического смещения ∆,%. Соответственно в формуле (5.32) величина σнг(30),% = 0,80*(S30 / Хср30)*100% является нижней границей, а σвг(30),% = 1,35*(S30 / Хср30)*100% является верхней границей 95% доверительного интервала для генерального значения коэффициента вариации σ,%. И, наконец, в формуле (5.33) величина τнг(30),% = [(|B30|- 0,95*S30) / Хср30]*100% является нижней границей, а величина τвг(30),% = [(|B30| + 2,60*S30) / Хср30]*100% является верхней границей 95% доверительного интервала для генерального значения относительной полной ошибки τ,%.
Алгоритм проверки соответствия установленным нормам эксплуатационных значений перечисленных выше АХ, рассчитанных по выборке из 30 КР, такой же как и ранее описанный для АХ, вычисленных по выборке из 10 контрольных результатов.
Если и в этом случае полученные оценочные значения В30,%, CV30 и ТЕ30,% будут превышать установленные для них предельные значения, указанные в формулах (5.1) – (5.3), а нижние границы соответствующих доверительных интервалов для их генеральных значений не будут превышать этих предельных значений, то тогда действительно следует начать работы по выявлению источников запредельно большой составляющей или составляющих ошибки АС и провести работу по ее или их устранению. Если такие источники выявить не удастся, то всегда остается возможность улучшить прецизионность АС за счет увеличения кратности измерений уровня аналита в биопробе и/или ее правильность путем коррекции величины смещения.
В заключение лекции приведем для каждой из трех выборок примеры сравнения с установленными нормами АХ абстрактной АС для определения содержания глюкозы в сыворотке. Как было упомянуто выше ПДЗ АХ АС для определения содержания глюкозы в сыворотке, вычисленные на основе биологических вариаций по формулам (5.1) – (5.3), будут иметь следующие значения: Ва,% = ±2,34%, CVa = 2,80% и соответственно ТЕа,% = 6,96%. Предположим, хотя в действительности этого никогда не бывает, что для этой абстрактной АС заранее известны генеральные значения ее АХ, а именно: ∆,% = 1,90%, σ,% =1,90% и соответственно τ,% = 5,04%. То есть теоретически эксплуатационные значения АХ этой абстрактной АС соответствуют установленным нормам, причем даже с некоторым запасом.
Предположим теперь, что для выборки из 10 КР были получены следующие оценочные значения для АХ абстрактной АС: В10,% = +2,70%, CV10 = 3,50% и соответственно ТЕ10,%= 8,48%. Используя формулы (5.16) – (5.18) и (5.25) – (5.27) вычислим границы 95% доверительных интервалов для генеральных значений АХ с учетом объема выборки, равного 10 КР. В результате получим:
0,18% < ∆,% < 5,22%
2,42% < σ,% < 6,41%
1,23% < τ,% < 15,79%
Из этих данных, полученных для выборки из 10 КР, следует, что нижние границы соответствующих 95% доверительных интервалов для их генеральных значений не превышают установленные для них предельные значения, а оценочные значения В10,%, CV10 и ТЕ10,% и верхние границы соответствующих доверительных интервалов для их генеральных значений превышают эти предельные значения, причем существенно. Из пункта в) алгоритма сравнения АХ АС с нормами, изложенного в конце данной лекции, следует, что надо увеличить объем выборки контрольных результатов до 20 или даже до 30.
Теперь предположим, что для выборки из 20 КР были получены следующие оценочные значения для АХ абстрактной АС: В20,% = +2,2%, CV20 = 2,5% и соответственно ТЕ20,% = 6,33%. Используя формулы (5.16) – (5.18) и (5.28) – (5.30) вычислим границы 95% доверительных интервалов для генеральных значений АХ с учетом объема выборки, равного 20 КР. В результате получим:
1,03% < ∆,% < 3,38%
1,90% < σ,% < 3,65%
0,28% < τ,% < 9,43%
Из этих данных, полученных для выборки из 20 КР, следует, что оценочные значения В20,%, CV20 и ТЕ20,% и нижние границы соответствующих 95% доверительных интервалов для их генеральных значений не превышают установленные для них предельные значения, а верхние границы соответствующих доверительных интервалов для их генеральных значений превышают эти предельные значения, хотя не столь существенно как в случае с выборкой из 10 КР. Из пункта в) алгоритма сравнения АХ АС с нормами, изложенного в конце данной лекции, следует, что разумно увеличить объем выборки контрольных результатов до 30.
Теперь предположим, что для выборки из 30 КР были получены следующие оценочные значения для АХ абстрактной АС: В30,% = +1,91%, CV30 = 1,94% и соответственно ТЕ30,% = 5,11%. Используя формулы (5.16) – (5.18) и (5.31) – (5.33) вычислим границы 95% доверительных интервалов для генеральных значений АХ с учетом объема выборки, равного 30 КР. В результате получим:
1,19% < ∆,% < 2,63%
1,55% < σ,% < 2,62%
0,07% < τ,% < 6,95%
Из этих данных, полученных для выборки из 30 КР, следует, что верхние границы соответствующих 95% доверительных интервалов для генеральных значений АХ абстрактной АС не превышают установленные для них предельные значения. Тогда из пункта а) алгоритма сравнения АХ АС с нормами, изложенного в конце данной лекции, следует, что с 95% надежностью можно утверждать, что эксплуатационные значения относительного систематического смещения, коэффициента вариации и относительной ошибки данной АС удовлетворяют установленным для них нормам.
Краткие выводы по Лекции 5.
- Для принятия решения о возможности запуска в эксплуатацию новой или обновленной аналитической системы прежде всего необходимо убедиться, что ее аналитические характеристики соответствуют установленным нормам.
- В качестве норм в настоящее время принято использовать предельно допускаемые значения основных аналитических характеристик, вычисляемые на основе внутри- и межиндивидуальных коэффициентов биологических вариаций уровней аналитов in vivo.
- Критерий соответствия аналитических характеристик аналитической системы нормам заключается в следующем: генеральные эксплуатационные значения ее основных аналитических характеристик не должны превышать установленных для них предельно допускаемых значений.
- При отсутствии данных о генеральных эксплуатационных значениях основных аналитических характеристик для проверки их соответствия нормам следует использовать нижние и верхние границы доверительных интервалов для генеральных значений, вычисляемые по их выборочным оценкам.
- Алгоритм проверки соответствия установленным нормам эксплуатационных значений основных аналитических характеристик на основе использования границ доверительных интервалов для их генеральных значений следующий:
а) если вычисленные верхние границы 95% доверительных интервалов для генеральных значений соответственно относительного систематического смещения, коэффициента вариации и относительной полной ошибки не будут превышать установленных для них предельных значений, то тогда с 95% надежностью можно утверждать, что эксплуатационные значения относительного систематического смещения, коэффициента вариации и относительной ошибки удовлетворяют установленным для них нормам;
б) если вычисленные нижние границы 95% доверительных интервалов для генеральных значений соответственно относительного систематического смещения, коэффициента вариации и относительной полной ошибки будут превышать установленные для них предельные значения, то тогда с 95% надежностью можно утверждать, что эксплуатационные значения относительного систематического смещения, коэффициента вариации и относительной ошибки данной АС не удовлетворяют установленным для них нормам;
в) если вычисленные верхние границы соответствующих доверительных интервалов для генеральных значений и/или полученные оценочные значения для относительного систематического смещения, коэффициента вариации и относительной полной ошибки будут превышать установленные для них предельные значения, а нижние границы соответствующих доверительных интервалов для их генеральных значений не будут превышать эти предельные значения, то тогда следует увеличить объем выборки контрольных результатов.
Литература к Лекции 5.
1. https://www.westgard.com/biodatabase1.htm
2. ГОСТ Р 53133.1-2008. Национальный стандарт РФ. «Технологии лабораторные клинические. Контроль качества клинических лабораторных исследований.» Часть 1. «Пределы допускаемых погрешностей результатов измерения аналитов в клинико-диагностических лабораториях».
3. ГОСТ Р 53133.2-2008. Национальный стандарт РФ. «Технологии лабораторные клинические. Контроль качества клинических лабораторных исследований.» Часть 2. «Правила проведения внутрилабораторного контроля качества количественных методов клинических лабораторных исследований с использованием контрольных материалов».


