Лекция 3. Технологии определения аналитических характеристик аналитических систем

М.И.Прищепа, кандидат технических наук, ЗАО «Аналитика»

В настоящей лекции будут описаны процедуры общепринятых технологий определения на практике эксплуатационных значений основных аналитических характеристик аналитических систем, а также рассмотрены вопросы точности определения этих значений.

Основными аналитическими характеристиками аналитических систем (далее – АС), как было сказано в Лекции 2, являются систематическое смещение ∆ и стандартное отклонение σ, которые также называют систематической и случайной составляющей погрешности АС. Эти две составляющие при заданном уровне доверия сполна определяют максимальную величину полной погрешности ТЕас результатов измерений содержания аналита в биопробах, получаемых с использованием данной АС.

Очень важно помнить, что один и тот же экземпляр АС, эксплуатируемый в разных внешних условиях температуры, влажности, чистоты воздуха, электропитания, электромагнитной близости другого оборудования и т.д. и т.п., будет обладать скорее всего разными эксплуатационными значениями аналитических характеристик. Иногда даже перемещение АС из одного помещения в другое значительно изменяет эти значения.

Итак, примем к сведению, что каждая АС обычно обладает уникальными значениями аналитических характеристик, характерными для конкретных условий ее эксплуатации и диапазона измерений. Теоретически оценивать эти характеристики можно двумя методами.

При использовании первого метода исходят из возможности оценивать значения аналитической характеристики АС путем суммирования определенным образом индивидуальных значений этой характеристики каждого из измерительных преобразователей (далее – ИП), входящих в состав этой АС. Иными словами, путем учета взноса аналитических характеристик отдельных ИП в составе АС в итоговое значение той или иной составляющей ее погрешности. Понятно, что для этого надо потребовать от изготовителя каждого ИП предоставлять в документации соответствующую информацию о его аналитических характеристиках при тех или иных условиях его эксплуатации. Хотя понятно, что даже если такая информация и будет представлена в документации, нет никаких гарантий, что она будет верна для конкретных условий эксплуатации ИП. Да и оценивать по ней итоговое значение каждой составляющей погрешности будет все равно достаточно непросто для сотрудников лабораторий. Заметим, что этот метод – по крайней мере в части определения систематического смещения АС – является вариантом  практической реализации рекомендаций соблюдения лабораториями условий прослеживаемости измерений [1], упомянутых в начале Лекции 1, требующих оценки итоговой величины неопределенности результатов при передаче размера единицы физической величины от ее эталона к калибруемому средству измерений.

В связи со сложностью практической реализации первого метода для достижения той же цели обычно лаборатории используют так называемый метод «чёрного ящика» и определяют аналитические характеристики АС сразу же как цельного средства измерения, то есть без детализации на ИП, входящих в состав АС. Термин «чёрный ящик» используют для обозначения системы, внутреннее устройство и механизм работы которой или очень сложны, или неизвестны или просто неважны в рамках решаемой задачи. Метод «чёрного ящика» — метод исследования таких систем, когда вместо свойств и взаимосвязей составных частей системы изучается ее реакция как целого на тот или ной вид воздействия, на нее направленный.

В теории измерений обычно метод «черного ящика» используют для описания работы преобразователя сигналов, поступающих на его вход, когда нет необходимости знать о его содержимом в деталях. Аналитические характеристики таких черных ящиков определяют путем сравнения формы и структуры измерительных сигналов, входящих в него и выходящих из него. Любая АС для лабораторий это и есть, по сути, тот самый «черный ящик». На вход такого «черного ящика», то есть АС, подают образец пробы пациента или образец контрольного материала (далее — КМ) или образец калибратора как есть или преобразованный, а на выходе этого «черного ящика» имеют измерительную информацию, характеризующую уровень аналита в исследуемом образце, поданном на его вход. Чтобы узнать, насколько такая измерительная информация может быть далека от фактического уровня аналита в исследуемом образце, совсем не обязательно разбираться в конструкции и механизме работы «черного ящика» и выяснять насколько аналитически точно он на каждом отдельном шаге измерительного процесса преобразовывает одну физическую величину в другую, пытаясь таким образом обеспечивать прослеживаемость результатов проводимых измерений. Чтобы определить аналитические характеристики «черного ящика», то есть АС в целом, вполне достаточно подавать на вход «черного ящика» в течение определенного времени серии аликвот эталона состава или свойств биопробы с заранее известным содержанием искомого аналита. А затем сравнить полученные на выходе «черного ящика» результаты измерения между собой и с заранее известным уровнем аналита в образце на его входе. Конечно и тут не все так просто.

Если для каких-либо аналитов нет таких эталонов, а их пока нет для очень многих аналитов, то тогда вместо эталонов можно использовать или эрзац-эталоны в виде контрольных материалов (далее – КМ) промышленного изготовления, близких по матрице к пробам пациентов, или неаттестованные, но застабилизированные по составу пробы пациентов. В последнем случае, по понятным причинам, требуется наличие также референтных методов измерения уровней искомых аналитов, чтобы иметь возможность аттестовать содержание аналита в используемой биопробе. На практике применяют и другие технологии замены эталонов состава и свойств, позволяющие лаборатории оценивать правильность определения содержания аналита в образцах КМ или в пробах пациентов. Эти технологии основаны либо на участии лаборатории с исследуемой АС в программе ВОК, либо на ведении для нее контроля качества по ежедневным средних по пациентам.

Далее в этой лекции мы будем рассматривать использование только второго метода для определения истинных эксплуатационных значений аналитических характеристик АС, то есть как цельного средства измерений. При этом будем иметь ввиду, что истинные эксплуатационные значения этих характеристик можно определить только теоретически путём проведения очень большого количества повторных измерений уровня аналита в аликвотах одного и того же эталона или одной и тоже биопробы, что по понятным причинам реализовать достаточно сложно, вернее сказать, что это по разным объективным причинам в принципе на практике невозможно.

На практике делают только так называемые выборочные оценки этих истинных значений, проводя ограниченное, но статистически значимое количество повторных измерений уровня аналита в аликвотах одного и того же биоматериала, для чего обычно используют контрольный материал промышленного изготовления с аттестованным содержанием искомого аналита.

У выборочных оценок с ограниченным объемом измерений есть как плюсы, так и минусы по сравнению с чрезмерно большой выборкой. Основной плюс заключается в том, что для проведения первых требуется гораздо меньше ресурсов, чем для проведения вторых. Основной минус состоит в том, что выборочные оценки всегда имеют какие-то отклонения от истинных значений. Более того, повторные выборочные оценки практически всегда отличаются друг от друга. Поэтому основная задача проведения выборочных оценок заключается в получении нужной для них точности при минимизации временных и материальных затратах на их проведение.

Правила получения выборочных оценок истинных значений систематического смещения и стандартного отклонения АС в условиях ее эксплуатации, которые будем обозначать соответственно В_n и S_n для выборок объемом n, стандартизованы и описаны в приказе Минздрава РФ № 220 [2] и в ГОСТ Р 53133.2-2008 [3]. Помимо отечественных руководящих документов рекомендации по проведению оценки эксплуатационных значений аналитических характеристик АС изложены в зарубежных стандартах, например, в руководстве EP15-A3 [4] Clinical and Laboratory Standards Institute, который является одним из ведущих международных организаций в области стандартизации. Хотя процедуры проведения такой оценки, описанные в этих документах, несколько и отличаются друг о друга, но не принципиально.

Отечественные и международные правила исходят из того, что необходимо определять основные аналитические характеристики для всех АС, которые планируется вводить в эксплуатацию, в том числе и для АС, основные части которых подвергались или ремонту, или замене. А затем сравнить их с установленными нормами, чтобы принять решение о запуске новой или обновленной АС в эксплуатацию.

Аналитические характеристики АС в пределах желаемого диапазона измерений определяют путем статистической обработки результатов повторных (или что тоже самое – многократных) измерений содержания аналита в аликвотах нескольких биоматериалов с разными уровнями искомого аналита, более или менее равномерно распложенными внутри этого диапазона. Последнее связано с тем, что эксплуатационные значения аналитических характеристик, как правило, зависят не только от условий эксплуатации АС, но и от уровня аналита в биопробе. Из теории измерений известно, что генеральная, то есть бесконечно большая совокупность результатов повторных измерений на одной и той же АС уровня аналита в аликвотах одного и того же биоматериала будут распределены по нормальному закону со своими конкретными значениями параметров распределения — математического ожидания µ и стандартного отклонения σ. Практика же показывает, что достаточно большая совокупность или, как говорят, представительная выборка повторных измерений может при определенных условиях достаточно хорошо описывать их распределение и в генеральной совокупности, позволяя только с помощью выборочных результатов достаточно точно оценивать значения показателей распределения µ и σ. Одно из этих условий состоит в отсутствии среди результатов в выборке так называемых выбросов. Для накопления нужного количества n результатов повторных измерений, или, как говорят, представительной выборки объемом n, адекватно характеризующей их распределение в генеральной совокупности, что необходимо для достаточно надежной оценки истинных значений систематического смещения и стандартного отклонения, на АС проводят так называемые установочные серии. Чтобы получить представление о поведении аналитических характеристик в пределах диапазона измерений АС, рекомендуют проводить установочные серии с использованием хотя бы двух биоматериалов с двумя разными уровнями аналита, характерных для принятия клинических решений. Поэтому при проведении установочных серий необходимо использовать минимум два биоматериала с уровнями исследуемого аналита, характерными для нормы и патологии.

Из положений математической статистики следует, что для того, чтобы выборка результатов повторных измерений объемом n была представительной, а полученные выборочные значения аналитических характеристик являлись надежными оценками их истинных значений, число n должно быть не менее 20. Поэтому в отечественных правилах [2, 3] число n выбрано равным 20, а в документе CLSI — равным 25, вернее не менее, чем 25. Отличие процедур, описываемых в этих документах, состоит также в том, что в соответствии с отечественными правилами, установочную серию проводят в течение 20 рабочих дней, проводя по одному измерению ежедневно в каждом из двух типов КМ, а по документу CLSI установочную серию рекомендовано проводить или в течение 5 рабочих дней по 5 повторных измерений в одной аналитической серии ежедневно или в течение 7 рабочих дней по 4 повторных измерения в одной аналитической серии ежедневно.

Необходимость накопления экспериментальных данных для проведения оценки эксплуатационных значений аналитических характеристик в течение такого длительного срока связана с тем, что воспроизводимость результатов повторных измерений в течение кратких сроков эксплуатации АС всегда значительно лучше по сравнению с воспроизводимостью в течение длительных сроков ее эксплуатации. Краткосрочная воспроизводимость, то есть воспроизводимость в пределах одной аналитической серии или в пределах рабочего дня называется повторяемостью, а долгосрочная воспроизводимость, то есть воспроизводимость изо дня в день – прецизионностью. Очевидно, что данные, полученные в установочной серии в течение большего количества рабочих дней, будут более адекватно характеризовать воспроизводимость результатов изо дня в день, то есть прецизионность АС. Следует отметить, что для решения клинических задач именно этот показатель является наиболее важным.

Используя все n результатов повторных измерений, полученных в установочной серии, вычисляют по нижеприведенным формулам их среднеарифметическое значение (Хср)_n, которое является, как говорят, выборочной оценкой истинного или, что тоже самое, генерального значения математического ожидания µ, и стандартное отклонение S_n, которое является, как говорят, выборочной оценкой истинного или, что тоже самое, генерального значения σ.

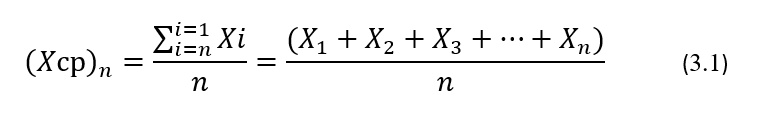
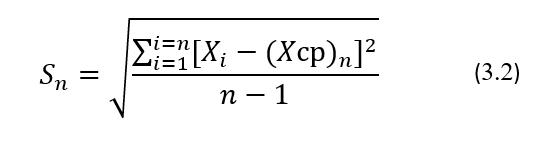
Выборочные оценки генерального значения σ, вычисленные по формуле (3.2), являются несмещенными оценками стандартного отклонения. Следует иметь ввиду, что оценки этого статистического показателя, рассчитываемые по формуле

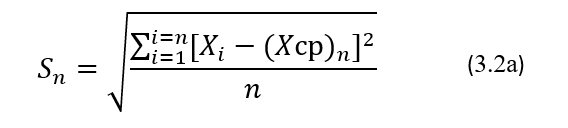
вытекающей из определения дисперсии, при малых объемах выборки являются смещенными и всегда менее точно характеризуют его генеральное значение. Поэтому при малых объемах выборки, когда n<100, этот показатель желательно оценивать так, чтобы его оценка была несмещенной, а именно по формуле (3.2). Обычно для расчетов несмещенных оценочных значений S_n используют формулу, аналогичную формуле (3.2), но преобразованную к виду, более удобному для проведения вычислений, а именно:

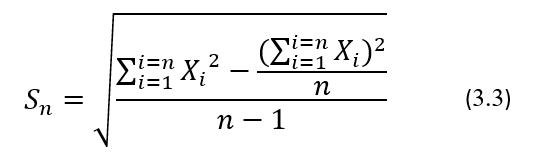
Как видно из вышеприведенных формул для вычисления значений S_n, они не могут быть отрицательными.

Таблица 3.1. Вычисление значений (Хср)n (формула 3.1) и Sn (формула 3.2) по результатам измерений уровня натрия в КМ с Акм = 144 ммоль/л.

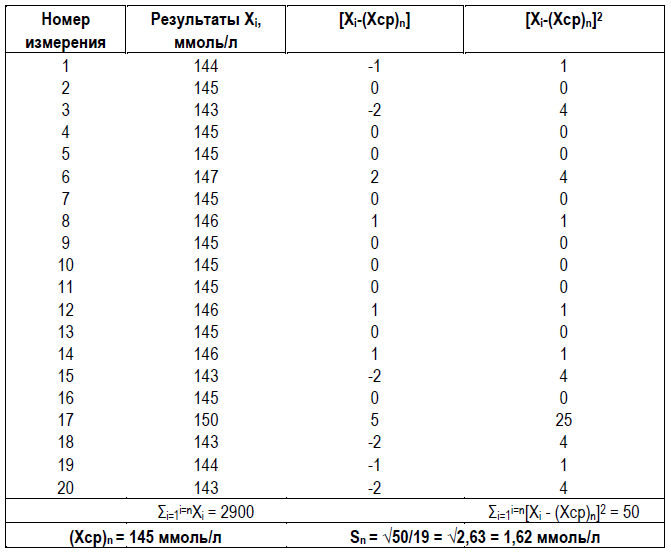
где X_i – i-тый результат (i=1,2,3,…,n) измерения; Σ_i=1ⁱ⁼ⁿX_i – сумма всех n результатов, начиная с X₁ и кончая X_n; (Xср)_n = Σ_i=1ⁱ⁼ⁿX_i/n = (X₁ +X₂ + X₃ +…+ X_n)/n – среднеарифметическое значение n результатов;

Σ_i=1ⁱ⁼ⁿ[X_i — (Xср)_n]² – сумма квадратов отклонений каждого из n результатов от их среднеарифметического значения; Σ_i=1ⁱ⁼ⁿX_i² – сумма квадратов результатов; (Σ_i=1ⁱ⁼ⁿX_i)² – квадрат суммы всех результатов измерений. Примеры вычислений (Xср)_n и S_n по вышеприведенным формулам представлены соответственно в Таблицах 3.1 и 3.2. Отличие вычислений в этих примерах состоит только в том, что в первом примере расчет значения S_n проводился по формуле (3.2), а во втором примере – по формуле (3.3). Как и следовало ожидать, значения S_n, вычисленные по формулам (3.2) и (3.3) совпадают.

Таблица 3.2. Вычисление значений (Хср)n (формула 3.1) и Sn (формула 3.3) по результатам измерений уровня натрия в КМ с Акм = 144 ммоль/л.

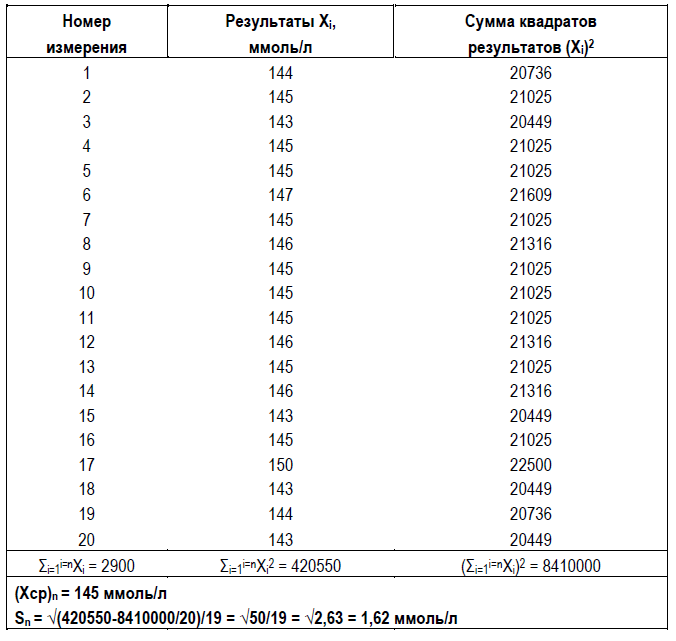
В руководстве [4] рекомендуется после вычисления значений (Xср)_n и S_n проверять все результаты установочной серии на наличие среди них результатов, сильно отклонившихся от выборочного среднего, то есть результатов, вышедших за границы определенных доверительных интервалов, близких к (Xср)_n ± 3*S_n и зависящих от выбранного уровня доверия. Такие результаты обычно принято называть грубыми ошибками или выбросами. При их наличии среди результатов, полученных в установочной серии, они изымаются из нее, а полученные ранее значения (Xср)_n и S_n рассчитывают заново, то есть без учета выбросов.

Из опыта известно, что результаты повторных измерений уровня аналита в одном и том же биоматериале, полученные с использованием АС с неизменными аналитическими характеристиками, всегда распределены по нормальному закону. При нормальном распределении результатов повторных измерений для выявления грубых ошибок (выбросов) обычно принято использовать статистический критерий Граббса [5].

В соответствии с положениями этого критерия сначала определяют среднее значение (Хср)_n и стандартное отклонение S_n, используя все результаты, полученные в установочной серии, затем выявляют среди них наименьший X_min и наибольший X_max результаты, предполагая, что они могут являться выбросами, затем, используя эти данные, рассчитывают критерий Граббса G₁ и G₂ соответственно для результатов Х_min и X_max по формулам:

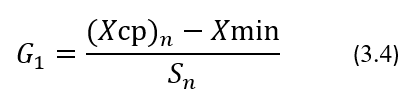
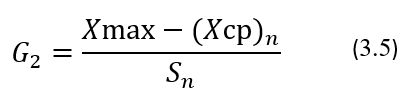
И, наконец, полученные расчетные значения G₁ и G₂ сравнивают с критическим значением G_T, приведённым в Таблице 3.3, которое соответствует количеству n результатов, полученных в установочной серии, и выбранному уровню доверия (уровню значимости). Если G₁ ≤ G_T, то результат X_min не считают грубой ошибкой и его сохраняют среди результатов установочной серии. Если G₂ ≤ G_T, то результат X_max не считают грубой ошибкой и его сохраняют среди результатов установочной серии. Если G₁ > G_T и/или G₂ > G_T, то тогда X_min и/или X_max считают грубыми ошибками и их исключают из результатов установочной серии как маловероятные значения.

Таблица 3.3. Критические значения G_T для критерия Граббса.

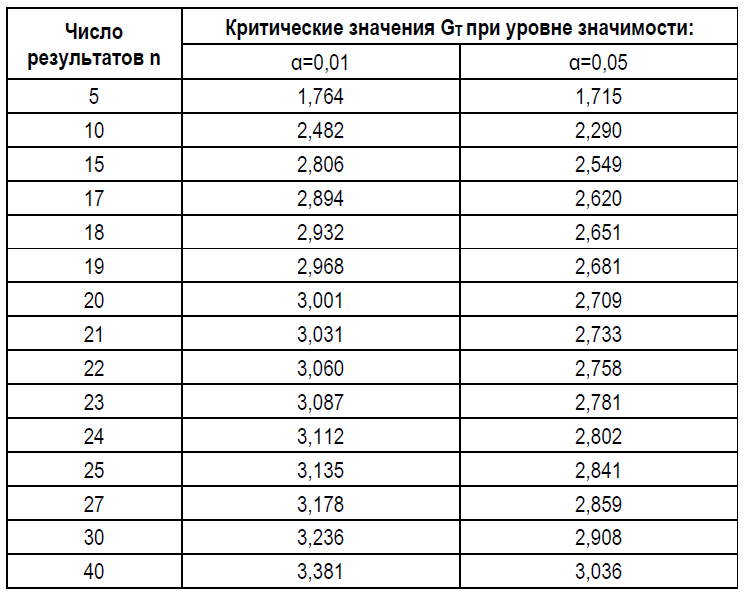
Таблица 3.4. Перерасчет значений (Хср)n (формула 3.1) и Sn (формула 3.2) после выявления по Граббсу грубой ошибки среди результатов, приведенных в Таблице 3.1.

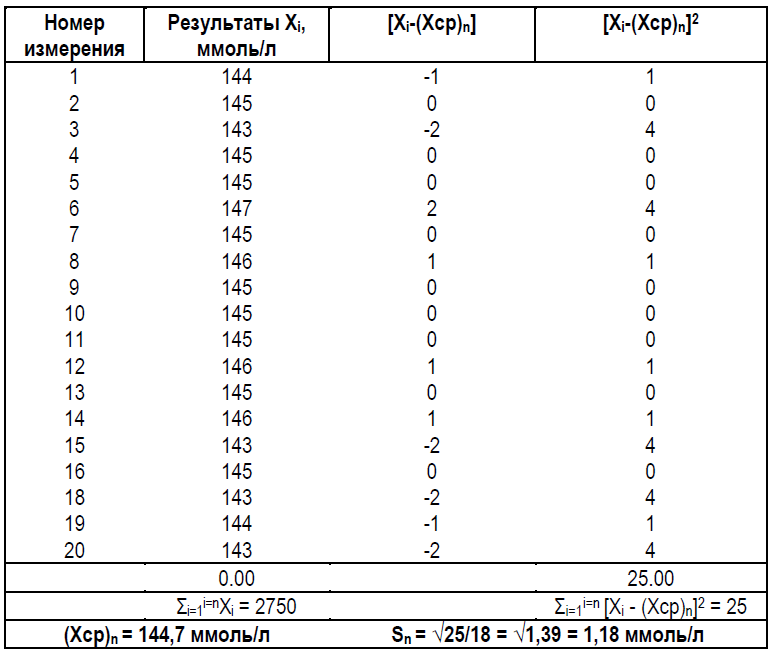
Далее, используя оставшиеся результаты, вычисляют для них среднеарифметическое значение и стандартное отклонение, после чего процедуру проверки наличия грубых ошибок среди оставшихся результатов повторяют заново. То есть, если среди 20 результатов повторных измерений применение критерия Граббса при выбранном 95% уровне доверия (что соответствует уровню значимости α=0,05) выявит грубую ошибку, показывая, что сомнительный результат отклонился от среднего в большую или меньшую сторону более, чем на 2,71*S_n, то тогда производят перерасчет среднеарифметического значения и стандартного отклонения по оставшимся 19 результатам. Далее приведен конкретный пример выявления грубой ошибки c 95% уровнем доверия (α = 0,05) среди 20 результатов измерений из Таблицы 3.1. Сначала по формулам (3.4) и (3.5) вычисляются значения G₁ и G₂: G₁ = (145-143) / 1,62 = 1,235 < G_T = 2,709 и соответственно G₂ = (150-145) / 1,62 = 3,09 > G_T = 2,709. Таким образом, по критерию Граббса среди результатов, приведенных в Таблице 3.1, имеется один выброс, а именно результат под номером 17, который изымается из последующего расчета (Хср)_n и S_n. Перерасчет значений (Хср)_n и S_n по формулам (3.1) и (3.2) приведен в Таблице 3.4. Заметим, что оценочное значение S_n стандартного отклонения, вычисленное сначала по 20 результатам измерений, которое мы обозначим как S_1, а затем после исключения грубой ошибки по 19 результатам измерений, которое мы обозначим как S₂, является и в том и в другом случае выборочной оценкой истинного значения стандартного отклонения генеральной совокупности результатов повторных измерений. Для проверки того, что и одно и другое выборочные значения S₁ и S₂ характеризуют одно и тоже истинное значение стандартного отклонения σ, точнее говоря, что эти оценочные значения не отличаются статистически значимо друг от друга, в математической статистике используют критерий Фишера, который также называют F-тестом [6]. В соответствии с этим критерием сначала вычисляют значение показателя F по формуле

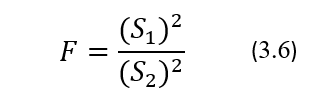
учитывая при этом, что S₁ > S₂ , а затем сравнивают его с табличным критическим значением Fкрит. Это критическое значение зависит от уровня значимости (уровня доверия) и от количества результатов n₁ и n₂, которые использовались для вычисления выборочных значений. При уровне доверия, равном 95%, S₁ = 1,62 ммоль/л, S₂ = 1,18 ммоль/л, n₁ = 20и n₂ = 19из таблиц критических значений для статистики Фишера находим, что Fкрит = 2,21. И поскольку для этого случая F = 2,62 / 1,39 = 1,89, что меньше Fкрит = 2,21, то согласно критерию Фишера полученные выборочные оценки истинного значения стандартного отклонения, равные соответственно 1,62 и 1,18 ммоль/л, статистически значимо друг от друга не отличаются.

Теперь проверим наличие грубой ошибки c 95% уровнем доверия (α=0,05) среди оставшихся 19 результатов измерений из Таблицы 3.4. По формулам (3.4) и (3.5) вычисляем значения G₁ и G₂: G₁ = (145-143) / 1,18 = 1,695 < G_T = 2,681 и соответственно G₂ = (147-145) / 1,18 = 1,695 < G_T = 2,681. Таким образом, по критерию Граббса среди оставшихся 19 результатов, приведенных в Таблице 3.4, грубых ошибок более нет.

Опыт эксплуатации показывает, что в среднем стабильность калибровки аналитических систем не превышает 48 часов, что может вызывать флуктуации или дрейф систематического смещения АС. Это, в свою очередь, может ухудшать прецизионность результатов повторных измерений уровня аналита в одном и том же биоматериале, в том числе и при проведении установочных серий. Чтобы выяснить насколько сильно ухудшается прецизионность АС из-за нестабильности ее калибровки можно использовать так называемый метод дупликатов, или иначе метод двойных измерений уровня аналита или в образцах КМ или непосредственно пробах пациентов. Суть метода состоит в том, что в течение n рабочих дней, где n ≥ 20, ежедневно в одной из аналитических серий измеряют уровень аналита в одном и том же биоматериале дважды, то есть в дупликатах, и затем вычисляют их разности d_i= X_1i – X_2i, где X_1i и X_2i – первый и второй результаты измерений, полученные в течение рабочего дня с порядковым номером i = 1,2,3,…,n. Вспомним, что из свойств математического ожидания и дисперсии  следует, что математическое ожидание µ_d разности d случайных величин X₁ и Х₂ равно разности их математических ожиданий µ_d = µ₁ — µ₂, а дисперсия σ_d² разности двух случайных независимых величин X₁ и Х₂ равна сумме их дисперсий σ_d² = σ₁² + σ₂². Воспользуемся этими свойствами и тогда получим для случайной величины d_i, что ее математическое ожидание µ_d равно нулю, поскольку µ₁ = µ₂, а ее дисперсия равна удвоенной дисперсии результатов измерений, поскольку σ₁² = σ₂² = σ². И тогда, соответственно, стандартные отклонения σ_d и σ будут связаны формулой: σ_d = √2*σ. Воспользуемся формулой (3.2а) для определения показателя σ и тогда получим формулу для вычисления оценочных значений стандартного отклонения S_n по разностям результатов, полученным методом двойных измерений:

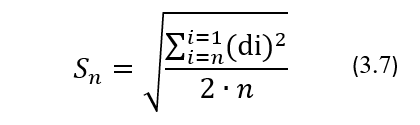
где d_i = X_1i – X_2i — разность между дупликатами, полученными в i-тый рабочий день, n – число биопроб, в которых уровень аналита был измерен в дупликатах. Следует иметь ввиду, что уровень аналита в используемых биопробах должен находиться в пределах диапазона измерений АС, в котором ее прецизионность, характеризуемая стандартным отклонением, практически не меняется. Конкретный пример вычисления для натрия значения S_n при измерении уровня аналита в дупликатах приведен в Таблице 3.5.

Таблица 3.5. Пример вычисления значения Sn по формуле (3.7)
методом двойных измерений уровня натрия в биопробах.

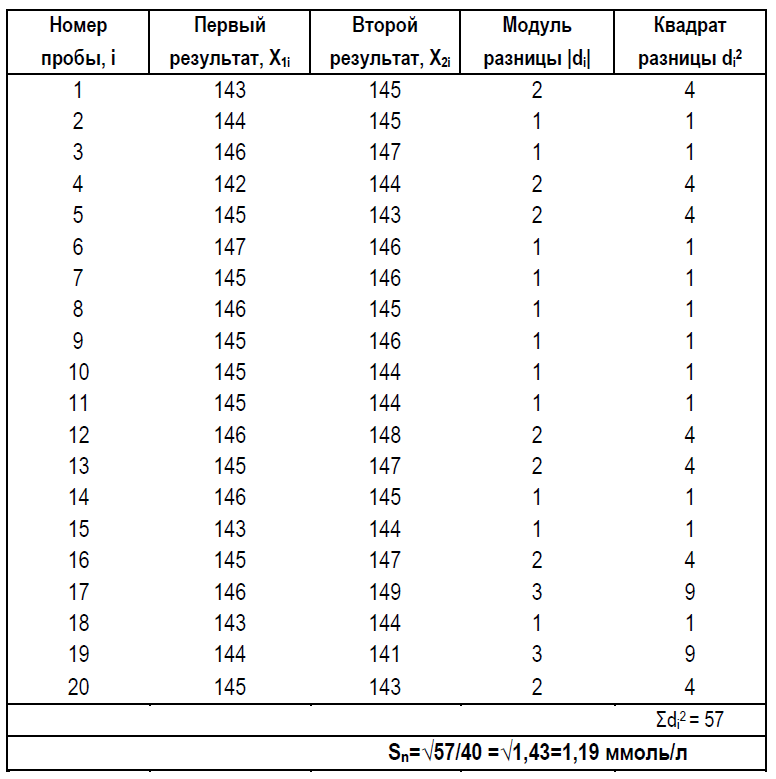
Теперь, используя критерий Фишера, проверим, отличаются статистически значимо друг от друга выборочные оценки S_n, вычисленные в Таблицах 3.1 и 3.5. При уровне доверия, равном 95%, S₁ = 1,62 ммоль/л, S₂ = 1,19 ммоль/л, n₁ = 20и n₂ = 20из таблиц критических значений для статистики Фишера находим, что Fкрит = 2,20. И поскольку для этого случая F = 2,62 / 1,19 = 2,20, что не больше, чем Fкрит = 2,20, то согласно критерию Фишера полученные выборочные оценки истинного значения стандартного отклонения, равные соответственно 1,62 и 1,19 ммоль/л , не отличаются статистически значимо друг от друга. Это говорит о том, что эти выборочные значения стандартного отклонения характеризуют одно и тоже генеральное значение σ. Что, скорее всего, объясняется отсутствием значимых флуктуации или дрейфа калибровки АС за время проведения измерений.

Если установлено, что выбросов среди результатов установочной серии более нет, то тогда считают полученные выборочные значения для среднего (Хср)_n и стандартного отклонения S_n наилучшими оценками их истинных значений µ и σ. На основании полученного выборочного значения (Хср)_n вычисляют по нижеприведенной формуле оценочное эксплуатационное значение для систематического смещения В_n, которое является выборочной оценкой его истинного значения ∆:

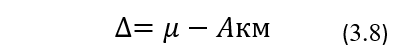
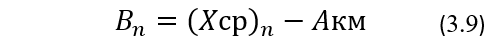
где Акм — паспортное значение уровня аналита в используемом контрольном материале. Как видно из формулы (3.9) показатель B_n, в отличие от показателя S_n, может иметь и положительные, и отрицательные значения.

Точность оценки генеральных значений математического ожидания μ и стандартного отклонения σс использованием соответственно выборочных значений среднеарифметического (Xср)_n и стандартного отклонения S_n логично определять по ширине их доверительных интервалов (далее – ДИ). Доверительным называют интервал, который содержит генеральное значение искомого параметра с заданной надежностью. Можно также сказать, что ДИ содержит с заданной надежностью все выборочные значения искомого параметра. При описании надежности обычно используют два термина: уровень значимости и уровень доверия. Уровень значимостиα, который обозначают обычно буквой α, — это вероятность, с которой генеральное значение параметра не попадает в доверительный интервал. Уровень доверия, который обычно обозначают буквой p, — это вероятность того, что доверительный интервал содержит генеральное значение искомого параметра. Таким образом p = 1 — α. Как правило, уровень значимости выбирают равным 0,01, 0,05 и 0,10, что соответствует уровню доверия 0,99, 0,95 и 0,90. Собственно поэтому ДИ часто называют интервальной оценкой искомого параметра. Очевидно, что чем меньше ширина ДИ для генерального значения искомого параметра, тем точнее его оценка. Из дальнейшего станет видно, что ширина ДИ уменьшается с ростом объема выборки n, поэтому чем больше объем выборки, тем меньше ширина ДИ. ДИ для генеральных значений µ и σ обычно обозначают так: µ_нг< µ < µ_вг   и   σ_нг < σ < σ_вг, где µ_нг иσ_нг являются нижними, а µ_вг и σ_вг — верхними границами ДИ для генеральных значений соответственно µ и σ.

Заметим, что размеры ДИ для генерального значения ∆ автоматически вытекают из формулы (3.8). Воспользуемся этой формулой и вышеупомянутым выражением ДИ для µ и тогда получим: µ_нг -Акм< µ — Акм < µ_вг — Акм или ∆_нг < ∆ < ∆_вг, где ∆_нг и ∆_вг являются нижней и соответственно верхней границами ДИ для генерального значения ∆.

Сначала определим степень точности оценки генерального значения μ его выборочными значениями (Xср)_n. Из математической статистики известно, что расчет нижней µ_нг(n) и верхней µ_вг(n) границ двусторонних ДИ для генерального значения µ проводится по формулам:

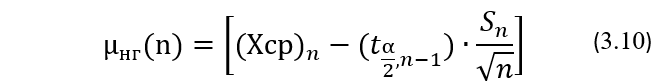
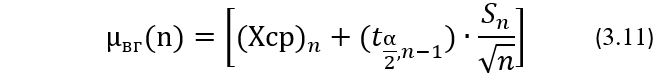
где t_{α/2, n-1} — квантили распределения Стьюдента, значения для которых можно найти в интернете или в справочниках по математической статистике; α – уровень значимости или, что тоже самое, значение вероятности выхода значения матожидания μ за пределы доверительного интервала; p=(1-α) – выбираемый уровень доверия, то есть доверительная вероятность попадания значения матожидания μ в пределы доверительного интервала; n — объем выборки; n-1 – число степеней свободы.

Двумя параметрами, задающими выбор значений квантилей из таблиц, являются обычно уровень значимости или доверительная вероятность и число степеней свободы. При выборе нужного значения из таблицы квантилей Стьюдента с уровнями значимости важно помнить, что в данной задаче рассматривается случай двустороннего доверительного интервала или, как иногда говорят, случай двусторонней гипотезы. Поэтому при выборе уровня доверия в 95%, то есть при выборе доверительной вероятности p = 1 – α = 0,95, что соответствует уровню значимости α=0,05, надо выбирать табличное значение квантиля Стьюдента из колонки для t_{α/2, n-1,} то есть из колонки t_{0,025; n-1}. Для удобства проведения расчетов в Таблице 3.6 приведены некоторые значения t_{α/2, n-1} для квантилей Стьюдента для двусторонних доверительных интервалов для разных доверительных вероятностей p и разного числа степеней свободы n-1.

Степень точности оценки генерального значения μ его выборочными значениями (Xср)_n будем определять по ширине его ДИ, а максимально возможную ошибку такой оценки будем определять отношением верхней границы ДИ к его нижней границе.

Покажем на примере типовой расчет границ ДИ для генерального значения µ, используя данные Таблицы 3.4, в которой количество n результатов повторных измерений, для вычислений (Хср)_n и S_n, равно 19. Это соответствует числу степеней свободы n – 1 = 19 – 1 = 18. Выбирая в Таблице 3.6 число степеней свободы равное 19, и выбирая доверительную вероятность равную 0,95, находим значение квантиля, которое будет равно t_{0,025; 18} = 2,101. Соответственно нижняя граница ДИ для генерального значения µ будет равна 144,70 — 2,101 * 1,18 / 4,36 = 144,7 — 0,57 = 144,13 ммоль/л, а верхняя – 144,7 + 0,57 = 145,27 ммоль/л. Таким образом, можно утверждать, что с 95% доверительной вероятностью генеральное значение µ будет находиться в диапазоне от 144,13 до 145,27 ммоль/л.

Теперь, вычитая из верхней границы доверительного интервала его нижнюю границу, получим формулу для определения ширины доверительного интервала ∆μ_n, которая, в свою очередь, при выбранном уровне доверия определяет точность оценки генерального значения математического ожидания μ по выборочному среднему (Хср)_n:

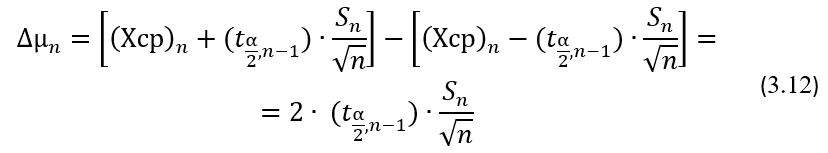
Как видно из формулы (3.12), ширина двустороннего доверительного интервала для генерального значения µ зависит только от выбранной доверительной вероятности, объема выборки n и выборочного значения стандартного отклонения S_n. Из математической статистики известно, что при значениях n>20 выборочные значения (Хср)_n и S_n также, как и значения квантилей Стьюдента, не изменяются существенно. Поэтому, исходя из формулы (3.12), можно сделать вывод, что точность оценки генерального значения μ с использованием выборочного значения среднего (Xср)_n возрастает пропорционально √n, то есть корню квадратному из объема выборки n.

Таблица 3.6. Таблица квантилей tα/2, n-1 распределения Стьюдента для случая двусторонней гипотезы.

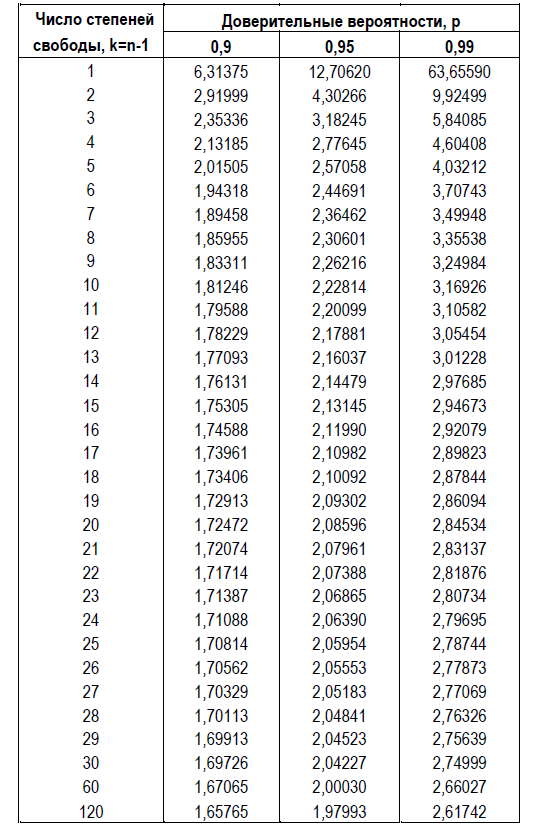
Ширину доверительного интервала ∆µ_n для генерального значения µ, рассчитываемую по формуле (3.11), удобнее представлять в относительных единицах, выражая ее в долях выборочного значения стандартного отклонения S_n по формуле:

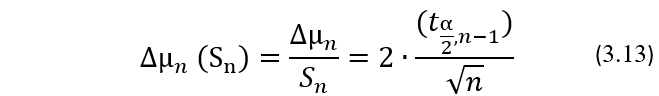
Из формулы (3.13) следует, что ширина доверительного интервала для µ в долях выборочного значения S_n зависит только от величины квантиля, практически не изменяющейся при n>20, и объема выборки, что очень удобно для визуализации степени точности интервальной оценки µ в зависимости от объема выборки n. Изменение ширины 95% доверительного интервала ∆μ_n (S_n) по мере увеличения объема выборки n приведена на Рис 3.1.

В качестве типового практического примера, воспользуемся данными Таблиц 3.4 и 3.6 и вычислим для них по формулам (3.12) и (3.13) в абсолютных и относительных единицах ширину 95% доверительного интервала ∆μ_n и ∆μ_n (S_n) для генерального значения µ: ∆µ₁₉  = 2 * 2,1 * 1,18 / √19 = 4,96 / 4,36 = 1,14 ммоль/л. Соответственно ∆μ₁₉ (S₁₉) = 2 * 2,1 / √19 = 4,2 / 4,36 = 0,96. При объемах выборки n=10, n=15, n=25 и n=30 для показателей точности интервальной оценки в долях S_n будем иметь: ∆μ₁₀ (S₁₀) = 2 * 2,26 / √10 = 4,52 / 3,16 = 1,43; ∆μ₁₅ (S₁₅) = 2 * 2,13 / √15 = 4,26 / 3,87 = 1,10; ∆μ₂₅ (S₂₅) = 2 * 2,06 / √25 = 4,12 / 5 = 0,82 и ∆μ₃₀ (S₃₀) = 2 * 2,04 / √30 = 4,08 / 5,47 = 0,75. То есть точность интервальной оценки генерального значения µ с помощью выборочной средней (Хср)_n при объеме выборки n=30 будет почти в 2 раза лучше, чем при объеме выборки n=10.

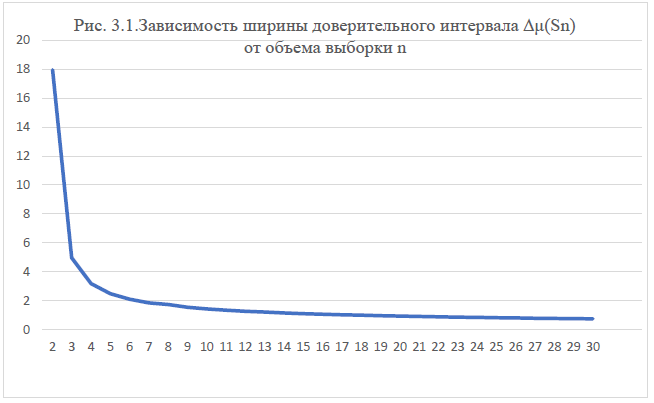
Рис. 3.1. Зависимость ширины доверительного интервала для генерального значения μ от объема выборки n в долях выборочного значения Sn стандартного отклонения σ.

Теперь перейдем к определению ширины ДИ для дисперсии σ², а затем и для стандартного отклонения σ.Из математической статистики известно, что нижняя σ²_нг(n) и верхняя σ²_вг(n) границы двустороннего доверительного интервала для дисперсии σ² при неизвестном генеральном значении µ вычисляются по формулам (3.14) и (3.15):

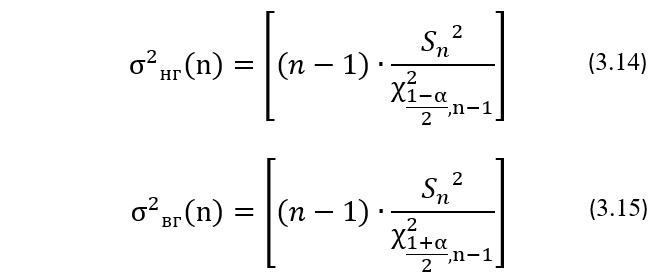
где α — доверительная вероятность, χ² _{(1-α)/2, n-1} и χ² _{(1+α)/2, n-1} — квантили распределения χ² (Хи-квадрат). Для удобства проведения расчетов некоторые значения квантилей χ² для разных доверительных вероятностей α и разного числа степеней свободы n-1 приведены в Таблице 3.7.

Исходя из своего определения, ДИ для дисперсии σ² и для стандартного отклонения σ будут выглядеть следующим образом:

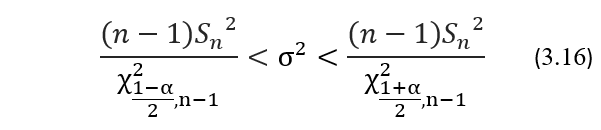
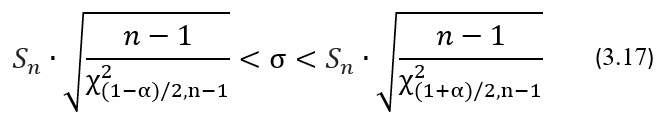
Степень точности оценки генерального значения σ его выборочными значениями S_n будем определять по ширине его ДИ, а максимально возможную ошибку такой оценки будем определять отношением верхней границы ДИ к его нижней границе.

Таблица 3.7. Таблица квантилей (критических значений) распределения Хи-квадрат.

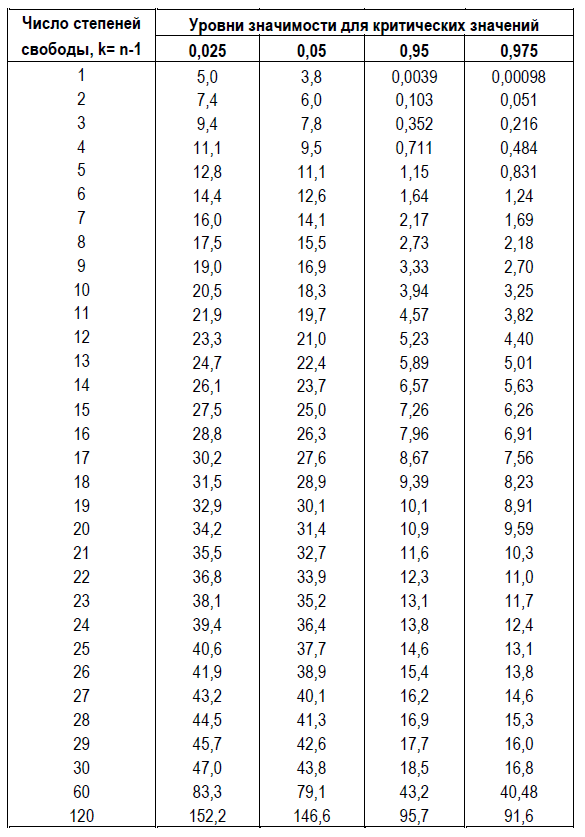
Теперь покажем на примере типовой расчет границ ДИ для генеральных значений σ² и σ, используя данные, приведенные в Таблице 3.4, в которой количество n результатов повторных измерений, для вычисления выборочного значения S_n, равно 19. Это соответствует числу степеней свободы n-1 = 19 — 1 = 18. Выбирая в Таблице 3.7 число степеней свободы равное 18, и используя доверительную вероятность α равную 0,95, находим в ней нужные значения квантилей, которые будут равны χ² _{(1-α)/2, n-1} = χ²[(1-0,95)/2, (19-1)] = χ² [(0,025), 18] =31,53 и соответственно χ² _{(1+α)/2, n-1} = χ²[(1+0,95)/2, (19-1)] = χ² [(0,975), 18] =8,23. Таким образом, рассчитываемые по формулам (3.14) и (3.15) нижняя и верхняя границы ДИ для генерального значения σ² будут равны σ²_нг(19)= 18 * 1,18 * 1,18 / 31,53 = 0,795 и соответственно σ²_вг(19) = 18 * 1,18 * 1,18 / 8,23 = 3,045. И в конечном итоге, получим ДИ для генерального значения стандартного отклонения σ в ммоль/л: 0,89 < σ < 1,75. Таким образом можно утверждать, что с 95% доверительной вероятностью генеральное значение σ будет находиться в диапазоне от 0,89 до 1,75 ммоль/л, хотя для выборочной оценки было получено значение S₍₁₉₎ = 1,18 ммоль/л. Теперь воспользуемся формулой (3.18) и на основе ширины соответствующего ДИ определим точность выборочной оценки генерального значения дисперсии σ² и стандартного отклонения σ. Ширина ДИ ∆σ_n² для дисперсии σ² будет равна:

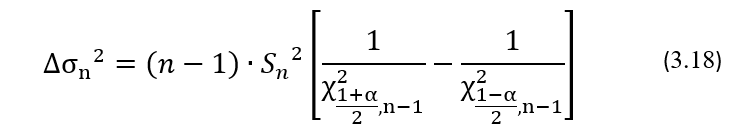
Соответственно ширина ДИ ∆σ_n для показателя σ будет равна разнице корней квадратных из верхней и нижней границ ДИ для дисперсии σ², а именно:

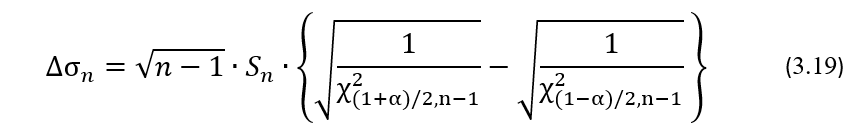
И, наконец, формула для расчета ширины ДИ ∆σ_n (S_n) для генерального значения σ в долях выборочного значения S_n будет иметь вид:

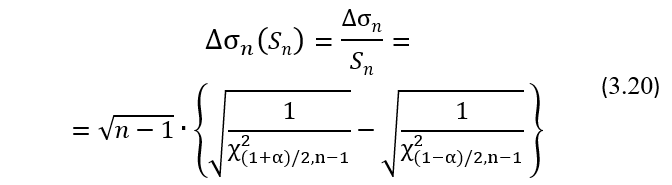
Динамика изменения ширины 95% доверительного интервала ∆σ_n (S_n) по мере увеличения количества n результатов повторных измерений представлена на Рис. 3.2.

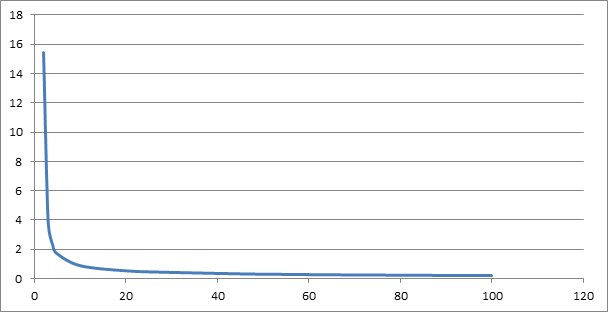
Рис. 3.2. Динамика изменения ширины доверительного интервала ∆σn (Sn) от объема выборки n в единицах стандартной ошибки Sn.

Как видно из Рис. 3.2, точность оценки генерального значения по его выборочным значениям изменяется просто драматически при уменьшении объема выборки с 20 до нескольких единиц. Так при 95% уровне доверия и при наличии выборки только из двух (n=2) результатов повторных измерений ширина ДИ для генерального о значения σ, оцениваемого в долях выборочной дисперсии S₂, оказывается близкой к 100*S₂, а генеральное значение σ, характеризующее случайную составляющую ошибки результатов, получаемых при использовании исследуемой аналитической системы, может реально иметь любое значение от 0,44*S₂  до 100*S₂. Таким образом, при наличии только двух результатов повторных измерений ошибка в оценке генерального значения σ по выборочному значению S₂ может достигать 100 / 0,44 =230 раз. Соответственно, при том же 95% уровне доверия в случае выборки объемом n=3 ширина ДИ для σ оказывается равной 5,76*S₃, а генеральное значение σ реально может иметь любое значение от 0,52*S₃ до 6,28*S₃. И таким образом, при наличии трех результатов повторных измерений ошибка в оценке генерального значения σ по выборочному значению S₃ может достигать 6,28 / 0,52 = 12 раз. При том же 95% уровне доверия и при выборке объемом n=10 ширина ДИ для σ оказывается равной 1,14*S₁₀,границы ДИ оказываются равными 0,69*S₁₀  и 1,83*S₁₀ , а ошибка в оценке генерального значения σ по выборочному значению S₁₀ может достигать 1,83 / 0,69 = 2,65 раз. При 95% уровне доверия и при выборках объемом n=20, которые обычно получают в установочных сериях, ширина ДИ для σ оказывается равной 0,70*S₂₀,границы ДИ оказываются равными 0,76*S₂₀  и 1,46*S₂₀, а ошибка в оценке генерального значения σ по выборочному значению S₂₀ может достигать 1,46 / 0,76 = 1,9 раз. Иными словами, используя полученное выборочное значение S₂₀ для оценки генерального значения σ, можно ошибиться почти в 2 раза. И, наконец, при 95% уровне доверия и при выборках объемом n=25, которые рекомендуется использовать руководством CLSI EP15-A3 для проведения выборочных оценок аналитических характеристик, ширина ДИ для σ оказывается равной 0,61*S₂₅,границы ДИ оказываются равными 0,78*S₂₅ и 1,39*S₂₅, а ошибка в оценке генерального значения σ по выборочному значению S₂₅ может достигать 1,39 / 0,78 = 1,8 раз.

Отдельно отметим, что при том же 95% уровне доверия и объемах выборки n=50; n=100; n=150; n=200; n=250 и n=300, максимальные ошибки в оценке генерального значения σ по их выборочным значениям могут составить соответственно 1,49; 1,32; 1,26; 1,22; 1,19 и 1,17 раз. Именно потому, что точность оценки генеральных значений μ и σ с использованием их выборочных значений (Хср)_n и S_n постоянно возрастает с ростом объема выборки n, все руководства по ведению внутрилабораторного контроля качества рекомендуют периодически (по мере накопления результатов повторных контрольных измерений) пересчитывать выборочные значения для µ и σ и использовать эти новые более точные оценки в качестве обновленных параметров контрольной карты. Обычно рекомендуют переопределять параметры контрольной карты через каждые последующие 20-30 контрольных результатов.

Еще раз напомним, что выборочные значения B_n и S_n являются только приблизительными оценками генеральных значений смещения ∆ и стандартного отклонения σ. И если повторить еще раз аналогичную серию повторных измерений количеством n, то скорее всего, для показателей B_n и S_n будут получены значения, отличные от полученных в первой серии, хотя, возможно, и близкие к ним. Причина такого отличия выборочных значений между собой заключается главным образом в том, что обе выборки имеют хотя и статистически значимый, но, тем не менее, ограниченный объем. Следует отметить, что при многократном повторении серий повторных измерений с одними тем же количеством n, получаемые на их основе выборочные значения будут с выбранной доверительной вероятностью попадать в ДИ для генерального значения соответствующего показателя. В этой связи, получаемые выборочные оценки B_n и S_n генеральных значений ∆ и σ следует использовать с учетом того, что они не абсолютно точно описывают последние и могут существенно отличаться от них, даже в разы.

В настоящей лекции описаны процедуры общепринятых технологий определения на практике эксплуатационных значений основных аналитических характеристик АС, а также рассмотрены вопросы точности определения этих значений.

Краткие выводы по Лекции 3.

1) Генеральные значения основных аналитических характеристик АС, к которым относятся систематическое смещение и стандартное отклонение, точно определять не представляется возможным. На практике эти значения только оценивают, используя для этого результаты повторных измерений ограниченного объема, которые, в свою очередь, получают в процессе проведения установочных серий.

2) При проведении установочной серии национальные руководства рекомендует проводить ежедневно по 1 измерению уровня аналита в контрольном материале в течение 20 рабочих дней, а международные — по 5 измерений ежедневно в течение 5 рабочих дней.

3) Результаты, полученные в установочной серии, в руководстве CLSI EP15-A3 рекомендуется проверять на отсутствие среди них грубых ошибок.

4) Генеральное значение систематического смещения аналитической системы за время проведения установочной серии может изменяться и даже существенно, что обычно обусловливается дрейфом и/или флуктуацией ее калибровки. В этой связи желательно проводить методом дупликатов дополнительную проверку адекватности выборочной оценки стандартного отклонения по данным, полученным при проведении установочной серии.

5) Используя полученные выборочные значения и выбранный уровень доверия, определяют границы доверительных интервалов для генеральных значений основных аналитических характеристик.

Литература к Лекции 3.

1. ГОСТ ISO/IEC 17025-2019. Общие требования к компетентности испытательных и калибровочных лабораторий.

2. Приказ МЗ РФ от 26.05.2003 №220 «Об утверждении отраслевого стандарта «Правила проведения внутрилабораторного контроля качества количественных методов клинических лабораторных исследований с использованием контрольных материалов». Приложение. «ОСТ 91500.13.0001-2003».

3. ГОСТ Р 53133.2-2008. Национальный стандарт РФ. Технологии лабораторные клинические. Контроль качества клинических лабораторных исследований. Часть 2. Правила проведения внутрилабораторного контроля качества количественных методов клинических лабораторных исследований с использованием контрольных материалов.

4. Clinical and Laboratory Standards Institute «User Verification of Precision and Estimation of Bias». CLSI Guideline. Document EP15-A3. September, 2014.

5. ГОСТ Р 8.736-2011. Государственная система обеспечения единства измерений (ГСИ). Измерения прямые многократные. Методы обработки результатов измерений. Основные положения.

6. Вентцель Е.С. Теория вероятностей. — 4-е изд. — М.: Наука, 1969. — 576 c.

---

Скачать Лекцию 3