Лекция 10. Алгоритмы сравнения результатов лабораторных исследований

М.И.Прищепа, кандидат технических наук, ЗАО «АНАЛИТИКА»

В этой лекции будет рассматриваться один из самых важных вопросов практической лабораторной метрологии, а скорее всего важнейший из них. Ибо речь в ней пойдёт о современных рекомендациях и правилах использования результатов исследований биопроб в медицинских лабораториях и клиниках. Особое внимание в лекции будет уделено тому, почему при использовании лабораторных результатов надо не просто сравнивать измеренные значения уровней аналитов между собой или с уровнями принятия клинических решений, но обязательно учитывать их возможную вариабельность. Величина вариабельности, как будет показано ниже, зависит как от аналитических и преаналитических процедур, так и от биологических изменений уровня исследуемого аналита, внутренне присущих жизнедеятельности человеческого организма. Перечисленные факторы могут существенно влиять на результаты проводимых исследований и тем самым искажать информацию о реальном содержании аналита в биожидкости пациента in vivo, что в конечном итоге может приводить и зачастую приводит к ошибкам как при постановке диагноза, так и при оценке эффективности проводимой терапии.

Но даже при всем при этом статистический анализ клинического использования результатов лабораторных исследований показывает, что именно они являются объективной основой для почти 70% случаев принятия клиницистами своих решений [1,2]. Это действительно достаточно высокий показатель, подчёркивающий растущую значимость лабораторных результатов для решения клинических задач.

Итак, отметим еще раз, что на адекватность оценки текущего состояния пациента и эффективности проводимой терапии оказывают влияние не только значения результатов исследований, но и величины их ошибок, зависящие, в свою очередь, от качества проводимых аналитических и преаналитических процедур. Это, во-первых. Во-вторых, на адекватность таких оценок не менее существенное влияние оказывает и биологическая вариация уровня исследуемого аналита in vivo. Поэтому простое сравнение измеренных значений между собой или с уровнями принятия клинических решений может действительно приводить к неправильным клиническим выводам. И особенно в тех случаях, когда величины перечисленных выше вариаций сравнимы по величине с измеряемым уровнем аналита.

Рассмотрим последовательно возможное влияние перечисленных факторов на интерпретацию полученных результатов и, в конечном итоге, на принятие клинических решений. Сначала оценим степень влияния аналитической вариации измеряемого уровня аналита, а затем его биологической вариации. Из-за отсутствия в настоящее время справочных данных о величине преаналитической вариации ее возможное влияние отдельно в этой лекции рассматриваться не будет. Это никоим образом не скажется значимо на итогах проводимого анализа, поскольку справочные данные о внутрииндивидуальной биологической вариации в некотором смысле включают в себя автоматически и преаналитическую вариацию.

Переходя к оценке степени влияния аналитической вариации на адекватность клинической оценки, отметим прежде всего, что результаты измерений уровня аналита в пробах пациентов, полученные даже на самых современных аналитических системах (далее – АС), всегда имеют систематические и случайные ошибки и порой даже немалые. Что обуславливается природой измерений как таковой. Результаты измерений, а в особенности результаты сложных измерений, к которым относятся практически все количественные лабораторные тесты, в принципе не могут быть абсолютно точными. Они всегда являлись и будут являться только приблизительными оценками измеряемой физической величины. То есть результаты измерений, получаемые на любой АС, описывают фактический уровень аналита в исследуемой пробе далеко не с абсолютной точностью, а лишь с некоторой ошибкой или, как говорят метрологи, с той или иной погрешностью. В итоге лабораторные результаты всегда или завышают, или занижают фактические значения уровня аналита в пробах пациента, порой превращая фактическую патологию в норму, и наоборот фактическую норму превращают в патологию, вводя тем самым клиницистов в заблуждение. Поскольку измеряемый уровень аналита в исследуемой пробе всегда подвержен в той или иной степени аналитической вариации, то очевидно, что этот факт, во избежание неадекватных выводов о состоянии пациента, нельзя не учитывать при клиническом использовании лабораторных результатов.

Рассмотрим далее общепринятые способы оценки возможного влияния аналитической вариации на результаты измерения уровня аналита в исследуемых пробах. Отметим прежде всего, что в настоящее время неточность лабораторной оценки фактических уровней аналита в биопробах все чаще характеризуют так называемой полной ошибкой. Последняя характеризует максимально возможное отклонение результата измерения от фактического значения уровня аналита в исследуемой пробе. Напомним, что величина полной ошибки результатов измерений, получаемых на конкретной АС, определяется эксплуатационными значениями ее аналитических характеристик (далее – АХ), таких как систематическое смещение В_ас и стандартное отклонение S_ac. Для конкретной АС значения полной ошибки, которую, как и в предыдущих лекциях будем обозначать как ТЕ_ас, вычисляются по следующей формуле:

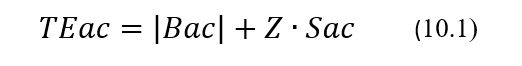
где |В_ас| – модуль или абсолютное значение показателя В_ас, а Z – значение так называемого показателя Z-score, которое зависит от доверительной вероятности и вида доверительного интервала, выбираемых для оценки фактических значений уровня аналита в исследуемых пробах на основе полученного результата измерения. Хотя в лабораторной медицине обычно принято использовать доверительную вероятность, равную 95%, но в некоторых особых случаях могут потребоваться уровни доверия, равные 90% или 99%. Вид же доверительного интервала для оценки фактического значения, который в общем случае может быть односторонним или двусторонним, зависит главным образом от соотношения эксплуатационных значений В_ас и S_ас, а также отчасти от выбранной доверительной вероятности. Обычно, если значение В_ас существенно меньше значения S_ac, то тогда доверительный интервал следует выбирать двусторонним, а если значение В_ас сравнимо со значением S_ac, то есть несколько меньше или больше значения S_ac, то тогда доверительный интервал следует выбирать односторонним. Нужные значения показателя Z-score можно найти в справочниках по математической статистике или определить самостоятельно, используя специальные компьютерные приложения. Некоторые значения показателя Z-score – в качестве примера – приведены в таблице 10.1.

В случаях, рассматриваемых в этой лекции, значения Z показателя Z-score по своей сути просто показывают в скольких стандартных отклонениях Sac от своего генерального среднего будут лежать соответственно 95%, 90% или 99% результатов повторных измерений уровня аналита в одной и той же биопробе. В случаях, когда систематическое смещение В_ас используемой АС окажется весьма близким к нулю, то тогда упомянутые процентные доли результатов повторных измерений будут располагаться симметричным образом по разные стороны уже не только от своего генерального среднего, но и от фактического значения уровня аналита в исследуемой пробе. Собственно говоря, такое распределение результатов повторных измерений и будет представлять собой некую типичную картину так называемой аналитической вариации измеряемого уровня аналита. В силу природы измерений определить фактическое значение уровня аналита в исследуемой пробе абсолютно точно невозможно. Можно только судить о нем приблизительно по полученному результату измерения. И как видно из формулы (10.1), в случае, когда значение показателя В_ас будет равно нулю, то тогда результаты повторных измерений уровня аналита в исследуемой пробе будут с соответствующей доверительной вероятностью отклоняться от фактического значения на величину не свыше произведения Z*S_ac. То есть можно будет полагать, что на выбранном уровне максимальная разница между полученным результатом измерения уровня аналита и его фактическим значением в исследуемой пробе будет равна Z*S_ac. Поскольку значение смещения В_ас мы предполагаем равным нулю, то соответственно полученный результат измерения может отклониться от фактического значения как в большую, так и в меньшую сторону максимум на величину Z*S_ac. В свою очередь это также будет означать, что фактическое значение может отличаться от результата измерения в большую или меньшую от него сторону максимум на такую же величину, то есть равную Z*S_ac. Таким образом фактическое значение уровня аналита будет находиться где-то внутри границ интервала

Х_изм–Z*S_ac и Х_изм+Z*S_ac, где Х_изм – полученный результат измерения. Такой интервал, показывающий местонахождение фактического значения, по понятным причинам принято называть доверительным. При этом в случае, когда близкое к нулю эксплуатационное значение В_ас оказываясь одновременно значительно меньше значения Sac, доверительный интервал для фактического значения следует выбирать, как было упомянуто выше, двусторонним. Тогда и конкретное значение показателя Z-score следует выбирать для двустороннего интервала, которое будет зависеть также и от выбираемого уровня доверия. Например, выбрав 95% уровень доверия к лабораторной оценке фактического значения, найдём из таблице 10.1, что значение Z для двусторонних доверительных интервалов будет равно 1,96, а для односторонних – 1,65.

Примечание 10.1. При рассмотрении всех вопросов в этой лекции автоматически подразумевается неизменность аналитических характеристик АС в процессе ее эксплуатации.

Примечание 10.2. Во избежание необходимости подстраивать границы референтного диапазона для результатов, получаемых на новой, отремонтированной или обновленной АС (после перехода на реагенты и/или калибраторы другого лота), лаборатории в настоящее время перед выдачей результатов в клинику все чаще корректируют их на величину систематического смещения В_ас. Эффективно это как раз и соответствует АС, которая имеет систематическое смещение, равное нулю.

Таблица 10.1. Значения показателя Z-score для типовых доверительных вероятностей.

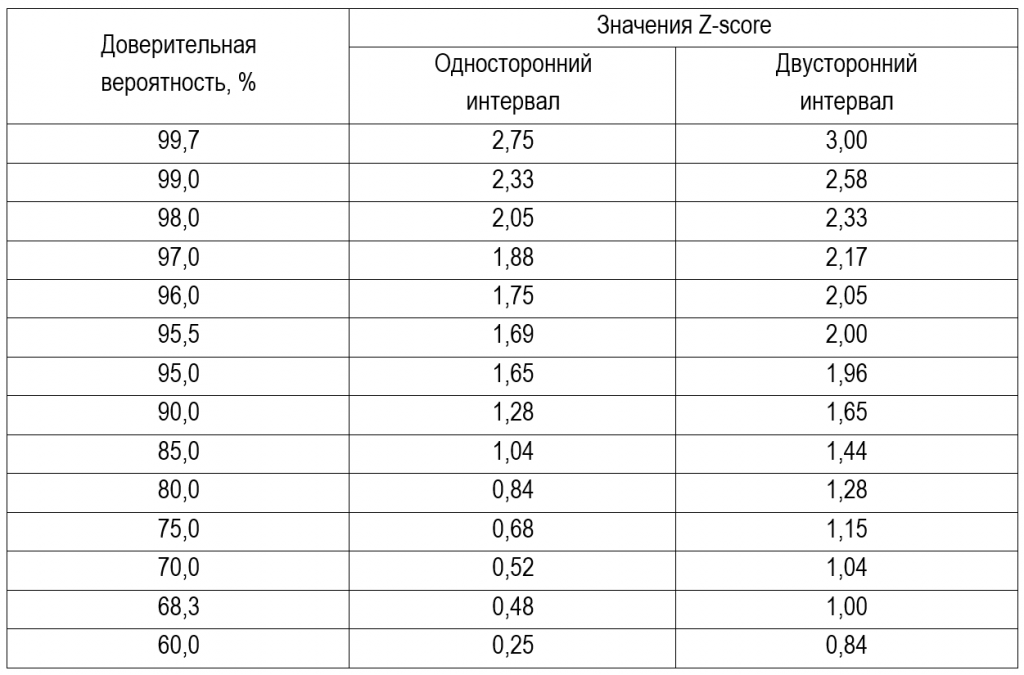
Пример 10.1. Оценим максимально возможное отклонение результата измерения уровня аналита от его фактического значения для типовой АС, используемой в лаборатории для измерения глюкозы в сыворотке крови. Предположим, что после проведения на АС установочной серии для нее были получены следующие эксплуатационные значения: В_ас = +0,06 ммоль/л и S_ac = 0,15 ммоль/л. Причем для всего диапазона измерений АС, хотя на практике так бывает далеко не всегда. Используя формулу (10.1), вычислим для 95% уровня доверия значение полной ошибки для полученных результатов и получим, что ТЕ_ас = 0,06+1,96*0,15 = 0,35 ммоль/л. То есть на выбранном уровне доверия фактический уровень аналита может отличаться от измеренного вплоть до 0,35 ммоль/л как в большую, так и в меньшую от него сторону. Предположим, что результаты измерения уровня глюкозы в сыворотке в последовательно взятых у пациента пробах оказались равными Х₁ = 5,21 ммоль/л – для первой пробы и Х₂ = 5,41 ммоль/л – для последующей пробы. Тогда с вероятностью 95% фактическое значение уровня глюкозы для первой пробы будет находиться где то внутри доверительного интервала с границами 4,86–5,56 ммоль/л. Соответственно для второй – где-то внутри интервала с границами 5,06–5,76 ммоль/л. Иначе говоря, для таких уровней аналита, то есть близких к 5 ммоль/л, на 95% уровне доверия фактическое значение может отличаться от измеренного как в меньшую, так и в большую от него сторону вплоть до 7% = 100*0,35/5.

Чтобы не подстраивать границы референтного диапазона для полученных результатов, поскольку используемая АС имеет ненулевое значение смещения В_ас, скорректируем полученные результаты на величину систематического смещения АС, то есть вычтем из каждого результата 0,06 ммоль/л. Тогда получим, что «несмещённые» результаты измерения уровня глюкозы, то есть как если бы значение В_ас у АС было бы равно нулю, будут соответственно равны 5,15 ммоль/л и 5,35 ммоль/л соответственно. Теперь, используя формулу (10.1), оценим для 95% уровня доверия значение показателя ТЕ_ас» для «несмещенных» результатов и получим, что при В_ас» равным нулю это значение будет равно ТЕ_ас» = Z*S_ac = 1,96*0,15 ммоль/л = 0,29 ммоль/л. Тогда для первого скорректированного результата, равного 5,15 ммоль/л, с вероятностью 95% фактическое значение будет находиться где-то внутри доверительного интервала с границами 4,86 ммоль/л и 5,44 ммоль/л, оставаясь при этом, естественно, неизвестным. Соответственно для второго скорректированного результата, равного 5,35 ммоль/л, с вероятностью 95% фактическое значение будет находиться где-то внутри доверительного интервала с границами 5,06 ммоль/л и 5,64 ммоль/л, оставаясь при этом также неизвестным. Для уровней аналита, близких к 5 ммоль/л, на 95% уровне доверия фактическое значение может отличаться от скорректированного, то есть «несмещенного» результата как в меньшую так и в большую сторону вплоть до 6% = 100*0,29/5, что очевидно – поскольку для скорректированных результатов систематическое смещение равно нулю – оказалось несколько меньше аналогичного показателя для нескорректированных, то есть «смещенных» результатов измерения. Обращаем еще раз внимание на то, что фактические значения при этом могут быть как больше, так и меньше измеренных. Например, фактическое значение уровня глюкозы в первой пробе может оказаться равным 5,41 ммоль/л, а фактичекское значение во второй – равным 5,21 ммоль/л. Таким образом вполне может реализоваться ситуация, когда второй результат измерения на 0,2 ммоль/л больше первого, невзирая на то, что фактический уровень глюкозы во второй пробе на 0,2 ммоль/л меньше, чем в первой пробе. Чтобы лабораторные результаты не вводили клиницистов в заблуждение, последние должны быть проинформированы лабораторией о всех таких возможных ситуациях!

Теперь разберемся, что является причиной биологической вариации уровня аналита in vivo и каким образом она может влиять на принятие клинических решений. Как известно, уровни аналитов вследствие происходящих процессов обмена веществ в организме здорового человека совершают колебания вокруг своих гомеостатических точек (homeostatic set point) в определенных для каждого аналита пределах. Полный цикл колебаний уровня аналита вокруг своей гомеостатической точки происходит в течение характерного для него времени. Все это в конечном итоге и обуславливает наличие биологической вариации содержания аналита в биожидкостях in vivo. Иначе говоря, уровень любого аналита in vivo всегда подвержен некоей биологической вариации, внутренне присущей каждому здоровому индивиду. Заметим, что конкретные моменты достижения уровнем аналита своей гомеостатический точки для обследуемого индивида заранее неизвестны. Хотя в настоящее время и предполагается, что полный цикл колебаний для большинства аналитов происходит за сутки, но этот вопрос требует дальнейшей практической проверки. Так, например, до сих нет экспериментальных доказательств, что в тот или иной конкретный момент суток уровень хоть какого-либо аналита in vivo у здорового индивида имеет одно то тоже значение. Соответственно пока нет объективных оснований считать, что фактические уровни аналитов в пробах здорового пациента, взятых в одно и тоже время суток, будут всегда иметь одни и те же значения. Экспериментальные исследования по подобным вопросам уже начали проводиться. Так, например, в некоторых из них было показано, что параметры колебаний уровней аналитов в биожидкостях здоровых индивидуумов, в том числе их гомеостатические точки и амплитуды, могут зависеть от таких факторов как генетика индивида, диета, физическая нагрузка и возраст [3,4]. В любом случае сейчас уже достаточно очевидно, что измеряемые уровни аналитов подвержены не только аналитической вариации, что обуславливается природой измерительных процедур, но и биологической вариации, внутренне присущей человеческому организму. Следует отметить, что накапливать количественную информацию о биологических вариациях уровней аналита in vivo дело действительно весьма и весьма затратное и трудоемкое. Так база данных по этим вариациям стала формироваться уже более 50 лет тому назад, причем она постоянно расширяется, а ее данные постоянно уточняются. Начиная с конца прошлого столетия и вплоть до 2014 года, то есть в течение приблизительно 15 лет, наиболее полная база данных по биологическим вариациям с регулярным их обновлением поддерживалась Джеймсом Вестгардом [5]. Начиная с 2014 года поддержание базы данных по биологическим вариациям взяла на себя Европейская федерация по лабораторной медицине (EFLM), вернее специально созданная ею рабочая группа по биологическим вариациям [6]. К настоящему моменту самая последняя обновлённая и дополненная база данных по биологическим вариациям была опубликована членами этой группы отдельным документом [7] в феврале 2022 года. Данные по внутрииндивидуальной биологической вариации уровней аналитов в биожидкостях in vivo играют все большую и большую роль в лабораторной и клинической медицине. Их все возрастающую важность трудно переоценить. В последнее время появились даже предложения определять с их помощью постепенно от аналита к аналиту индивидуальные референтные диапазоны, которые в будущем смогли бы заменить текущие межиндивидуальные референтные диапазоны, приводимые в справочниках. Подобные исследования уже проводятся при формировании биологических паспортов для спортсменов. Что касается лабораторной медицины, то уже общепринятым стало использование данных по биологическим вариациям для разработки требований к АХ АС в качестве критерия их допуска к использованию в лабораториях. В частности, уже стало международным стандартом известное требование к стандартному отклонению АС, который не должен превышать половины аналогичного показателя внутрииндивидуальной биологической вариации. В результате в лабораторной практике стало нормой то, что количественный показатель аналитической вариации измеряемого уровня аналита не превышает половины аналогичного показателя его внутрииндивидуальной биологической вариации. Поскольку результаты измерений уровней аналитов подвержены подобным вариациям – в той или иной степени, но всегда – клиницистам при использовании лабораторных результатов следует принимать свои решения, полагаясь не только на измеренные значения уровней аналитов, но также учитывая возможное влияние на них аналитической и биологической вариаций. Конечно, если количественные показатели таких вариаций были бы существенно меньше измеренных значений уровня аналита, то тогда для интерпретации клинических случаев вполне можно было бы ограничиться использованием только самих результатов. Но такие случаи на практике если и встречаются, то весьма редко.

Основной принцип использования лабораторных результатов должен состоять в следующем. Прежде всего следует помнить о том, что если обследуемый пациент абсолютно здоров и к нему не применяют никакого терапевтического воздействия, то и в таком случае результаты измерения уровня аналита в его пробах подвергаются аналитической и биологической вариациям. Именно это является причиной их отличия друг от друг, хотя и в определенных пределах. Так или иначе величина этих пределов вполне конкретна и определяется как параметрами вышеупомянутых вариаций, так и выбираемым уровнем доверия. Поэтому, если в какой то момент наблюдения за пациентом текущий результат станет отличаться от любого из предыдущих свыше этих пределов, то тогда можно будет с выбранной доверительной вероятностью предположить, что такое «запредельное» отличие результатов уже нельзя объяснить только их аналитической и биологической вариацией. И что скорее всего причиной такого «запредельного» отличия результатов будет являться изменение состояния обследуемого пациента.

Для того, чтобы уяснить себе каким образом можно оценивать величину допустимого предела отличия между собой результатов измерения уровня аналита в пробах здорового пациента, совершим краткий экскурс в основы математической статистики и теории измерений и обратим внимание на некоторые важные для рассматриваемого вопроса положения. Прежде всего отметим, что результат измерения уровня аналита в пробе любого пациента по своей природе является случайной величиной. Вследствие чего даже результаты повторных измерений уровня аналита в одной и той же пробе будут практически всегда отличаться друг от друга. Тем не менее эти результаты будут распределяться неким симметричным образом вокруг своего математического ожидания (МО) с некоторой дисперсией σ², характеризующей величину их разброса. На практике, как известно, величина дисперсии результатов повторных измерений уровня аналита в одной и той же биопробе оценивается с помощью стандартного отклонения S используемой АС по формуле: σ² = S², а величина их математического ожидания оценивается с помощью среднего Х_ср повторных результатов, то есть по формуле: МО = Х_ср. Продолжая экскурс, отметим одно из важных сейчас для нас свойств дисперсии, из которого следует, что дисперсия сложной случайной величины, которая представляет собой сумму или разность независимых случайных величин, равна сумме их дисперсий. Воспользуемся этим свойством для определения дисперсии результатов измерений уровня аналита в пробах, последовательно взятых у одного и того же здорового пациента, имея в виду, что такие результаты представляют собой реализацию сложной случайной величины, представляющей собой сумму простых случайных величин, одна из которых реализуются в виде совокупности уровней аналита в биожидкости здорового пациента in vivo, флуктуирующих вокруг своей гомеостатической точки, обуславливая таким образом их внутрииндивидуальную биологическую вариацию, другая – в виде совокупности уровней аналита в пробах, взятых у пациента почти в одно и тоже время, обработанных и доставленных в лабораторию к месту проведения их исследований, обуславливая таким образом их преаналитическую вариацию, и, наконец, третья – в виде результатов повторных измерений уровня аналита в одной и той же пробе, обуславливая таким образом их аналитическую вариацию. Исходя из вышеизложенного можно сделать вывод, что результаты измерений уровня аналита в пробах, последовательно взятых у одного и того же здорового пациента, будут распределяться также неким симметричным образом вокруг своего математического ожидания, то есть вокруг некой средней точки, с некоторой результирующей дисперсией, которая в общем случае будет определяться суммой трех дисперсий, одна из которых связана с внутрииндивидуальной биологической вариацией, другая – с преаналитической и, наконец, третья – с аналитической вариацией. Соответствующая формула для вычислений значений этой результирующей дисперсии будет приведена чуть ниже. Сейчас же отметим, что путем соблюдения однотипности процедур при проведении преаналитического этапа соответствующую ему дисперсию можно значительно снизить и сделать ее существенно меньше остальных двух дисперсий. Это, во-первых. Во-вторых, видимо вполне логично будет предположить, что справочные значения коэффициентов внутрииндивидуальной биологической вариации уровней аналитов in vivo, полученные в результате специально проведенных исследований и собранные в соответствующие базах данных, например в [5], уже включают в себя и преаналитические вариации. В этой связи будем здесь и далее в этой лекции полагать, что вариабельность результатов из-за преаналитических процедур пренебрежительно мала по сравнению с величинами биологической и аналитической вариаций.

Примечание 10.3. К основным источникам преаналитической вариации измеряемого уровня аналита обычно относят: а) разное время суток взятия проб пациента, б) прием пищи вместо голодания накануне взятия пробы, в) наличие физических нагрузок перед взятием пробы, г) использование стимуляторов при взятии пробы, д) разные позы пациента во время взятия проб,  е) разные вены в качестве источников проб, ж) разные типы используемого антикоагулянта, консерванта или стабилизатора, з) разная длительность наложения жгута перед взятием пробы, и) разные время и температура при транспортировке проб, к) разные время и скорость центрифугирования и, наконец, л) разные условия хранения проб до их анализа. И тем не менее, минимизировать величину преаналитической вариации вполне возможно, если а) стандартизовать условия взятия пробы, включая позу пациента, б) следовать утвержденным стандартам процедур флеботомии, включая длительность наложения жгута и способы взятия проб, и, наконец, в) придерживаться принятым стандартам транспортировки, хранения и обработки проб, включая их центрифугирование.

В качестве меры аналитической и биологической вариаций в лабораторной медицине, как известно, используются как стандартные отклонения, так и коэффициенты вариации. Последние по своей сути представляют собой относительные значения стандартных отклонений, вычисляемые в процентах по отношению к уровню аналита либо в исследуемой пробе, либо в его гомеостатической точке in vivo. Далее на конкретных примерах будет показано каким образом измеренные значения уровней аналитов и количественные показатели их аналитической и биологической вариаций следует использовать при проведении сравнения результатов с границами референтных диапазонов и между собой.

Начнем с использования измеренных значений. Как отмечалось в примечании 10.2, в последние годы во избежание необходимости подстраивать границы референтного диапазона при каждом вводе в эксплуатацию новой, либо отремонтированной, либо обновленной АС лаборатории перед выдачей результатов в клинику все чаще корректируют их на величину систематического смещения АС, вводимой в эксплуатацию. Фактически это соответствует тому, что вводимая в эксплуатацию АС как бы имеет нулевое систематическое смещение. И тогда скорректированные таким образом результаты измерений уровня аналита в пробах, последовательно взятых у одного и того же здорового пациента, не будут иметь систематического смещения относительно своего генерального среднего. То есть они будут распределяться симметричным образом вокруг этого генерального среднего, которое, в свою очередь, будет совпадать с гомеостатической точкой, соответствующей уровню исследуемого аналита in vivo. Хотя, как показывает опыт [8], такое распределение результатов является логарифмически нормальным, главным образом из-за их биологической вариации, мы все же в этой лекции будем для простоты считать его просто нормальным, что на самом деле, как оказывается [8], не сильно искажает реальную картину. Тогда стандартное отклонение S_abv распределения таких результатов, то есть результатов измерения уровня аналита в пробах, последовательно взятых у одного и того же здорового пациента, будет определяться суперпозицией стандартных отклонений аналитической и биологической вариаций. Вычисляться значения стандартного отклонения S_abv будут по известной формуле сложения дисперсий, подобной той, о которой шла речь и в предыдущих лекциях, а именно:

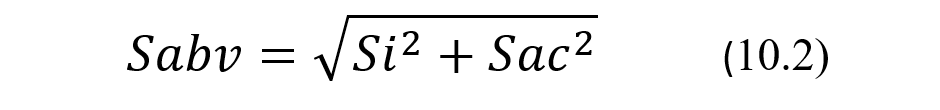
где S_abv — стандартное отклонение результатов измерения уровня аналита в пробах, последовательно взятых у одного и того же здорового пациента, S_i и S_ac – стандартные отклонения соответственно внутрииндивидуальной биологической и аналитической вариаций. Отметим еще раз, что хотя складывать дисперсии таким образом не совсем корректно, поскольку вариабельность уровней аналитов в биожидкостях здорового индивидуума подчиняется на самом деле не нормальному, а логарифмически нормальному закону распределения, тем не менее для простоты, как и упоминалось выше, будем здесь использовать именно такую формулу для сложения аналитической и биологической дисперсий. Тем более, что и на самом деле такое упрощение не очень сильно искажает реальную картину [8]. Тогда соответствующий коэффициент вариации CV_abv будет вычисляться по формуле:

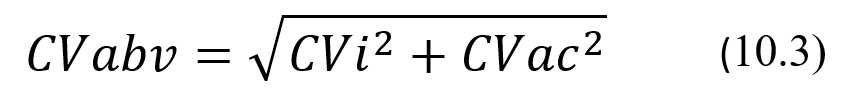
где CV_abv – коэффициент вариации результатов измерения уровня аналита в пробах, последовательно взятых у одного и того же здорового пациента, CV_i — коэффициент внутрииндивидуальной биологической вариации и CV_ac — коэффициент межсерийной аналитической вариации результатов повторных измерений уровня аналита в одной и той же пробе. Заметим, что коэффициент вариации CV_i, значения именно которого обычно приводятся в базах данных по биологическим вариациям уровней аналитов в биожидкостях in vivo, связан со стандартным отклонением S_i очевидно по формуле:

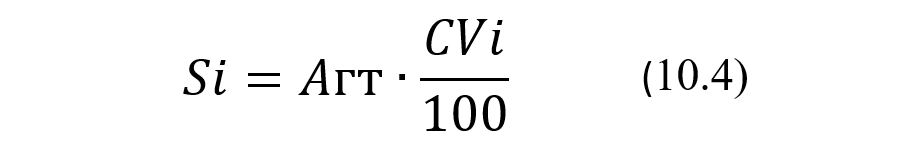
где S_i и CV_i – соответственно стандартное отклонение и коэффициент внутрииндивидуальной биологической вариации, а A_гт – значение уровня аналита, соответствующее его гомеостатической точке. Что касается связи показателей S_aс и CV_ac, то напомним, что если стандартное отклонение S_aс, определенное по данным установочной серии, является константой во всем диапазоне измерений АС, то тогда коэффициент аналитической вариации следует рассчитывать по формуле: CV_ac = 100*S_ac/Х_ист, где Х_ист – истинное или фактическое значение для уровня аналита в исследуемой пробе. На практике коэффициент аналитической вариации результатов повторных измерений оценивают по формуле: CV_ac = 100*S_ac/Х_изм, где Х_изм – результат измерения уровня аналита в текущей пробе. То есть предполагают, что Х_изм является наилучшей оценкой Х_ист, хотя их отличие иногда может быть и существенным. В этой связи отметим, что если формула (10.2) справедлива практически всегда для вычисления значений результирующего стандартного отклонения, то формула (10.3) для вычисления значений результирующего коэффициента вариации справедлива только в тех случаях, когда измеряемый уровень аналита Х_ист не сильно отличается от своей гомеостатической точки A_гт. В противном случае во всех расчетах и в самих процедурах сравнения результатов следует использовать только стандартные отклонения S_i и S_ac, а формулу (10.3) и соответственно коэффициенты вариации CV_i и CV_aс использовать в расчетах и в процедурах сравнения нельзя.

Примечание 10.4. Следует также отметить, что формула (10.3) для расчета значений коэффициента вариации CV_abv справедлива только для общепринятых на практике способов анализа, то есть, когда у пациента после назначения врача берут только одну биопробу для исследований, которая для получения результата анализируется только один раз. На самом деле значение этого показателя при необходимости может быть уменьшено как за счет увеличения кратности измерений при анализе одной пробы, так и за счет увеличения общего числа исследуемых проб. То есть за счет увеличения числа анализируемых проб, которые берутся у пациента в разное время суток, и за счет увеличения кратности измерений уровня аналита в каждой из них. Соответственно, если увеличить кратность измерений при анализе уровня аналита в каждой из проб, взятых у пациента в разное время суток, то для вычисления результирующего коэффициента суперпозиции этих вариаций надо будет вместо формулы (10.3) использовать следующую слегка более усложненную формулу:

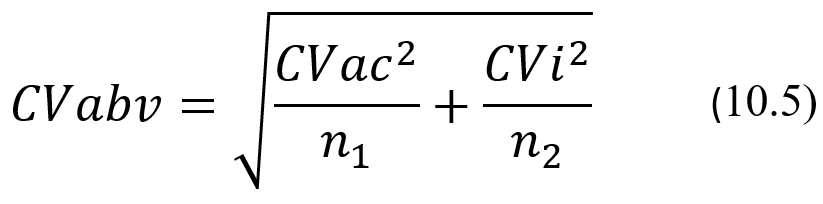
где n₁ – кратность измерений при анализе каждой пробы, а n₂ – количество проб, взятых у пациента в разное время суток, в каждой из которых уровень аналита определяется с кратностью измерений n₁. Интересно также отметить, что увеличение кратности измерений при проведении анализа пробы снижает коэффициент аналитической вариации не прямо пропорционально этой кратности, а только как корню квадратному из нее. То есть, если анализировать каждую пробу дважды, то это снизит коэффициент аналитической вариации по сравнению с однократным измерением не в 2 раза, а только в √2 раз, то есть уменьшит его не на 50%, а только на 30%. Соответственно, если исследовать каждую пробу трижды, то это снизит коэффициент аналитической вариации по сравнению с однократным измерением не в 3 раза, а только в √3 раз, то есть уменьшит его только на 42%. Ну и, наконец, если анализировать каждую пробу четырежды, то это позволит снизить коэффициент аналитической вариации по сравнению с однократным измерением не в 4 раза, а только в 2 раза, то есть на 50%. Аналогичная ситуация реализуется и при увеличении числа исследуемых проб пациента.

Пример 10.2. Оценим по формулам (10.2) и (10.3) значения показателей S_abv и CV_abv для типовой АС, используемой в лаборатории для измерения глюкозы в сыворотке крови. Предположим, что АС имеет следующие эксплуатационные значения для своих АХ: В_ас = +0,11 ммоль/л и S_ac = 0,14 ммоль/л, которые являются константами для всего диапазона измерений. Отметим, что так на практике бывает далеко не всегда. Предположим также, что результат измерения уровня глюкозы в сыворотке оказался равным 5,2 ммоль/л. Скорректируем его на величину систематического смещения АС, то есть вычтем из полученного результата 0,11 ммоль/л. Тогда получим, что скорректированный результат измерения уровня глюкозы в пробе, «несмещённый» относительно своего фактического значения, будет равен 5,09 ммоль/л. Это достаточно близко к гомеостатической точке уровня глюкозы здорового пациента, равной приблизительно 5,0 ммоль/л [11]. Теперь, используя перечисленные выше данные, вычислим в процентах относительное значение систематического смещения, которое будем далее обозначать как В_ас(%), и относительное значение стандартного отклонения, то есть значение показателя CV_ac. Соответственно получим: В_ас(%) = 100*В_ас/5,09 = 2,16%, и CV_ac = 100*S_ac/5,09 = 2,75%. Используя базу данных [5] найдем, что коэффициент внутрииндивидуальной биологической вариации уровня глюкозы в сыворотке CV_i будет равен 5,6%. Соответственно показатель CV_a как предельно допускаемое значение (далее – ПДЗ) для CV_ac будет равен половине показателя CV_i, то есть 2,8% и, наконец, показатель В_а(%) как ПДЗ для В_ас(%) будет равен 2,34%. Откуда следует, что упомянутые выше эксплуатационные значения АХ соответствуют установленным требованиям к точности, то есть такую АС действительно можно использовать для проведения в лаборатории рутинных исследований. Соответственно, воспользовавшись формулой (10.4), получим, что показатель S_i = 5*CVi/100 = 0,28 ммоль/л. Тогда, используя формулу (10.2), вычислим значение для показателя S_abv и получим:

S_abv = √(0,28*0,28+0,14*0,14) = √0,098 = 0,31 ммоль/л. Соответственно, используя формулу (10.3), для показателя CV_abv получим: CV_abv = √(5,6*5,6+2,75*2,75) = √38,6 = 6,24%. Из полученных данных для S_abv и CV_abv следует, что скорректированные результаты измерения уровня сывороточной глюкозы в последовательно взятых пробах здорового индивида, для которого гомеостатическая точка равна 5 ммоль/л, будут с 95% вероятностью попадать в интервал с границами 5+/–0,61 ммоль/л, то есть будут больше 4,39 ммоль/л , но меньше 5,61 ммоль/л. Границы этого интервала можно выразить и в процентах от уровня глюкозы в гомеостатической точке, что составит: 5 ммоль/л +/–12,2%. Но если в какой-то момент скорректированный текущий результат, полученный на такой АС, окажется меньше 4,39 ммоль/л или больше 5,61 ммоль/л, то тогда с 95% вероятностью можно утверждать, что появление такого результата уже нельзя объяснить аналитической и биологической вариациями уровня аналита. И скорее всего такой результат будет уже обуславливаться изменением состояния обследуемого пациента.

Примечание 10.5. Следует иметь в виду, что эксплуатационные значения систематического смещения и стандартного отклонения АС, как и измеренное значение уровня аналита, являются только приблизительными оценками их фактических значений. Как упоминалось в Лекции 3, эти оценки при необходимости можно использовать для вычисления границ доверительных интервалов, в которые попадают искомые фактические значения. Поэтому, если подставить в формулы (10.2) и (10.3) нижние и верхние границы таких доверительных интервалов, то можно получить оценки показателей S_abv и CV_abv как снизу, так и сверху, то есть получить оценку их максимально и минимально возможных значений.

Теперь перейдём к описанию алгоритмов сравнения результатов измерения уровня аналита в пробах с границами референтных диапазонов. Рассмотрим два типа таких диапазонов: индивидуальный и общепринятый межиндивидуальный. При рассмотрении первого типа будем полагать, что каждый здоровый индивид имеет свой персональный референтный диапазон с уникальными для него границами. При рассмотрении второго типа референтных диапазонов будем полагать, что его границы являются универсальными для всех здоровых индивидов с учетом их пола и возраста.

Возникший в последнее время интерес к первому типу референтных диапазонов обуславливается опытными данными, накопленными лабораторной и клинической медициной. Из этих данных следует, что каждый здоровый индивид имеет свою персональную гомеостатическую точку и свои персональные границы флуктуации уровня содержания аналита in vivo, которые с возрастом могут меняться. Интерес к индивидуальным референтным диапазонам продолжает расти [12], и, судя по всему, в ближайшее время перечисленные биологические параметры начнут определять персонально для каждого пациента. Как это уже делается для спортсменов путем внедрения персональных биологических паспортов. Вполне понятно, что границы индивидуальных референтных диапазонов для здорового индивида имеют прямую связь с внутрииндивидуальной биологической вариацией уровня исследуемого аналита. Если предположить, что уровни аналита в биожидкости здорового индивида in vivo распределены относительно своей гомеостатической точки в соответствии с нормальным законом, то можно оценить на 95% уровне доверия значения для нижней и верхней границ такого диапазона, определяя интервал, куда попадают 95% возможных значений исследуемого уровня аналита. Тогда значение нижней границы будет вычисляться как А_ниж = А_гт–1,96*S_i, а верхней как А_верх = А_гт+1,96*S_i, где S_i – стандартное отклонение внутрииндивидуальной биологической вариации, а A_гт – значение уровня аналита, соответствующее его гомеостатической точке.

Далее будут рассмотрены два алгоритма проведения сравнения скорректированных, то есть несмещенных относительно фактического значения, результатов измерений с границами индивидуального референтного диапазона, соответственно в зависимости от того, вышел результат за его пределы или нет.

Итак, сначала рассмотрим первый алгоритм. Если скорректированный результат измерения уровня аналита вышел за границы соответственного индивидуального референтного диапазона, то до тех пор, пока абсолютное значение (по модулю, то есть без учета знака) разности между ним и соответственно нижней А_ниж или верхней А_верх границей может объясняться аналитической вариацией измеряемого уровня аналита в пробах здорового индивида, то некорректно делать вывод, что уровень аналита в биожидкости in vivo обследуемого пациента вышел за пределы своей нормы. И наоборот, если скорректированный  результат отклонится в меньшую сторону от нижней или в большую сторону от верхней границы индивидуального референтного диапазона свыше некоторого предела, превысив критическое значение для таких разностей, что на выбранном уровне доверия уже нельзя объяснить только аналитической вариацией, то тогда и только тогда можно делать вывод, что уровень аналита в биожидкости обследуемого пациента in vivo вышел за пределы своей нормы. Но только на выбранном уровне доверия.

Теперь рассмотрим второй алгоритм. Если скорректированный результат измерения уровня аналита не вышел за границы индивидуального референтного диапазона, то до тех пор, пока абсолютное значение (по модулю) разности между ним и соответственно нижней А_ниж или верхней А_верх границей может объясняться аналитической вариацией измеряемого уровня аналита в пробах здорового индивида, то некорректно делать вывод, что уровень аналита в биожидкости in vivo обследуемого пациента находится в пределах своей нормы. И только если скорректированный результат, находясь внутри границ индивидуального референтного диапазона, отклонится в большую сторону от нижней границы или в меньшую сторону от верхней границы свыше некоторого предела, превысив критическое значение для таких разностей, что на выбранном уровне доверия уже нельзя объяснить только аналитической вариацией, то тогда и только тогда можно делать вывод, что уровень аналита в биожидкости обследуемого пациента in vivo находится в пределах своей нормы. Да и то, опять же, только на выбранном уровне доверия.

Для того, чтобы определить величины критической разницы, вспомним одно из свойств нормального распределения, из которого следует, что «несмещенные» результаты повторных измерений уровня аналита в одной и той же пробе вследствие их аналитической вариации могут отклоняться от своего генерального среднего как в большую, так и в меньшую сторону на величину Z*S_ac. Здесь, как и раньше, значение Z зависит от выбираемого уровня доверия и вида доверительного интервала для искомого фактического значения уровня аналита. Под генеральным средним в рассматриваемом случае будем понимать нижнюю или верхнюю границу индивидуального референтного диапазона. Обозначим искомое критическое значение разности между результатом и границами индивидуального референтного диапазона аббревиатурной RCV₁ (от Reference Change Value). Из вышеизложенного очевидным образом следует, что значения показателя RСV₁ должны вычисляться по следующей формуле:

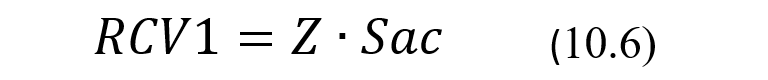
где Z – значение показателя Z-score, зависящее от выбираемого уровня доверия и вида доверительного интервала, в частности равное 1,96 для двустороннего доверительного интервала и выборе 95% уровня доверия. Для того, чтобы получить формулу для вычисления значений показателя относительной критической разницы, который далее будем обозначать как RСV₁(%), преобразуем формулу (10.6), умножая ее левую и правую стороны на 100 и деля каждую их них на скорректированный результат измерения Х_изм, и, соответственно, получим:

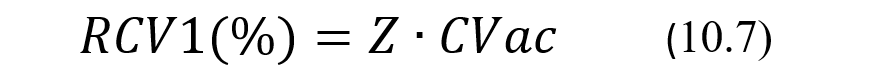
где показатель RCV₁(%) = 100*RCV₁/Х_изм, а показатель CV_ac = 100*S_ac/Х_изм

Несколько обобщим алгоритмы проведения сравнения результатов измерений с границами индивидуальных референтных диапазонов. Обозначим абсолютные значения (по модулю) разностей между скорректированным результатом Х_изм и границей диапазона, соответственно, как ∆_ниж = |Х_изм–А_ниж| и ∆_верх = |А_верх–Х_изм|. Относительные значения этих же разностей обозначим как ∆_ниж(%) = 100*|Х_изм–А_ниж|/Х_изм и ∆_верх(%) = 100*|А_верх–Х_изм|/Х_изм.

Тогда до тех пор, пока абсолютные или относительные значения этих разностей будут меньше соответственно показателя RCV₁ или показателя RCV₁(%), значения которых вычисляются по формулам (10.6) и (10.7), некорректно с выбранной доверительной вероятностью делать вывод, что уровень аналита в биожидкости обследуемого пациента in vivo вышел или не вышел за пределы своей нормы. Поскольку такое отличие результата измерения от соответствующей границы референтного диапазона вполне может объясняться его аналитической вариацией. И никаких других выводов делать тут нельзя. Если же при сравнении скорректированного результата измерения с границами индивидуального референтного диапазона он окажется ниже нижней или выше верхней границы, а его отличие от них превысит вычисленное критическое значение RCV₁ или RCV₁(%), то такое превышение уже нельзя будет объяснить только аналитической вариацией. И поэтому на выбранном уровне доверия можно будет считать, что уровень аналита in vivo является уже патологическим, делая вывод о произошедшем существенном изменении состояния обследуемого пациента. И, наконец, если скорректированный результат измерения окажется внутри границ референтного диапазона, а его отличие от них превысит вычисленное критическое значение RCV₁ или RCV₁(%), то такое превышение на выбранном уровне доверия будет показывать, что уровень аналита in vivo действительно находится в пределах своей нормы.

Примечание 10.6. Следует иметь в виду, что фактические значения уровня аналита in vivo могут на выбранном уровне доверия находиться в пределах своей нормы, несмотря на то что скорректированные значения результатов измерений уровня аналита оказываются вне границ индивидуального референтного диапазона, правда отклоняясь от них на величину не свыше значения RCV₁. И наоборот. Несмотря на то, что скорректированные значения результатов измерений оказываются внутри границ индивидуального референтного диапазона, отклонившись от них на величину не свыше значения RCV₁, соответствующие им фактические значения уровня аналита in vivo могут на выбранном уровне доверия быть уже патологическими, то есть фактически находиться за пределами своей нормы.

Примечание 10.7. Следует также иметь в виду, что вышеизложенные алгоритмы сравнения результатов измерений с границами индивидуальных референтных диапазонов можно будет использовать на практике только в случае предварительного получения данных о самих этих границах для конкретного индивида, когда его здоровье находится в норме. Краткие рекомендации по определению для здорового индивида оценочных значений гомеостатической точки А_гт и стандартного отклонения S_i внутрииндивидуальной биологической вариации содержания конкретного аналита в биожидкости in vivo изложены ниже в примечании 10.15. На основании полученных данных, значение нижней границы индивидуального референтного диапазона будет вычисляться как А_ниж = А_гт–1,96*S_i, а верхней – как А_верх = А_гт+1,96*S_i.

Поскольку типовые рекомендации по проведению таких исследований в виде стандарта пока не сформированы, то возможно это не позволит прямо сейчас начать широко использовать на практике такие алгоритмы. Тем не менее в самом ближайшем будущем следует ожидать появление такого стандарта, поскольку интерес к индивидуальным референтным диапазонам будет, по всей видимости, стремительно расти.

Теперь перейдем к рассмотрению алгоритмов сравнения результатов измерения уровня аналита с границами межиндивидуальных референтных диапазонов, также в зависимости от того, вышел ли результат за его пределы или нет. Отметим, что в справочниках представляются данные о границах именно таких диапазонов.

Сначала опишем, каким образом связаны между собой границы индивидуальных и межиндивидуальных референтных диапазонов. Исходя из вышеизложенного о природе внутрииндивидуальной биологической вариации вполне логично предполагать, что верхние и нижние границы межиндивидуальных референтных диапазонов представляют собой некие генеральные средние значения представительной совокупности соответственно верхних и нижних границ индивидуальных референтных диапазонов. С учетом, конечно, пола и возраста здоровых индивидов. В свою очередь, также можно предполагать, что верхние и нижние границы референтных диапазонов конкретных индивидов по всей видимости всегда в той или иной мере отличаются от соответствующих общепринятых границ, приводимых в справочниках, причем как в большую, так и в меньшую от них сторону. Тоже самое можно сказать и о гомеостатических точках конкретных индивидов. В том смысле, что у каждого индивида она имеет свое уникальное значение, а все вместе они образуют некую совокупность таких точек, распределенных определенным образом вокруг своего генерального среднего. В связи с вышеизложенным, стандартные отклонения S_g межиндивидуальных биологических вариаций уровней аналитов in vivo и их относительные значения в виде коэффициентов вариаций CV_g, именно которые и представляются обычно в соответствующих базах данных, например в [5], можно тогда рассматривать в качестве меры и для вариаций гомеостатических точек совокупности здоровых индивидов, и для вариаций границ индивидуальных референтных диапазонов. Предполагая нормальность таких распределений и используя соответствующие их свойства, можно также утверждать, что отклонения гомеостатических точек и соответствующих границ индивидуальных референтных диапазонов от своих генеральных средних как в большую, так и в меньшую сторону не превысит величины Z*S_g, где S_g – стандартное отклонение межиндивидуальной биологической вариации. Очевидно, что значения показателя CV_g, приводимые в широко известных базах данных по биологическим вариациям уровней аналитов in vivo, будут связаны со значениями показателя S_g следующим образом:

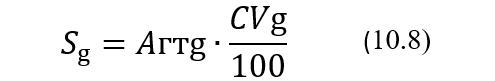
где A_гтg – уровень аналита, соответствующий некоей гомеостатической точке, усредненной по представительной выборке здоровых индивидов, и который в первом приближении можно равным середине межиндивидуального референтного диапазона, приводимого в справочниках.

Таким образом при проведении сравнения результатов измерений уровня аналита в пробах обследуемого пациента с границами межиндивидуального референтного диапазона следует иметь в виду, что относительно границ персонального референтного диапазона этого индивида они подвержены не только аналитической, но межиндивидуальной биологической вариации. Учет этого обстоятельства очень важен для адекватной оценки по результатам измерений фактического уровня аналита в биожидкости in vivo и его динамики. Поскольку из-за перечисленных выше вариаций результаты измерений уровня аналита в пробах даже здоровых пациентов вполне могут выходить за пределы границ межиндивидуального референтного диапазона. И наоборот, измеренные значения уровня аналита в пробах пациентов, у которых этот уровень in vivo фактически находится уже в области патологии, вполне могут по той же причине оказываться внутри границ межиндивидуального референтного диапазона.

После выяснения того обстоятельства, что при сравнении измеренных значений с границами межиндивидуальных референтных диапазонов необходимо также учитывать их аналитическую и межиндивидуальную биологическую вариацию, перейдем уже конкретно к рассмотрению самих алгоритмов.

Итак, во-первых, если скорректированный результат измерения вышел за границы межиндивидуального референтного диапазона, то до тех пор, пока его отличие от той или иной границы этого диапазона может объясняться суперпозицией аналитической и межиндивидуальной биологической вариации измеряемого уровня аналита в пробах здорового индивида, то некорректно делать вывод, что и уровень аналита в биожидкости обследуемого пациента in vivo тоже вышел за пределы своей нормы. Но если скорректированный результат, выйдя за границы такого диапазона, отклонится от его нижней или верхней границы свыше некоторого предельного для таких отклонений значения, что нельзя уже будет объяснить на выбранном уровне доверия только аналитической и межиндивидуальной биологической вариацией, то тогда можно делать вполне корректный вывод, что уровень аналита в биожидкости обследуемого пациента in vivo тоже вышел за пределы своей нормы. Но и то только на выбранном уровне доверия.

Теперь, во-вторых. Если скорректированный результат попадает внутрь межиндивидуального референтного диапазона, то до тех пор, пока его отличие от границ этого диапазона может объясняться суперпозицией аналитической и межиндивидуальной биологической вариаций, то некорректно на выбранном уровне доверия делать вывод, что и уровень аналита в биожидкости обследуемого пациента in vivo находится в пределах своей нормы. И только если скорректированный результат, находясь внутри границ межиндивидуального референтного диапазона, отклонится в большую сторону от нижней границы или в меньшую сторону от верхней границы свыше некоторого предельного для таких отклонений значения, что уже нельзя будет объяснить только аналитической и межиндивидуальной биологической вариацией, то тогда и только тогда можно делать корректный вывод о том, что и уровень аналита в биожидкости обследуемого пациента in vivo действительно находится в пределах своей нормы. Но только на выбранном уровне доверия.

Далее рассмотрим, каким образом надо определять вышеупомянутые предельные для отклонений значения, которые, как упоминалось выше, называют критическими разницами. Как и ранее, абсолютное значение (по модулю) текущей разницы между скорректированным результатом Х_изм и нижней границей А_ниж межиндивидуального референтного диапазона обозначим как ∆_ниж = |Х_изм–А_ниж|, а относительное – как ∆_ниж(%) = 100*|Х_изм–А_ниж|/Х_изм. Соответственно, абсолютное значение (по модулю) текущей разницы между скорректированным результатом Х_изм и верхней границей А_верх межиндивидуального референтного диапазона обозначим как ∆_верх = |Х_изм–А_верх|, а относительное – как ∆_верх(%) = 100*|Х_изм–А_верх|/Х_изм. Искомый показатель критической разности между скорректированными результатами и границами межиндивидуального референтного диапазона обозначим аббревиатурной RCV₂, происходящей, как уже упоминалось, от Reference Change Value. Соответственно, показатель относительной критической разности обозначим как RCV₂(%). Очевидно, что стандартное отклонение распределения вышеупомянутых текущих разностей ∆_ниж и ∆_верх для здоровых индивидов, которое мы обозначим как S_abv’, будет определяться суперпозицией аналитической и межиндивидуальной биологической вариаций. Также вполне понятно, что значения S_abv’ будут вычисляться на основе известного принципа сложения дисперсий, использованного ранее в формуле (10.2), по формуле:

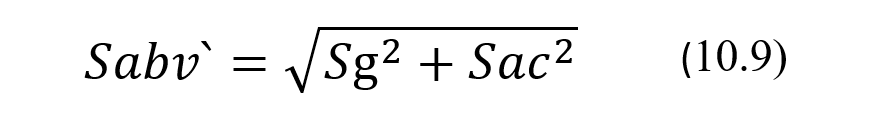
где S_g и S_ac – стандартные отклонения межиндивидуальной биологической и аналитической вариаций соответственно. Тогда, соответственно, значения для показателя критической разности RCV₂ будут вычисляться по вполне очевидной формуле:

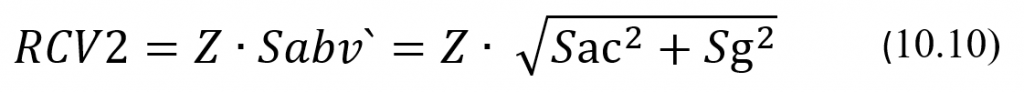
где Z – значение показателя Z-score, зависящее от выбираемого уровня доверия и вида доверительного интервала, в частности равное 1,96 для двустороннего доверительного интервала и выборе 95% уровня доверия.

Для того, чтобы получить формулу для вычисления значений показателя относительной критической разницы RCV₂(%), преобразуем соответствующим образом, как это будет показано ниже, формулу (10.10). Также будем иметь в виду, что показатели RCV₂(%) и RCV₂ связаны очевидно, как RCV₂(%) = 100*RCV₂/Х_изм, а показатели S_abv’ и CV_abv’ соответственно, как CV_abv’ = 100*S_abv’/Х_изм. Вспомним также, что CV_ac = 100*S_ac/Х_изм. И, наконец, из формулы (10.8) определим, что CV_g = 100*S_g/A_гтg, где A_гтg – уровень аналита, соответствующий некоей гомеостатической точке, усредненной по представительной выборке здоровых индивидов. Предположим также, что, как говорят, наилучшей оценкой для значения A_гтg будет результат измерения Х_изм. Хотя такая наилучшая оценка на самом деле может оказаться не совсем корректной, что соответствующим образом скажется на точности значений показателя RCV₂(%). Но выхода тут иного нет. Проведем, наконец, преобразование формулы (10.10), умножая ее левую и правую стороны на 100 и деля их на Х_изм, и тогда получим:

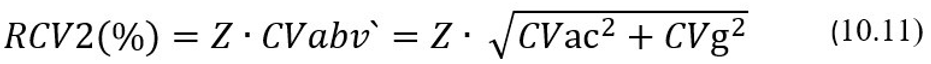
где CV_g и CV_ac – коэффициенты межиндивидуальной биологической и аналитической вариаций соответственно.

Таким образом можно констатировать, что до тех пор, пока абсолютное или относительное отличие скорректированного результата измерения от соответствующей границы межиндивидуального референтного диапазона – в большую или меньшую от нее сторону – меньше соответствующего показателя критической разницы RCV₂ или RCV₂(%), вычисляемых по формулам (10.10) или (10.11), то некорректно на выбранном уровне доверия делать какой-либо вывод о том, где в действительности находится уровень аналита в биожидкости обследуемого пациента in vivo по отношению к границам своей нормы. Он может находится как в пределах, так и за пределами своей нормы. Понятно, что причиной такой неопределенности являются аналитическая и биологическая вариации результатов измерений. Если же для какого-либо скорректированного результата измерения это абсолютное или относительное отличие превысит критическое значение RCV₂ или соответственно RCV₂(%), то такое превышение уже нельзя будет объяснить только наличием таких вариаций. Поэтому в случае, если такой скорректированный результат будет находиться вне границ референтного диапазона, то на выбранном уровне доверия следует считать, что уровень аналита in vivo действительно вышел за пределы своей нормы и делать вывод о произошедшем существенном изменении состояния обследуемого пациента. Соответственно, если скорректированный результат будет находиться внутри границ референтного диапазона, то на выбранном уровне доверия следует считать, что уровень аналита in vivo действительно находится в пределах своей нормы. Ниже рассмотрим конкретный пример сравнения с границами межиндивидуального референтного диапазона результатов, полученных на типовой АС для измерения уровней глюкозы в сыворотке, для чего проведем корректировку результатов на величину систематического смещения и вычислим для них соответствующее значение показателя RCV₂.

Пример 10.4. Воспользуемся одним из известных справочников и найдем значения для нижней и верхней границ межиндивидуального референтного диапазона для содержания глюкозы в сыворотке крови взрослых индивидов мужского пола. Предположим, что они оказались равны соответственно 4,1 ммоль/л и 5,9 ммоль/л. Соответственно, середина этого диапазона будет равна 5 ммоль/л. Вычислять значение показателя критической разницы RCV₂ будем для 95% уровня доверия по формуле (10.10). Значения АХ для типовой АС для измерения глюкозы в сыворотке крови возьмём из примера 10.2. Эта типовая АС имела следующие эксплуатационные значения для своих АХ: В_ас = +0,11 ммоль/л и S_ac = 0,14 ммоль/л, причём для всего диапазона измерений. Из базы данных [5] найдём что показатель CV_g для глюкозы в сыворотке равен 7,5%. Тогда используя формулу (10.8) получим, что S_g = 5ммоль/л*0,075 = 0,375 ммоль/л. И, наконец, используя формулу (10.10), вычислим значение для показателя критической разности RCV₂ для результатов, получаемых на такой АС, и получим, что RCV₂ = 0,79 ммоль/л. Тогда, в соответствии с вышеизложенными алгоритмами сравнения, все результаты измерений на такой АС, скорректированные на величину систематического смещения В_ас, которые будут меньше 4,1 ммоль/л и больше 3,3 ммоль/л, некорректно считать патологическими на 95% уровне доверия. Аналогично скорректированные результаты измерения, которые будут больше 5,9 ммоль/л и меньше 6,7 ммоль/л также нельзя на выбранном уровне доверия считать уже патологическими. И только те скорректированные результаты, которые окажутся меньше 3,3 ммоль/л или больше 6,7 ммоль/л можно будет на выбранном 95% уровне доверия считать уже точно патологическими. Особо отметим, что скорректированные результаты, которые будут больше 4,1 ммоль/л, но меньше 4,9 ммоль/л, а также те из них, которые будут больше 5,1 ммоль/л и меньше 5,9 ммоль/л, некорректно на 95% уровне доверия считать уже действительно нормальными. И только те скорректированные результаты, которые будут больше 4,9 ммоль/л и меньше 5,1 ммоль/л можно будет на выбранном 95% уровне доверия считать действительно нормальными.

Примечание 10.8. Следует иметь в виду, что на практике вполне возможны случаи, когда фактические значения уровня аналита in vivo могут на выбранном уровне доверия находиться в пределах своей нормы, несмотря на то, что скорректированные результаты измерений уровня аналита оказываются вне границ межиндивидуального референтного диапазона, правда отклоняясь от них на величину не свыше значения RCV₂. И наоборот, возможны случаи, когда скорректированные результаты измерений оказываются внутри границ межиндивидуального референтного диапазона, отклонившись от них на величину не свыше значения RCV₂, а соответствующие им фактические значения уровня аналита in vivo могут на самом деле быть уже патологическими, то есть фактически находиться за пределами своей нормы.

Примечание 10.9. Как следует из формул (10.6) и (10.10), значения показателей критических разностей RCV₁ и RCV₂ можно при необходимости уменьшать за счет увеличения кратности измерений уровня аналита в исследуемых пробах, о чем также шла речь в примечании 10.3 со ссылкой на формулу (10.5).

Вторая часть лекции будет посвящена алгоритмам сравнения между собой результатов измерения уровня аналита в пробах, последовательно взятых у одного и того же пациента. Также как и в первой части, которая была посвящена алгоритмам сравнения результатов измерений с границами референтных диапазонов, будет предполагаться, что для адекватной их интерпретации клиницистам следует сравнивать между собой уровни аналита, которые были у пациентов in vivo, а не in vitro, как это делается часто и сейчас.

Необходимость именно такого использования результатов в клинической практике возникает всегда, когда перед клиницистами стоит задача оценить динамику изменения уровня аналита у пациента из-за развития у него болезни или вследствие медикаментозного воздействия. И, как упоминалось ранее в этой лекции, с целью адекватной интерпретации полученных результатов при проведении такого сравнения необходимо учитывать не только возможную их аналитическую вариацию так сказать in vitro, но и биологическую вариацию уровня аналита в биожидкости пациента in vivo.

Прежде всего отметим, что в качестве базовой гипотезы во всех современных рекомендациях по использованию результатов измерений уровня аналита в пробах пациентов предполагается, что уровень исследуемого аналита в биожидкостях здоровых индивидов in vivo совершает колебания вокруг неких своих гомеостатических точек в определенных пределах и с определенной частотой, что в конечном итоге и обуславливает его биологическую вариацию для каждого конкретного индивида. Об этом же говорилось и в первой части этой лекции. Может быть, следует только добавить, что моменты достижения уровнем аналита своих гомеостатических точек, как и его значения в них, зависят от конкретного индивида и обычно априори неизвестны. Зато доподлинно известно, что вследствие изменений содержания аналита в биожидкостях in vivo, внутренне присущих человеческому организму, и природы измерительных процедур, результаты измерения уровня аналита в последовательно взятых пробах одного и того же здорового индивидуума будут всегда подвержены аналитической и биологической вариациям. Будем, как и ранее, предполагать, что представленные в справочниках показатели биологической вариации включают в себя и преаналитическую вариацию измеряемого уровня аналита, которую затруднительно выделить отдельно в процессе сбора или обработки экспериментальных данных. Таким образом, совокупность измеренных значений уровня аналита в пробах одного итого же здорового пациента будет представлять собой выборку элементов из распределения случайной величины, которое характеризуется дисперсией S_abv², а соответствующие значения S_abv вычисляют по формуле (10.2). Поскольку результаты такого исследования проб пациента, изначально предполагаемого здоровым, рассматриваются как случайные реализации уровня аналита в его гомеостатической точке in vivo, то при проведении сравнений текущего результата анализа с предыдущими в серии проб одного и того же пациента прежде всего необходимо проверить статистическую значимость их отличия. То есть, иными словами, необходимо проверить может ли величина разности текущего и предыдущего результатов еще объясняться их аналитической и биологической вариациями или уже нет. Для этого, по все видимости, надо сначала определить вид и параметры распределения разниц таких результатов.

С этой целью обозначим в виде последовательности Х_j (j = 1, 2, 3, …, n) результаты измерений уровня аналита в последовательно взятых пробах здорового пациента в количестве n. Значения разностей результатов Х_j+1 и  Х_j  измерения уровня аналита в двух последовательно взятых пробах будем вычислять по модулю, то есть без учета знака, обозначая их в виде показателя ∆_j = |Х_j+1 – X_j|. Распределение результатов измерений уровня аналита в пробах здорового индивида является, как об этом уже упоминалось ранее, практически нормальным. Из свойств нормальных распределений независимых случайных величин следует, что их разность тоже является случайной величиной, также распределенной по нормальному закону. Очевидно, что генеральное среднее разниц ∆_j будет равно нулю. Для определения дисперсии (S_∆)² разностей ∆_j воспользуемся известным свойством дисперсии, согласно которому дисперсия суммы или разности независимых случайных величин равна сумме их дисперсий, то есть равна сумме дисперсий текущих Х_j+1 и предыдущих Х_j результатов. Дисперсия каждого из этих результатов, как случайных величин, в свою очередь равна дисперсии S_abv². Тогда, используя формулу (10.2) для вычисления дисперсии S_abv², получим соответственно для определения дисперсии (S_∆)² разностей результатов измерения уровня аналита в двух последовательно взятых в пробах одного и того же здорового пациента следующую формулу:

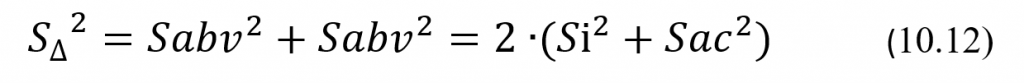
где S_i и S_ac – стандартные отклонения соответственно внутрииндивидуальной биологической и аналитической вариаций. Здесь, как и ранее, будем полагать, что эксплуатационное значение S_ac является константой для всего диапазона измерений используемой АС. Соответственно, для вычисления значений стандартного отклонения S_∆ разностей результатов измерения уровня аналита в двух последовательно взятых в пробах получим следующую формулу:

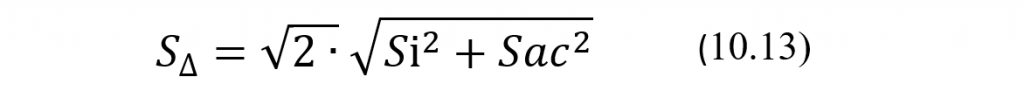
где S_ас – стандартное отклонение используемой АС, S_i – стандартное отклонение внутри-индивидуальной биологической вариации уровня исследуемого аналита, S_∆ – стандартное отклонение случайной величины ∆, которая представляет собой разность результатов измерений уровня аналита в двух последовательно взятых пробах здорового пациента, а ее текущие значения (по модулю) ∆_j вычисляются по формуле:

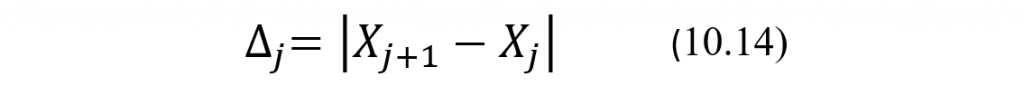
где Х_j+1 и Х_j – результаты измерения уровня аналита в двух последовательно взятых пробах одного и того же здорового пациента.

Примечание 10.10. Следует отметить, что рекомендации по использованию результатов измерений уровня аналита в пробах одного того же пациента особенно активно разрабатывались в последние десятилетия, главным образом для выявления существенных пре- и постаналитических ошибок, обусловленных, например, контаминацией или подменой проб. То есть скорее для оценки качества текущей работы лаборатории, чем для клинического применения. Рекомендации, по мере накопления опыта, совершенствовались и в конечном итоге это привело к созданию в 2006 году международного руководства CLSI EP33-Ed1 [9]. Это руководство содержит универсальные рекомендации по использованию в медицинских лабораториях так называемого метода Delta Checks, известного еще с 1974 года. Основная цель этого руководства заключается в том, чтобы предоставить лабораториям инструмент для выявления случаев появления «ненормальных» результатов в режиме текущего времени, дабы у них имелась возможность устанавливать причины такой «ненормальности» еще до выдачи результатов в клинику. В этом руководстве текущие результаты относятся к «ненормальным», если их отличие от предыдущих превышает некоторое заранее установленное критическое значение, зависящее от аналитической и биологической вариаций измеряемого уровня аналита. «Ненормальный» текущий результат рекомендуется передавать в клинику только тогда, когда по мнению лаборатории его «ненормальность» скорее всего объясняется существенным изменением состояния самого пациента. Тогда передача в клинику текущего результата совместно с информацией о его «ненормальности» позволит клиницистам легче выявлять у пациентов случаи запредельного изменения уровня аналита в биожидкостях in vivo.

Перейдем теперь к тому, каким образом следует определять критическое значение для разности между текущим и предыдущим результатами, при превышении которого текущий результат можно начинать считать уже «ненормальным». Для этого воспользуемся известным свойством нормального распределения, в соответствии с которым результаты Х_j измерений уровня аналита в последовательно взятых пробах здорового индивида будут отклоняться от своего генерального среднего значения А_гт на величину не свыше Z*S_abv, где А_гт – уровень исследуемого аналита в его гомеостатической точке, S_abv – стандартное отклонение распределения этих результатов, а Z – значение показателя Z-score, зависящее от выбираемого уровня доверия и вида доверительного интервала для текущего значения уровня аналита in vivo. Аналогичным образом будут вести себя и разности ∆_j = |Х_j+1–X_j| результатов измерения уровня аналита в двух последовательно взятых пробах такого же здорового индивида. То есть разности ∆_j = |Х_j+1 – X_j| будут отклоняться от своего математического ожидания, равного очевидно нулю, на величину не свыше Z*S_∆, где S_∆ – стандартное отклонение разностей результатов измерений уровня аналита в двух последовательно взятых пробах здорового индивида, которое вычисляется по формуле (10.13). Для оценки по выборочному среднему значению разниц ∆_j = |Х_j+1 – X_j| ее генерального значения следует по всей видимости использовать односторонний доверительный интервал, поскольку все значения разниц ∆_j в выборке берутся по модулю, то есть без учета их знака. Тогда, следуя данным, представленным в таблице 10.1, при выборе общепринятого 95% уровня доверия для случая одностороннего доверительного интервала показатель Z будет равен 1,65. Соответственно при выборе 90% и 99% уровня доверия значения Z для одностороннего доверительного интервала будут равны 1,28 и 2,33.

Примечание 10.11. В случае, если значения разниц ∆_j’ текущего и предыдущего результатов Х_j+1 и X_j определяются не по модулю, а с учетом их знака, то тогда для оценки по выборочному среднему значению разниц ∆_j’ = (Х_j+1 – X_j) ее генерального значения надо будет использовать двусторонний доверительный интервал, поскольку распределение разниц ∆_j‘ будет симметричным относительно своего генерального среднего. Тогда, следуя данным, представленным в таблице 10.1, при выборе общепринятого 95% уровня доверия для случая двустороннего доверительного интервала показатель Z будет равен 1,96. Соответственно, при выборе 90% и 99% уровня доверия значения Z для одностороннего доверительного интервала будут равны 1,65 и 2,58.

Тогда из вышеизложенного следует, что до тех пор, пока разности ∆_j = |Х_j+1–X_j| не превышают некоторое критическое для себя значение Z*S_∆, например, равное 1,65S_∆ для 95% уровня доверия, то отличие друг от друга рассматриваемых результатов на выбранном уровне доверия вполне объясняется внутри-индивидуальной биологической и аналитической вариациями измеряемого уровня аналита. В таких случаях, по всей видимости, следует полагать, что текущий и предыдущий результаты, с точки зрения оценки изменения состояния пациента, существенно не отличаются друг от друга и характеризуют стабильное его состояние.

Вышеизложенное позволяет сделать также и еще один вывод. Если в какой то момент времени разность текущего и предыдущего результатов превысит критическое для себя значение Z*S_∆, то тогда на выбранном уровне доверия такое их отличие уже нельзя будет объяснить только биологической и аналитической вариациями измеряемого уровня аналита. Такое их отличие будет обуславливаться, скорее всего, иными причинами, например ненормальным изменением содержания аналита in vivo вследствие изменения состояния здоровья у пациента. В таких случаях, скорее всего, следует полагать, что результаты, с точки зрения оценки состояния пациента, существенно отличаются друг от друга, что характерно для уже больного пациента. Именно поэтому величину Z*S_∆ называют критерием статистически значимого отличия результатов измерений в последовательно взятых пробах одного и того же пациента. Ее обозначают аббревиатурой RCV₃, также происходящей от выражения Reference Change Value. Достаточно часто эту величину также называют критерием критической разницы или просто показателем критической разницы, что тоже вполне адекватно отражает ее суть. Из вышеизложенного следует, что значения показателя RCV₃ вычисляются по нижеследующей формуле:

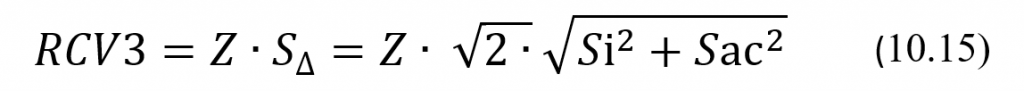
где Z – значение показателя Z-score, зависит от выбираемого уровня доверия и от вида доверительного интервала, используемого для оценки по выборочному среднему генерального значения разниц ∆_j = |Х_j+1–X_j|. При выборе 95% уровня доверия Z равно 1,65 в случае одностороннего доверительного интервала. Заметим, что в этой формуле значения показателя RCV₃ выражаются в тех же абсолютных единицах, в каких выражают результаты измерений и соответствующие им стандартные отклонения.

Особо отметим, что все вышесказанное справедливо только в условиях стабильности АХ АС и однотипности проведения преаналитических процедур. Тогда и только тогда при величине разности между текущим и предыдущим результатами измерения уровня аналита в пробах обследуемого пациента, превышающей показатель критической разности RCV₃, можно будет на выбранном уровне доверия утверждать, что фактический уровень аналита in vivo статистически значимо изменился вследствие изменения состояния пациента.

Примечание 10.12. В лабораторной медицине принято считать, что 95% уровень доверия позволяет делать выводы о статистически значимом изменении уровня аналита, а 99% уровня доверия – о высоком статистически значимом его изменении.

Чтобы получить возможность вычислять значения относительного показателя критической разницы RCV₃(%), преобразуем соответствующим образом формулу (10.15), как это описано чуть ниже в данном абзаце. Будем предполагать, что коэффициент аналитической вариации имеет одно и тоже значение для всего диапазона измерений АС, в том числе и для гомеостатической точки, то есть для уровня аналита, равного А_гт. Такое допущение позволит нам иметь следующее соотношение между стандартным отклонением S_ac и коэффициентом аналитической вариации С_ас: CV_ac = 100*Sac/А_гт. Тогда, умножая на 100 левую и правую стороны формулы (10.15) и деля их на величину уровня аналита в гомеостатической точке А_гт и, затем, заменяя стандартные отклонения на соответствующие коэффициенты вариации, получим следующую формулу:

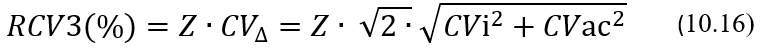
где RCV₃(%) = 100*RCV₃/А_гт, СV_∆ = 100*S_∆/А_гт, СV_i = 100*S_i/А_гт, CV_ac = 100*Sac/А_гт. Поскольку в настоящее время база данных по значениям А_гт даже для типовых аналитов еще не создана, то значение А_гт для того или иного аналита будем, как говорится, в первом приближении считать равным середине межиндивидуального референтного диапазона, приводимого в справочниках. При определении относительных разниц результатов ∆_j(%) в качестве оценки фактического значения уровня аналита в пробах вполне разумно использовать среднее значение Х_срj сравниваемых результатов, вычисляемое по формуле Х_срj = (Х_j+1+X_j)/2. Для простоты же можно также использовать для такой оценки и только первый или второй из сравниваемых результатов, как это предлагают делать K.Дж. Фразер в своей фундаментальной и широко известной работе [10] и авторы руководства EP33 [9]. Для однозначности выполним положения последних рекомендаций и будем оценивать фактическое значение по первому результату измерения Х_j. Тогда для вычислений относительных значений разности результатов получим следующую формулу:

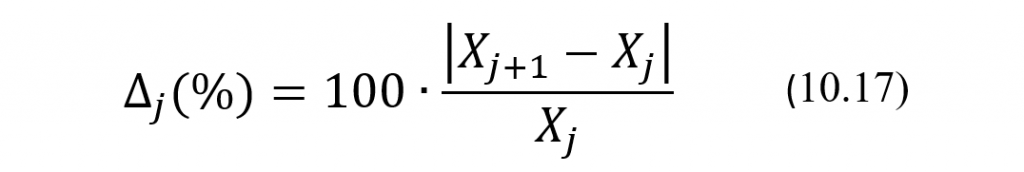
Тогда, если какое либо значение ∆_j(%), вычисленное по формуле (10.17), превысит значение RCV₃(%), вычисленное по формуле (10.16), то это будет свидетельствовать о статистически значимом различии сравниваемых результатов, которое на выбранном уровне доверия уже нельзя объяснить только их биологической или аналитической вариацией.

Примечание 10.13. В связи с необходимостью введения ряда допущений для вычислений показателя RCV3(%) по формуле (10.16), следует обязательно отметить, что более надежной проверкой на статистическую значимость отличия результатов является использование показателя критической разницы RCV₃, а не RCV₃(%).

Пример 10.5. Оценим на конкретном примере существенность отличия результатов измерения уровня аналита в двух последовательно взятых пробах одного и того же пациента. Предположим, что после проведения установочной серии на АС, используемой в лаборатории для измерения уровня глюкозы в сыворотке, ее эксплуатационные значения АХ оказались равными В_ас = +0,11 ммоль/л и S_ас = 0,14 ммоль/л. Будем предполагать, что значения смещения В_ас и коэффициента аналитической вариации CV_ac являются константами для всего диапазона измерений АС. Предположим также, что результаты измерения уровня глюкозы в двух последовательно взятых пробах пациента оказались равными Х₁ = 6,13ммоль/л и Х₂ = 6,85ммоль/л. Корректировать эти результаты на величину систематического смещения АС особого смысла нет, поскольку для сравнения с показателем RCV₃ используется их разность. Тем не менее для, так сказать, порядка, вычтем из каждого полученного результата 0,11 ммоль/л и получим после такой коррекции, что «несмещённые» результаты будут соответственно равны 6,02 ммоль/л и 6,74 ммоль/л. Разность ∆₁, равная |Х₂–Х₁|, и в том, и в другом случае, что мы и ожидали, будет равна ∆₁ = |Х₂–Х₁| = 0,72 ммоль/л. Соответственно, относительная разность ∆₁(%), вычисленная по формуле (10.17), будет равна ∆₁(%) = 100*|Х₂–Х₁|/Х₁ = 11,75%. Вполне понятно, почему абсолютные значения разности «оригинальных» и скорректированных результатов одинаковы. Но относительные значения этой разности будут отличаться вследствие изменения первого результата после коррекции (в данном случае это не так уж существенно). Далее рассчитаем по формулам (10.15) и (10.16) значения для показателей критической разности RCV₃ и RCV₃(%), выбирая общепринятый 95% уровень доверия и используя рекомендации EP33 [6] касательно оценки фактического значения по первому из двух рассматриваемых результатов измерения. Предварительно воспользуемся базой данных по биологическим вариациям уровней аналитов [5] и найдем, что коэффициент внутрииндивидуальной биологической вариации для уровня глюкозы в сыворотке равен CV_i = 5,6%. Сделаем также предположение, что уровень аналита A_гт, соответствующий его гомеостатической точке, равен середине референтного диапазона, приводимого в справочниках, то есть 5 ммоль/л. После этого, используя формулу (10.4), вычислим значение для показателя S_i и получим, что S_i = A_гт*CVi/100 = 5*5,6/100 ммоль/л = 0,28 ммоль/л. Воспользуемся формулой (10.15) и вычислим значение показателя RCV₃. Оно будет равно: RCV₃ = 1,65*1,414*√(0,28*0,28+0,14*0,14) = 0,74 ммоль/л. Затем, используя формулу (10.16), вычислим значение показателя RCV₃(%). Проводя расчеты вспомним о нашем допущении, что CV_ac = 100*Sac/А_гт, и определим, что для данного конкретного примера показатель CV_ac будет 100*0,14/5 = 2,8%. Воспользуемся полученным значением CV_ac и вычислим значение показателя RCV₃(%): RCV₃(%) = 1,65*1,414*√(5,6*5,6+2,8*2,8) = 14,61%. Поскольку разность ∆₁, равная 0,72 ммоль/л, оказалась меньше критического значения RCV₃, равного 0,74 ммоль/л, то отсюда следует, что результаты Х₁ = 6,13 ммоль/л и Х₂ = 6,95 ммоль/л не отличаются статистически значимо друг от друга. То есть оба рассматриваемых результата с 95% вероятностью имеют отношение к одному и тому же здоровому индивиду, а такое на первый взгляд немалое отличие этих результатов объясняется их аналитической и биологической вариациями. И аналогично, поскольку относительное значение разности двух результатов ∆₁(%), равное 11,75%, оказалось меньше значения RCV₃(%), равного 14,61%, то и отсюда также следует, что результаты Х₁ = 6,13 ммоль/л и Х₂ = 6,95 ммоль/л существенно друг от друга не отличаются с точки зрения оценки состояния обследуемого пациента.

Примечание 10.14. Вопросы определения существенности отличия результатов повторных измерений уровня аналита в одной и той же биопробе достаточно часто возникают и у врачей клинической лабораторной диагностики при ведении ВКК с использованием контрольных материалов (далее – КМ). В последнем случае нет необходимости при проведении сравнения результатов учитывать помимо аналитической еще и биологическую вариацию уровня аналита. Хотя и здесь есть свои нюансы. Так, например, в общем случае при сравнении результатов анализа образцов КМ возникает необходимость учитывать их происхождение. И если анализируемые образцы являются аликвотами, произошедшими не из одного и того же флакона КМ, а из разных, то тогда при интерпретации результатов надо будет вместо биологической вариации учитывать возможную вариацию содержания аналита во флаконах одного и того же лота. Соответственно, если заменить в предыдущих формулах показатели биологической вариации уровня аналита на межфлаконные, то тогда все эти формулы можно будет использовать для определения существенности отличия результатов повторных измерений уровня аналита в образцах КМ из разных флаконов одного и того же лота. В случае, если в паспорте изготовителя КМ нет информации о межфлаконной вариации, то тогда лаборатория самостоятельно должна оценить разброс уровня аналита между флаконами одного и того же лота. Для этого надо использовать выборку хотя бы из 10 флаконов, взятых наугад, и затем определить стандартное отклонение и коэффициент межфлаконной вариации уровня аналита на основе данных одной серии.

Чтобы можно было использовать приведенные ранее формулы для оценки существенности различия результатов повторных измерений уровня аналита в аликвотах, происходящих из одного и того же флакона КМ, несколько их упростим, убирая показатели биологической вариации. В итоге для вычисления основных показателей получим нижеследующие формулы:

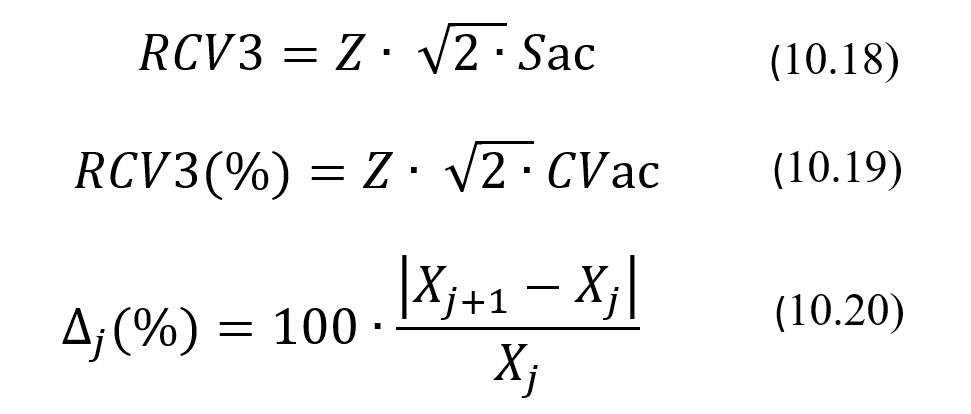
Примечание 10.15. Для того чтобы оценить для здорового индивида значение гомеостатической точки и стандартного отклонения S_i внутрииндивидуальной биологической вариации содержания конкретного аналита в биожидкости invivo необходимо провести серию измерений уровня этого аналита в пробах, последовательно взятых у этого индивида в течение периода полного колебания. Эти пробы – в статистически значимом количестве, то есть не менее 20, – надо будет брать у обследуемого индивида через промежутки времени, существенно более короткие, чем длительность полного цикла колебаний уровня исследуемого аналита вокруг его гомеостатической точки. Затем на базе полученных результатов по аналогии с установочной серией вычисляются по известным формулам их среднее значение Х_ср, которое будет являться оценкой уровня аналита в его гомеостатической точке, и их стандартное отклонение S_abv. Для оценки уровня аналита Агт в его гомеостатической точке следует очевидно использовать формулу:

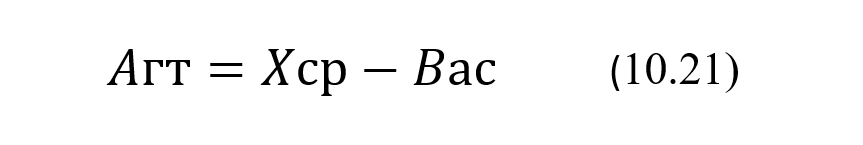
а для оценки показателя S_i нижеследующую формулу, полученную путем преобразования формулы (10.2):

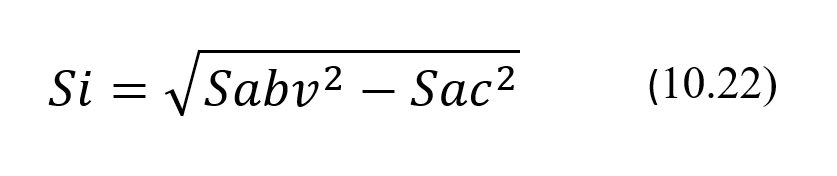
где В_ас – систематическое смещение используемой АС, S_abv – стандартное отклонение результатов измерения уровня аналита в пробах, последовательно взятых у одного и того же здорового индивида, S_i и S_ac – стандартные отклонения внутрииндивидуальной биологической и аналитической вариаций соответственно.

В последней, третьей, части лекции рассмотрим еще несколько типовых практических ситуаций и задач, возникающих очень часто в медицинских лабораториях, для решения которых требуется оценка статистической значимости отличия двух результатов последовательных измерений.

Пример 10.6.

Типовая ситуация 1. У сотрудников лаборатории начало создаваться впечатление, что результаты, получаемые на одной из АС, «скачут» в течение одного дня. Это произошло после того, как на этой АС в одной аналитической серии был измерен уровень в двух аликвотах одной и той же пробы и получены результаты Х₁ и Х₂. Сотрудники непосредственно сравнили между собой два этих результата и обнаружили, что они несколько отличаются друг от друга, то есть «не совпадают». Тогда они задумались, каким образом убедиться, что полученные результаты действительно «не совпадают», то есть как убедиться, что они существенно отличаются друг от друга? То есть, что их отличие обусловлено не только их аналитической вариацией?

Предлагаемый алгоритм решения. Чтобы обоснованно ответить на этот вопрос помимо самих результатов Х₁ и Х₂ дополнительно потребуются значения коэффициента аналитической вариации и показателя критической разницы, которые соответствуют сути решаемой задачи. Поскольку измерения проводились в одной аналитической серии в аликвотах одной и той же пробы, то очевидно, что показатель CV_i следует в данном случае считать равным нулю, а при оценке существенности отличия полученных результатов следует использовать коэффициент внутрисерийной вариации (CV_ac)_w. Этот показатель характеризует количественно повторяемость результатов. На его основе и будет вычисляться значение показателя RCV_3w(%) по формуле (10.16), то есть следующим образом: RCV_3w(%)=√2*Z*(CV_ac)_w. Упомянутое значение (CV_ac)_w можно определить, либо используя данные установочной серии, либо получив необходимые данные заново, проведя серию из, например, 10 измерений уровня аналита в аликвотах одной и той же пробы. И тогда, если вычисленное по формуле (10.17) относительное значение разности полученных результатов ∆₁(%) = 100*|Х₂–X₁|/Х₁ окажется на выбранном уровне доверия больше показателя RCV_3w(%), то это будет указывать на статистически значимое отличие полученных результатов, которое нельзя объяснить только их аналитической вариацией. То есть на то, что результаты действительно «не совпадают». В противном случае отличие результатов на выбранном уровне доверия вполне будет объясняться измерительными свойствами используемой АС. Обычно для решения таких задач выбирают 95% уровень доверия и односторонний доверительный интервал для оценки генерального среднего искомой относительной разности результатов. Поэтому значение Z для показателя Z-score следует брать равным 1,65.

Конкретный рабочий случай. Было определено, что АС, используемая лаборатории для измерения уровня глюкозы в сыворотке, имеет коэффициент внутрисерийной вариации (CV_ac)_w, равный 1,5%. На этой АС в одной из аналитических серий измерили уровень глюкозы в двух аликвотах одной и той же пробы и получили результаты Х₁ = 6,2 ммоль/л и Х₂ = 5,9 ммоль/л, после чего возник вопрос относительно статистической значимости их отличия. Для ответа на этот вопрос был выбран 95% уровень доверия и вычислено относительное значение показателя критической разницы, которое оказалось равным RCV_3w(%) = √2*Z*(CV_ac)_w = 1,414*1,65*1,5% = 3,5%, а также относительное значение (по модулю) разности полученных значений, которое оказалось равным ∆₁(%) = 100*|Х₂–X₁|/Х₁ = 100*|5,9–6,2|/6,2 = 4,84%.

Вывод. Поскольку относительная разность ∆₁(%) оказалась больше показателя критической разницы RCV_3w(%), то отсюда следует, что на 95% уровне доверия полученные в серии результаты измерения уровня аналита в аликвотах одной и той же пробы отличаются статистически значимо. Такое отличие нельзя объяснить только их аналитической вариацией, то есть только измерительными свойствами используемой АС. Таким образом результаты, получаемые на данной АС, действительно в течение одного дня «скачут».

Пример 10.7.

Типовая ситуация 2. У сотрудников лаборатории начало создаваться впечатление, что результаты измерения аналита в аликвотах одной и той же пробы, полученные на АС в разные дни, отличаются друг от друга, то есть «скачут» изо дня в день. Тогда они задумались о том, каким образом объективно убедиться, что полученные в разных сериях результаты Х₁ и Х₂ действительно «не совпадают», то есть, что они существенно отличаются друг от друга? То есть как убедиться в том, что отличие этих результатов обусловлено не только их межсерийной аналитической вариацией?

Предлагаемый алгоритм решения. Чтобы ответить на этот вопрос помимо самих результатов Х₁ и Х₂ дополнительно потребуются значения для коэффициента аналитической вариации для показателя критической разницы, которые соответствуют сути решаемой задачи. Поскольку измерения проводились в разные дни, то для вычисления значения показателя критической разницы понадобится коэффициент межсерийной вариации CV_ac, характеризующий количественно прецизионность результатов, получаемых на данной АС. Поскольку измерения проводились в аликвотах одной и той же пробы, то, очевидно, показатель CV_i следует считать равным нулю. Поэтому вычислять относительное значение показателя критической разницы надо будет по несколько упрощенной формуле (10.16), в которой CV_i = 0: RCV₃(%) = √2*Z*CV_ac. Упомянутое значение CV_ac для используемой АС можно получить или на основе данных установочной серии, или определить заново. Тогда, если вычисленное по формуле (10.17) относительное значение разности полученных результатов ∆₁(%) = 100*|Х₂–X₁|/Х₁ окажется на выбранном уровне доверия больше вычисленного значения показателя RCV₃(%), то это будет указывать на статистически значимое отличие результатов, которое нельзя объяснить только их аналитической вариацией. В противном случае отличие результатов на выбранном уровне доверия вполне будет объясняться измерительными свойствами используемой АС. Обычно для решения таких задач выбирают 95% уровень доверия и односторонний доверительный интервал для оценки генерального среднего относительной разности результатов. Поэтому значение Z для показателя Z-score следует выбирать равным 1,65.

Конкретный рабочий случай. Для АС, используемой в лаборатории для измерения уровня глюкозы в сыворотке, ранее было определено значение коэффициента межсерийной вариации CV_ac, которое оказалось равным 2,5%. На этой АС в разные два дня измерили уровень глюкозы в аликвотах одной и той же пробы и получили результаты Х₁ = 6,2 ммоль/л и Х₂ = 5,9 ммоль/л, после чего возник вопрос относительно статистической значимости такого их отличия. Для ответа на него был выбран 95% уровень доверия и затем вычислено относительное значение показателя критической разницы, которое оказалось равным RCV₃(%) = √2*Z*CVac = 1,414*1,65*2,5%=5,83%, и относительное значение (по модулю) разности ∆₁(%) =100*|Х₂–X₁|/Х₁ = 100*|5,9-6,2|/6,2 = 4,84%.

Вывод. Поскольку относительная разность ∆₁(%) оказалась меньше показателя критической разницы RCV₃(%), то отсюда следует, что на 95% уровне доверия результаты измерения уровня аналита в одной и той же пробе, но полученные в разных аналитических сериях, не отличаются статистически значимо друг от друга. Такое отличие вполне объясняется их аналитической вариацией, то есть измерительными свойствами используемой АС. И таким образом результаты, получаемые на данной АС, на самом деле изо дня в день не «скачут».

Пример 10.8.

Типовая ситуация 3. У сотрудников лаборатории создалось впечатление, что результаты измерения аналита в пробах одного и того же пациента, полученные на двух разных АС, заметно отличаются друг от друга. Тогда они задумались о том, каким образом объективно убедиться, что результаты Х₁ и Х₂ измерения аналита в пробах одного и того же пациента, но полученные на разных АС, существенно отличаются друг от друга? То есть как убедиться в том, что отличие результатов обусловлено не только их аналитическими вариациями, то есть не только измерительными свойствами используемых АС?

Предлагаемый алгоритм решения. Чтобы ответить на этот вопрос помимо самих результатов Х₁ и Х₂ дополнительно потребуются данные о систематических смещениях и коэффициентах вариаций обеих АС, а также значение внутри индивидуальной биологической вариации CV_i и относительное значение показателя критической разницы, которое соответствует сути решаемой задачи. Поскольку измерения проводились на разных АС, то для вычисления значений показателя критической разницы понадобятся коэффициенты межсерийной вариации CV_ac1 и CV_ac2, характеризующие количественно прецизионность результатов, получаемых соответственно на первой и на второй АС. На их основе и будет вычисляться относительное значение показателя RCV₃(%), причем по более усложненной формуле, чем формула (10.16), а именно: RCV₃(%) = Z*√(CV_i²+CV_aс1²+CV_i²+CV_aс2²), так как измерения проводились на разных АС в разных пробах, хотя и взятых у одного и того же пациента. Тогда, если вычисленное по формуле (10.17) относительное значение разности «несмещенных» результатов ∆₁(%) = 100*|Х₂–В_ас2–X₁–В_ас1|/(Х₁–В_ас1), где В_ас1 и В_ас2 – систематические смещения соответственно первой и второй АС, окажется на выбираемом уровне доверия больше значения показателя RCV₃(%), то это будет указывать на статистически значимое отличие результатов, которое нельзя объяснить только их аналитической вариацией. В противном случае отличие результатов на выбранном уровне доверия будет вполне объясняться измерительными свойствами используемых АС. Обычно для решения таких задач выбирают 95% уровень доверия и односторонний доверительный интервал для оценки математического ожидания относительной разности результатов. Поэтому значение Z для показателя Z-score следует выбирать равным 1,65.

Конкретный рабочий случай. Для каждой из двух АС, используемых в лаборатории для измерения уровня глюкозы в сыворотке, ранее были определены значения коэффициентов межсерийной вариации CV_ac1 и CV_ac2, которые оказались равными соответственно 2,5% и 2,8%, и значения систематических смещений В_ас1 и В_ас2, которые оказались равными +0,15 ммоль/л и 0,12 ммоль/л соответственно. Коэффициент внутрииндивидуальной биологической вариации для глюкозы в сыворотке, как следует из [5], равен CV_i = 5,6%. Результаты измерений уровня глюкозы в сыворотке на первой и второй АС оказались равными соответственно Х₁ = 6,5 ммоль/л и Х₂ = 5,9 ммоль/л, после чего и возник вопрос относительно статистической значимости такого их отличия. Для ответа на этот вопрос был выбран 95% уровень доверия и затем вычислено относительное значение показателя критической разницы, которое оказалось равным RCV₃(%) = Z*√(2*CV_i²+CV_aс1²+CV_aс2²) = 1,65*√(2*5,6*5,6+2,5*2,5+2,8*2,8) = 1,65*8,76% = 14,46%. Затем было вычислено относительное значение разности несмещенных результатов, которое оказалось равным ∆₁(%) = 100*|Х₂–В_ас2–X₁–В_ас1|/(Х₁–В_ас1) = 100*|5,9–0,15–6,5+0,12|/(6,5+0,12) = 9,52%.

Вывод. Поскольку относительная разность ∆₁(%) оказалась меньше показателя критической разницы RCV₃(%), то отсюда следует, что на 95% уровне доверия полученные на разных АС результаты измерения уровня глюкозы в пробах одного и того же пациента не отличаются статистически значимо друг от друга. Их отличие вполне объясняется аналитическими характеристиками используемых АС и биологической вариацией уровня аналита in vivo. Таким образом, результаты, получаемые на данных АС, на самом деле заметно друг от друга не отличаются.

Пример 10.9.

Типовая ситуация 4. У сотрудников лаборатории создалось впечатление, что результаты измерения уровня аналита в пробах одного и того же стабильного пациента «сильно отличаются». Это было связано с тем, что проанализировали разные пробы одного и того же стабильного пациента, взятые в разные дни, и получил результаты Х₁ и Х₂, которые по их представлениям чрезмерно отличаются друг от друга. Тогда они задумались о том, каким образом можно объективно убедиться, что результаты Х₁ и Х₂ измерения аналита в пробах одного и того же пациента действительно значимо отличаются друг от друга, что нельзя объяснить их аналитической и биологической вариациями, либо их отличие находится в пределах, так сказать, статистической ошибки, обусловленной измерительными свойствами используемой АС и индивидуальной биологической вариацией уровня аналита in vivo?

Предлагаемый алгоритм решения. Чтобы ответить на этот вопрос помимо самих результатов Х₁ и Х₂ дополнительно потребуются значения коэффициента аналитической вариации и показателя критической разницы, которые соответствуют сути решаемой задачи. Поскольку измерения проводились в разные дни, то для вычисления значения показателя критической разницы понадобится коэффициент межсерийной вариации CV_ac, характеризующий количественно прецизионность результатов, получаемых на данной АС, и коэффициент внутрииндивидуальной биологической вариации CV_i. Вычислять относительное значение показателя RCV₃(%) надо будет, что вполне понятно, по формуле (10.16): RCV₃(%) = √2*Z*√(CV_i²+CV_ac²). Упомянутое значение CV_ac для используемой АС можно получить или на основе данных установочной серии, либо определить заново. Тогда, если вычисленное по формуле (10.17) относительное значение разности полученных результатов ∆₁(%) = 100*|Х₂–X₁|/Х₁ окажется на выбранном уровне доверия больше показателя RCV3(%), то это будет указывать на статистически значимое отличие результатов, которое нельзя объяснить только их аналитической и биологической вариациями. В противном случае отличие результатов на выбранном уровне доверия будет объясняться измерительными свойствами используемой АС и биологической вариацией уровня аналита in vivo. Обычно для решения таких задач выбирают 95% уровень доверия и односторонний доверительный интервал для оценки генерального среднего относительной разности результатов. Поэтому значение Z для показателя Z-score следует выбирать равным 1,65.

Конкретный рабочий случай. Для АС, используемой в лаборатории для измерения уровня глюкозы в сыворотке, ранее было определено значение коэффициента межсерийной вариации CV_ac, которое оказалось равным 2,8%. Коэффициент внутрииндивидуальной биологической вариации для глюкозы в сыворотке, как следует из [5], равен CV_i = 5,6%. На этой АС измерили уровень глюкозы в пробах одного и того же пациента, взятые в разные дни, и получили результаты Х₁ = 6,5 ммоль/л и Х₂ = 6,1 ммоль/л, после чего возник вопрос относительно статистической значимости такого их отличия. Для ответа на него был выбран 95% уровень доверия и затем вычислено значение показателя критической разницы, которое оказалось равным RCV₃(%) = √2*Z*√(CV_i²+CV_ac²) = 1,414*1,65*√(5,6*5,6+2,8*2,8) = 14,61%, и относительное значение разности ∆₁(%) = 100*|Х₂–X₁|/Х₁ = 100*|6,1-6,5|/6,5 = 6,15%.

Вывод. Поскольку относительная разность ∆₁(%) оказалась меньше показателя критической разницы RCV₃(%), то отсюда следует, что на 95% уровне доверия результаты измерения уровня аналита в пробах одного и того же пациента в разные дни не отличаются статистически значимо друг от друга. Такое отличие вполне объясняется их аналитической вариацией, обусловленной измерительными свойствами используемой АС и внутрииндивидуальной биологической вариацией уровня аналита in vivo. Таким образом результаты, получаемые на данной АС, на самом деле заметно друг от друга не отличаются.

Краткие выводы по Лекции 10.

1. Все результаты измерений уровней аналитов в пробах пациентов содержат ошибки, максимальные размеры которых определяются аналитическими характеристиками используемых аналитических систем, в связи с чем лабораторные результаты всегда отличаются от своих фактических значений то в меньшую, то в большую сторону.
2. Содержание практически всех аналитов in vivo не остаётся постоянным, поскольку подвержено внутри индивидуальным биологическим вариациям, обусловленным физиологическими процессами, происходящими в человеческом организме. Уровни аналитов в биожидкостях здоровых индивидов in vivo флуктуируют с характерной для них частотой вокруг своих так называемых гомеостатических точек.
3. В этой связи при сравнении результатов измерений уровня аналита в пробах пациента между собой и с границами референтных диапазонов нельзя делать выводы только на основе измеренных значений. Для адекватной интерпретации полученных результатов необходимо также учитывать и возможную биологическую вариацию содержания аналита in vivo, и возможную аналитическую вариацию результатов.
4. При сравнении результатов повторных измерений уровня аналита в образцах (флаконах) контрольного материала одного и того же лота необходимо учитывать возможную аналитическую вариацию полученных результатов и вариацию содержания аналита между флаконами.
5. Обычно статистически значимое отличие результатов измерения уровня аналита в пробах пациента как друг от друга, так и от границ референтного диапазона, принято выявлять с использованием так называемого показателя критической разницы RСV, значения которого определяются и биологической, и аналитической вариациями. Если отличие текущего результата от предыдущего превышает соответствующее значение RCV, то такое отличие считается статистически значимым, поскольку его уже нельзя объяснить только биологической и аналитической вариациями. Если отличие результата от другого или от границы нормы меньше соответствующего значения RCV, то такое отличие не считается существенным, поскольку вполне объясняется биологической и аналитической вариациями.

Литература к Лекции 10.

1. Mario Plebani. «Errors in clinical laboratories or errors in laboratory medicine?» Clin Chem Lab Med 2006; 44(6): 750–759, 2006.

2. Kalra J. «Medical errors: impact on clinical laboratories and other critical areas» Clin Biochem 2004; 37:1052–62.

3. Cotlove E., Harris E.K., Williams G.Z. Biological and analytic components of variation in long-term studies of serum constituents in normal subjects III. Physiological and medical implications. Clinical Chemistry, Volume 16, Issue 12, 1 December 1970, pp 1028–1032.

4. Harris E.K., Kanofsky P., Shakarji G., Cotlove E. Biological and analytic components of variation in long-term studies of serum constituents in normal subjects II. Estimating biological components of variation. Clinical Chemistry, Volume 16, Issue 12, 1 December 1970, Pages 1022–1027.

5. https://www.westgard.com/biodatabase1.htm

6. Aarsand, AK, Webster, C, Coskun, A, Gonzales-Lao, E, Diaz-Garzon, J, Røraas, T, et al. EFLM biological variation database. Available from: https://biologicalvariation.eu

7. Carobene, A, Aarsand, A.K, Bartlett, W.A, Coskun, A, Diaz-Garzon, J et al. The European Biological Variation Study (EuBIVAS): summary report. Clin Chem Lab Med 2022;60:505–517.

8. Tony Badrick. Biological variation: Understanding why it is so important? Practical Laboratory Medicine, vol 23, January 2021.

9. Clinical and Laboratory Standards Institute «Use of Delta Checks in the Medical Laboratory». CLSI Guideline — 1st Edition. CLSI Document EP33. CLSI catalog: Vol. 36, No. 3, 2006.

10. Callum G. Fraser. “Biological variation: From Principles to Practice”. AACC Press, 2001.

11. J.H.Koeslag, P.T.Saunders, E.Terblanche. Reappraisal of the Blood Glucose Homeostat which Comprehensively Explains the Type 2 Diabetes Mellitus-Syndrome X Complex. The Journal of Physiology v 549 issue 2 pp 333-346, June 1, 2003.

12. Coş kun A, Sandberg S, Unsal I, Cavusoglu C, Serteser M, Kilercik M, et al. Personalized reference intervals in laboratory medicine: a new model based on within-subject biological variation. Clin Chem. 2021;67:374-384.

---

Скачать Лекцию 10